时变地震子波提取研究方法综述

戴永寿,张彧豪,张 鹏,张红倩,王春娴

(中国石油大学(华东)海洋与空间信息学院,山东青岛266580)

随着油气勘探目标埋深和复杂程度的加大,地震流体识别难度也在不断加大,这对地震剖面的分辨率及反演解释的精确度提出了更高要求。由于地震介质对地震波能量的吸收衰减作用,造成子波高频成分缺失和相位畸变,从而使子波表现出时变特性。以往的地震子波提取方法往往基于子波时不变的假设,因此提取出的子波无法满足地震勘探所需的精度要求。尚新民等[1]利用时不变子波和时变子波分别对实际地震资料进行处理,结果利用时变子波处理的地震数据分辨率更高、有效频带更宽;李振春等[2]在S域利用时变子波与地震记录进行反褶积,使地震剖面的同相轴变细且连续性变好,浅、中、深层的能量都得到了补偿,且深层能量改善明显;迟唤昭等[3]也指出,相对前人采用的非时变子波,采用时变子波作谱反演处理后的地震剖面分辨率更高。故时变地震子波的提取是目前高分辨率地震资料处理方法的研究重点之一。目前从非平稳地震记录中提取时变地震子波的方法主要有两类:一类是先对非平稳地震记录进行衰减补偿或分段处理,使其整体或每段近似成为平稳地震记录,然后采用常规方法提取地震子波;另一类是从非平稳地震记录中提取子波振幅谱与相位谱,再将二者匹配融合从而提取时变地震子波。本文主要概括了近年主流的时变地震子波提取方法,对每种方法的原理、优缺点和适用条件进行了分析,并对地震子波提取方法的研究前景进行了展望。

1 基于衰减补偿和分段处理的子波提取方法

实际地震资料中的地震子波具有时变特征,即地震资料具有非平稳性[4]。对非平稳地震记录进行衰减补偿或分段处理,使其整体或分段成为近似平稳地震记录,然后结合常规方法提取地震子波的方法成为目前时变地震子波提取的研究方向之一。

1.1 衰减补偿方法

随着对地下介质研究的深入,关于大地对地震波的吸收机理研究目前存在多种理论[5],主要包括Biot理论和喷射流动理论、散射、电化学作用和毛细管作用、岩石颗粒间的摩擦滑移等。地震波在地层中的衰减和频散一般可以用经验公式来表示,国内外学者建立了Power Law模型、Kjartansson模型、Kolsky-Futterman模型、Müller模型等多种模型,其中Kolsky-Futterman模型能更好地描述地震波在地下介质中的传播规律且简单方便,在子波的衰减补偿中被广泛应用。该模型中Q值基本上不随频率变化,可以看作恒Q模型。

目前发展比较成熟的衰减补偿方法主要包括:谱白化方法、反Q滤波方法、时频域衰减补偿方法和多尺度联合分析方法等,本节对上述主流方法的优缺点进行了概述。由于多尺度联合分析方法依赖测井资料,无法对整个地震记录进行补偿,谱白化方法基于反射系数序列是白噪的假设,在实际应用中具有较大的限制,故在此均不作过多论述。

1.1.1 反Q滤波方法

地震波经地层传播后能量被损耗,高频部分衰减严重,此时可将大地看作一个低通滤波器,此过程被称为Q滤波。反Q滤波是Q滤波的反过程,是针对地层的低通滤波特性,对地震数据进行的补偿处理。目前反Q滤波方法已经较为成熟,但仍存在以下两方面问题:①反Q滤波的准确度很大程度取决于Q值的求取,而Q值往往难以精确求取;②目前计算效率高的反Q滤波方法都假设地下介质是一个常Q或者层状Q模型,这并不能反映地下介质的真实情况[6]。

1.1.2 时频域衰减补偿方法

谱白化方法、反Q滤波方法和多尺度联合分析方法由于各自的缺陷在非平稳地震记录高频补偿中的应用均受到了一定限制,近年来,专家和学者又提出了许多新的补偿方法。其中时频分析方法因其可以同时联合时间域和频率域信息对信号进行处理,克服了傅里叶变换时域和频域完全分离的缺陷,成为目前地震资料处理的有力工具。但此类方法在对地震记录做衰减补偿时假设地震记录的低频成分是近似不衰减的,与实际情况不符[7]。MARGRAVE等[8]在Gabor域进行衰减补偿和反褶积以估计地层的反射系数,补偿了中、深层的能量衰减并因此拓宽有效频带和提高时间分辨率,但在地层衰减剧烈时,此方法效果不理想。常用的时频分析方法还有短时傅里叶变换、小波变换、S变换、改进S变换和Curvelet变换等。

1.1.3 其它方法

WANG等[9]提出了基于贝叶斯反演的地层衰减补偿方法,在反射系数序列稀疏的假设下,先构造衰减矩阵,然后利用贝叶斯理论以实际地震资料为先验信息求解反演问题,实现了对非平稳地震记录的补偿,无须精确求取Q值,且能够较好地压制随机噪声,具有良好的稳定性,但该方法需要从实际测井资料中获取反射系数的分布特征。BAAN[10]将反Q滤波与时变Wiener反褶积相结合进行衰减补偿,首先利用稳定的反Q滤波技术对地震记录的衰减能量进行补偿,同时进行相位校正,消除其非平稳性,然后利用Wiener反褶积来压缩地震子波,扩展频带宽度,提高地震记录的分辨率[11]。

衰减补偿方法在实际应用中有着一定的限制条件,且人为对非平稳地震记录进行高频衰减补偿很容易出现欠补偿或过补偿的情况,难以保证地震记录的真实性。因此,基于衰减补偿的时变子波提取方法目前难以提取出高精度的时变地震子波。

1.2 分段处理方法

在地震资料处理过程中,处理非平稳地震记录最简单常用的方法就是分段处理。分段提取时变子波的思想是将非平稳地震记录划分为若干段,每段地震记录视为近似平稳,再结合其它方法提取子波。分段处理方法在子波振幅与相位的提取中均有广泛应用。

显然,此类方法的关键是合理分段的有效实现,目前常用的分段方法有均匀分段、重叠分段、自适应分段等方法。MARGRAVE等[12]将地层视为均匀粘弹性介质,在反射系数序列白噪的假设条件下,采用矩形窗平滑均匀分段对地震记录作Gabor变换。BAAN[13]将非平稳地震记录分解成若干等长的重叠片段,在子波常相位的假设下,在每段内基于峰度最大值准则提取子波相位,再将提取的相位延拓至每一采样点,实现子波相位的提取和校正。高静怀等[14]结合地震记录的Robinson模型及Goupilaud模型,提出了一种地震记录的变子波模型,该模型的近似数学表达式为:

(1)

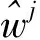
此外,基于分段处理的子波提取方法普遍存在以下两方面问题:一方面是分段数量的选取,若分段数太少,无法充分反映子波的时变特性;若分段数太多,则每段地震记录所含的数据量太少,无法精确提取出地震子波。另一方面是分段方法的应用,若分段的方法选取不当,提取出的子波可能会掩盖相邻地层间子波振幅和频率成分的变化。

1.3 应用于补偿或分段处理后地震记录的子波提取方法

非平稳地震记录经过衰减补偿或分段处理后,整体或分段内可看作近似平稳,然后采用自相关法、同态法、高阶统计量法和常相位旋转法等传统的基于时不变假设的子波提取方法实现子波的估计。

1.3.1 自相关法

自相关法假设反射系数为白噪声,则地震记录的自相关等于子波自相关,因此利用地震记录的自相关即可得到子波的振幅谱。但真实的反射系数序列基本无法满足白噪的假设,且二阶统计量不包含子波的相位信息,故自相关法仅能估计最小相位子波,方法的应用受到较大限制。

1.3.2 同态法

同态法根据子波的复赛谱(对数谱)分布在原点附近,而反射系数序列的复赛谱远离原点的特性,将子波与反射系数序列进行分离,达到提取地震子波的目的。刘春成等[16]通过调节改进广义S变换参数,获得衰减地震记录的时频谱,将其变换到复赛谱时频域提取子波振幅谱。

1.3.3 高阶统计量方法

假设反射系数序列是一个独立的、同分布的、非高斯的随机过程,则地震数据的高阶累积量与地震子波的高阶累积量仅相差一个比例系数,通过估算地震数据的高阶累积量即可实现地震子波的提取[17]。戴永寿等[18]先通过时变维纳滤波法将振幅谱的影响从地震记录中消除,将处理后仅残留相位部分的地震记录视为近似平稳,然后用高阶统计量的双谱法重构子波相位谱。

1.3.4 常相位旋转方法

常相位旋转方法假设子波相位是与频率无关的常数,利用希尔伯特变换对地震记录进行相位扫描和校正,当评价准则达到最大值时即估计得到子波相位。通常使用的评价准则有峰度最大值准则[13]与偏斜度最大值准则[19]。刘俊州等[20]通过数值模拟试验说明偏斜度准则函数在动态范围、稳定性、抗噪效果等多方面都要优于峰度准则函数,但当噪声为一定频率范围内有色噪声时,二者在相位表现方面都出现较大的偏差。WANG等[21]提出了一种基于Rényi散度的评价准则,相较于峰度最大值准则,在低频时相位估计更加准确。

现有的衰减补偿方法很容易出现欠补偿或过补偿的情况,难以保证地震记录的真实性;而分段处理方法又无法很好的体现地震记录的非平稳性,故目前基于高频补偿和分段处理的子波提取方法的实际应用效果仍有待改进。

2 基于振幅相位匹配融合的时变地震子波提取方法

分别估计子波振幅谱和相位谱再进行匹配融合能够在无须衰减补偿和分段处理的情况下直接从非平稳地震记录中提取具有时变特征的地震子波。接下来将分别总结子波振幅谱和相位谱提取方法的研究进展。

2.1 振幅谱提取方法

对非平稳地震记录进行时频变换后再应用谱模拟方法拟合振幅谱是目前提取时变子波振幅谱的有效方法,故本节将对现有的时频分析和谱模拟方法进行总结。

2.1.1 时频分析方法

地震信号属于非平稳信号,常规傅里叶变换方法仅能分析信号的频域特性,无法准确描述频率分布随时间的变化情况。而时频分析方法能够将一维时域信号变换到二维的时频平面,全面反映地震信号的时频联合特征[22],且无需任何假设条件地适用于非平稳信号[23],在非平稳地震记录处理的各个环节中发挥了重大作用。

经典的时频分析方法主要有短时傅里叶变换[24]、小波变换[25]、S变换[26]和广义S变换[27]等,这些方法通过构造各自的窗函数以截取信号,并在沿时间方向移动的时窗内对截取的信号作傅里叶变换对信号进行时频分析,窗函数的选择导致这些方法存在各自的局限性:短时傅里叶变换的窗函数固定,无法兼顾时间分辨率与频率分辨率;小波变换是一种时间-尺度分析方法,尺度因子与频率的关系不确定,导致应用范围受到一定限制;S变换窗函数以固定的趋势随频率变化,不能根据具体的应用而调整,缺乏灵活性;而广义S变换受测不准原理的制约,无法同时达到最佳的时间分辨率和频率分辨率。为了解决这些问题,国内外学者又不断研发了更多时频分析方法。HUANG等[28]提出了经验模态分解(EMD)方法,将一个具有复杂频率成分的多分量信号自适应地按照频率的高低分解为一系列分量之和,这些分量称为为本征模态函数(IMF),即:

(2)

式中:x(t)为目标信号;ci为第i个IMF分量;rn为剩余分量。而后,WU等[29]再次提出了一种更为稳定的集成经验模态分解(EEMD)方法,该方法通过多次向信号中添加固定百分比的高斯白噪声,再对经过EMD处理后的数据进行多次平均处理,在一定程度上解决了模态混叠效应,但是仍存在不能保证完全重构信号以及分解出的IMF不唯一等缺点。YEH等[30]通过在EMD分解信号过程中的每一阶段添加特定的白噪声,同时计算一个唯一残差来获得每个符合定义的IMF,将EMD发展为互补集合经验模态分解(CEEMD),解决了EMD中的模态混叠问题,并实现了原始信号精确重构。DAUBECHIES等[31]提出了应用于时频域信号的同步压缩变换,该方法通过提取时频谱的瞬时频率信息,对时频平面的能量在频率方向进行重新分配,极大地提高了频率方向的清晰度。WANG等[32]开发了广义β小波族(GBWs)作为连续小波变换的母小波,通过改变控制小波形状的两个参数(α和β),实现自适应地权衡时间分辨率与频率分辨率。姚振岸等[33]首先对非平稳地震道作基追踪谱分解,将地震信号分解到预先定义的波形字典的各个基函数上,然后求得基函数表示系数,经尺度到频率的映射,得到高分辨率谱分解结果,再逐个时间点提取地震子波,该方法能够同时获得较高的时间和频率分辨率。时频分析方法将时间域的信号映射到时频域,在二维时频谱中进行相关处理,能够较为准确地同时定位时间和频率信息,是时变子波提取的有力工具。

2.1.2 谱模拟方法

谱模拟方法的主要思想是对地震子波振幅谱进行参数化建模,从地震记录的振幅谱中拟合出子波的振幅谱[34]。该方法最早由ROSA等[35]提出,假设子波振幅谱是类似于雷克子波的光滑单峰曲线,在频率域建立数学模型:

(3)

式中:k为常数;N为阶数;an为关于f的多项式的系数。一般地,0

尚新民等[1]采用改进S变换对地震记录进行时频分析,然后利用(3)式对不同时刻地震记录的振幅谱进行最小二乘拟合实现时变子波振幅谱的提取。谱模拟方法能够突破反射系数序列白噪的假设,原理简单、效果明显,在子波振幅谱的提取中得到广泛应用。李振春等[36]通过改变谱模拟参数拟合出一簇地震子波振幅谱,然后计算各拟合子波的自相关与从地震记录中估算出的子波自相关之间的误差,误差最小时即确定为最优的子波振幅谱,提高了谱模拟方法的适应性和准确性。MAMASANI等[37]通过可分非线性最小二乘算法找出多个不同峰值频率的最优Ricker子波以重建子波振幅谱,避免了多项式谱模拟中参数的选择,求解效率较高。唐博文等[38]建立了二次谱模拟方法的基本原理,假设地震子波的振幅谱是光滑的,且与反射系数的二次谱可分,则可设计一个低通滤波器作用于地震记录的二次谱,滤除高频成分,重构低频成分,实现子波振幅谱的估计。

目前谱模拟方法是子波振幅谱提取最常用的方法,但此类方法要求子波振幅谱满足类似于雷克子波的单峰、光滑的曲线的假设,限制了子波振幅谱的形态,且多项式中的参数N难以选择;基于优势Ricker分量的谱模拟方法在子波振幅谱形态不满足假设条件时,估计误差较大;二次谱模拟方法构造的低通滤波器的截止频率等参数只能依靠人工设定。

2.2 相位谱提取方法

为了解决分段方法受限于子波分段平稳假设的问题,局部相似度和纯相位滤波器寻优等方法常被应用于子波相位估计中。

2.2.1 局部相似度方法

局部相似度方法的主要思想是先将地震道进行相位旋转,计算旋转后的地震道与标准道的相似度,相似度达到最大时的旋转相位即为最优相位。BAAN等[39]和FOMEL等[40]提出将相位估计看成最小二乘反演问题,将地震道的包络看作标准道,不断改变地震数据的相位,利用相位与地震记录包络的局部相似度作为判别准则来估计子波相位。DAI等[41]对这一类方法做了进一步的改进,首先利用高阶累积量的双谱估计相位范围,然后在预估范围内进行常相位旋转,并利用局部相似性优化法准确提取时变子波相位谱,解决了单独使用双谱估计相位不准确以及局部相似性优化方法计算量过大的问题。该方法以常相位旋转法为基础,须假设子波为常相位或不同时刻子波相位的变化量为常数,存在一定的局限性。

2.2.2 纯相位滤波器寻优方法

纯相位滤波器寻优方法的思想是在子波振幅谱已知的条件下,通过改变子波Z变换零极点的分布情况,构造由一系列相同振幅谱不同相位谱组成的子波库,再通过优化算法从中选择使得准则函数达到极值的子波。张亚南等[42]采用单位化自回归滑动平均(ARMA)模型振幅谱来构造纯相位滤波器,并在最大方差模准则约束下,采用改进的粒子群算法对子波相位残余进行非线性寻优。WANG等[43]提出了基于蚁群算法的子波相位估计方法,首先对子波振幅谱进行希尔伯特变换估计最小相位子波,然后将最小相位子波Z域的零点关于单位圆进行对称变换,建立候选子波库,最后利用蚁群算法实现子波相位的准确寻优。该方法在有色噪声的影响下具有较好的稳定性,但蚁群、粒子群算法等在确定寻优初值方面还有待进一步研究。

2.2.3 其它相位估计方法

VOSOUGHI等[44]将混合相位子波视为最小相位子波与全通子波的褶积,首先从地震记录中求出最小相位子波,再使用累积量匹配法从谱白化后的地震数据中得到全通子波,最后将二者褶积得到混合相位子波。此方法能够增加数据带宽,且算法简单、计算速度快,但对数据带宽与中心频率之比有严格要求。ZHANG等[45]根据粘弹性介质中地震波的传播规律,以地层品质因子Q为中间桥梁,推导建立了子波振幅谱和相位谱的关系,从而利用所估计的子波振幅谱准确估计时变子波相位谱。

目前基于振幅相位匹配融合的时变地震子波提取方法通常存在限制子波振幅谱形态,子波相位局限于分段平稳或常相位假设的问题,但此类方法相较于基于衰减补偿的子波提取方法,提取的子波更为准确,是今后研究的重点方向之一。

3 总结与展望

本文分析了主流时变子波提取方法的研究进展,详细总结了现有方法的优缺点及适用条件,从而得出结论:高频衰减补偿与分段处理方法严重依赖于地层衰减的估计精度,分段数目与分段方法的选择等因素,因而应用范围受限。谱模拟等时变子波振幅谱提取方法限制了子波振幅谱的形态,当子波振幅不满足假设条件时,提取效果不佳。现有时变子波相位谱提取方法大多局限于子波常相位或分段平稳假设,难以应用于复杂地层衰减、强噪声干扰的地区。如何改进现有方法从而有效提高子波估计精度是目前亟待解决的问题。同时,随着地震勘探技术的不断发展,研究目标已经逐渐转向深层复杂构造的准确成像,对地震子波提取以及高分辨率地震资料处理的方法研究也提出了更高的要求。

综上所述,目前时变子波提取方法的实现普遍建立在地下介质线性衰减、噪声高斯分布等假设条件下,但实际情况往往更加复杂,非线性衰减与非高斯噪声干扰等会对地震子波的准确提取产生严重的影响。同时,因深层相对于中浅层具有信噪比更低、传播路径更复杂、衰减更严重等特点,现有子波提取方法难以直接应用于深层地震资料处理。此外,深层复杂构造的研究对勘探精度有着更高的要求,利用叠后地震数据提取出的子波无法完全满足全波形反演和偏移成像等处理环节的实际需求,而利用包含更多信息的叠前地震数据提取子波能够更可靠地揭示地下储层的分布情况。因此今后的研究工作将主要从以下4方面展开。

1) 将现有时变子波提取方法扩展应用至非线性衰减、非高斯噪声干扰条件下,研究品质因子Q随频率变化时的子波提取方法。

2) 进一步关注智能信息处理技术的前沿发展,研究适用范围更广的时变地震子波提取方法。

3) 针对部分地区深层油气勘探面临的信号弱、分辨能力不足等问题,开展强衰减、低信噪比条件下的子波提取方法研究,并利用提取的子波对地震数据进行高低频补偿,拓宽频带,提高地震资料的分辨率。

4) 开展叠前地震数据中子波提取方法的研究,并应用于全波形反演和叠前偏移,有效提高速度建模与成像精度。