Magnus效应下的前缘旋转圆柱参数设计

曹 阳 ，戚嘉伟 ，吴国庆 ，李锦义

（1.南通大学机械工程学院，江苏 南通 226019；2.江苏省风能应用技术工程中心，江苏 南通 226019）

1 引言

目前，风力机叶片翼型大多是从传统的航空翼型演化而来[1]，而风力机叶片的运行环境具有风速低，风速风向多变等特点。传统叶片在很大程度上难以跟上风力机的快速发展[2]，因此根据风电机组研发需求，大力发展叶片技术，提高自身创新能力，研究新型叶片结构成为了风电技术发展的重要方向之一。

Magnus效应（Magnus Effect）主要是指在流场中旋转的圆柱或者圆球受到侧向力的一种流体力学现象。这一物理现象是于1852年柏林物理学家Magnus所提出[3]。这一个世纪以来，对旋转圆柱绕流和Magnus效应有了很大的进展。在上世纪九十年代，Modi课题组[4]提出通过运动表面来控制边界层分离的想法。他们在翼型的前缘，尾缘或者翼型上表面处添加可旋转圆柱，结果表明了该方法能有效地推迟失速，提高升力系数。

本研究在NACA0015翼型前缘添加可旋转圆柱，利用前缘高速旋转圆柱抑制翼型吸力面的流动分离并推迟失速[5]，即Magnus效应的延伸与应用，从而提高翼型的气动性能。分析了圆柱与主体间间隙大小及圆心距离前缘位置两个几何参数与翼型升阻比的关系，确定了一组具有最佳气动特性的旋转圆柱参数。利用确定的新翼型建立2D垂直轴风力机模型，通过数值模拟分析Magnus效应下的垂直轴风力机的功率、风能利用系数，并通过实验验证其合理性。

2 前缘旋转NACA0015翼型的计算模型与条件设置

均采用ICEM前处理软件进行计算区域的建立与网格划分。二维前缘旋转NACA0015翼型的计算网格，如图1所示。计算区域的外流场边界延伸至翼型弦长的15倍。计算域网格分为两部分：第一部分为总体C型网格，一周的网格点数为413，径向网格点数为89；第二部分为旋转圆柱周围的环形区域O型网格，一周的网格点数为160，间隙处网格点数为80。为满足y+计算要求，物体表面第一层网格设置为弦长的10-3倍。两部分合并即可得到最终网格。

图1 二维前缘旋转NACA0015翼型的计算网格Fig.1 Grid for a Two Dimensional NACA0015 Airfoil of Rotating Leading Edge

此处计算采用RNG湍流模型，选用基于压力隐式SIMPLE算法求解，采用二阶迎风差分离散格式。进口为速度入口边界（Velocity Inlet）；出口为压力出口边界（Pressure Outlet）；旋转圆柱表面为运动无滑移壁面边界（Wall）；翼型表面为无滑移固壁（Wall），两部分网格交界处的边界类型为Interface。

3 前缘旋转NACA0015翼型的形状设计

翼型间隙大小是指旋转圆柱与翼型主体之间的距离。圆心位置是指旋转圆柱的圆心位于弦长上距离前缘的位置。弦长，间隙，圆心位置分别用L，c，o表示。此处翼型弦长L=1000mm，间隙大小分别为c1=1.2mm，c2=2.2mm，c3=3.2mm，圆心位置分别是10%L，15%L，20%L，25%L 处。图 2（a）为四种不同圆心位置的前缘旋转NACA0015翼型示意图，图2（b）为三种不同间隙的前缘旋转NACA0015翼型示意图。

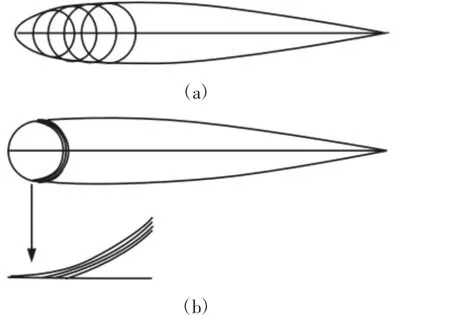
图2 四种不同圆心位置及圆心位置在25%弦长处不同间隙示意图Fig.2 Sketch Map of Four Different Center Location and Center Position of the 25%Chord of Different Gap

4 不同间隙和圆心位置的计算分析

雷诺数越高，雷诺数变化所引起的升力系数和阻力系数的变化越小，此处计算状态选取的为雷诺数Re=6.56×105，转速比（圆柱表面速度和来流速度之比）为4[6]。为不同攻角下翼型的升力系数变化，如图3（a）所示。由图3（a）可知，在小攻角下，各系列前缘旋转翼型的升力系数比较接近，但施加前缘旋转圆柱的翼型升力系数明显比控制前的NACA0015翼型要高，随着攻角的增大，升力系数也随之增大，攻角8°时，传统翼型的升力系数与控制后的翼型差不多，攻角16°后，传统翼型升力系数开始下降，而大部分控制后翼型的升力系数仍在增大。

图3不同攻角下翼型的升力系数、阻力系数、升阻比变化Fig.3 Lift Coefficien t＆ Drag Coefficient＆ Lift-drag Ratio of Airfoil at Different Angles of Attack

图3 （b）为不同翼型阻力系数随攻角的变化，如图所示前缘旋转翼型阻力系数随攻角的变化趋势基本一致，均为先减小后增大。在攻角为（0～4）°时，传统翼型阻力系数略小，比控制后的翼型存在优势，但是随着攻角的增大，传统翼型阻力系数也随之增大，而控制后的翼型在（4～12）°仍处于减小状态，之后开始增加，但仍小于传统翼型阻力系数。翼型的升阻比随攻角的变化，如图3（c）所示。从图中可看出，升阻比曲线图可分为三个等级，下方部分是间隙为c1系列的翼型，中间部分是间隙为c2系列的翼型，上方部分是c3系列翼型，综合来看，显然间隙c3系列翼型存在优势。c3_0.15翼型与c3_0.25比较而言，虽然低攻角时c3_0.15升阻比较大，但整体而言，c3_0.25的优势体现在大攻角的时候，也就是说，c3_0.25增大有效攻角，延迟失速。故c3_0.25具有较好的气动性能。因c3_0.25是这一系列参数数据中的边缘处，为验证所得结论的正确性与严谨性，将其分别与c3_0.30和c4_0.25进行比较。是c3_0.25与c3_0.30即间隙仍是3.2mm，如图4所示。圆心位置在30%弦长处的翼型的升阻比变化图，由图4可知c3_0.25系列翼型具有明显的优势。图5是攻角为10°间隙为c4即间隙是4.2mm，圆心位置在25%弦长处时候速度云图，以图5为例，前缘高速旋转的圆柱带动了吸力面气流向后推移，提高了气流动能，抑制翼型尾端的气流分离，这便是前缘旋转圆柱在Magnus效应下对翼型气动性能的提升作用。但c4_0.25因间隙过大，圆柱旋转在间隙处形成的气流一部分从间隙下方流走，吸附在翼型下表面，使得翼型上下表面速度差减小，致使压力差变小，对抑制翼型尾端的流动分离明显弱于c3_0.25系列翼型。

图4 不同攻角下c3_0.25与c3_0.30升阻比变化Fig.4 Lift-drag Ratio of c3_0.25 Airfoil and c3_0.30 Airfoil at Different Angles of Attack

图5 c4_0.25速度云图Fig.5 Velocity Contour of Velocity Contour

因此综上分析可得出，当控制前翼型弦长为1000mm时，前缘旋转圆柱间隙为3.2mm，圆心位于距前缘25%弦长位置处的翼型具有较好的气动性能。

5 Magnus效应下的垂直轴风力机模型

将已获得具有较优气动性能的前缘旋转NACA0015翼型为基础建立二维垂直轴风力机模型。此处控制前传统翼型弦长为140mm，则旋转圆柱间隙变为0.448mm，圆心位置仍为25%弦长处，控制后的翼型弦长为115.836mm。风力机基本参数为：叶片数3，叶轮半径500mm，叶轮叶片安装角5°。

5.1 计算区域与网格划分

为简化计算，模型构建时暂不考虑转轴部分[7]，同时更能突出新翼型的改造性能。并且这里划分网格的对象为流体，因此，需将构建好的模型去除固体叶片和固体圆柱，则剩下部分为流体计算域以坐标原点为旋转轴的旋转中心，整个外流场的四个顶点坐标（单位为 mm）分别为（-6000，6000），（-6000，6000），（18000，6000），（18000，-6000）。Z1区域和Z3区域均为静止区域，Z2区域即翼型所在的环形区域为旋转区域，风轮半径R为500mm，令内圆半径R1和外圆半径R2分别是叶轮半径的0.8倍和1.2倍，则分二者半径别为400mm和600mm。

Magnus效应下的垂直轴风力机整体计算区域网格划分，如图6所示。计算域网格分为六部分，且六部分均采用结构网格划分，网格总数为121707。第一部分为Z1静态圆形区域，采用O型网格划分，网格总数为20275。第二部分为Z2滑动区域，这部分也是重点划分区域，首先进行块划分然后再生成网格，经过块划分后生成的网格具有很好的正交性，均是四边形网格，并在翼型处采用了O型网格，为了保证计算精度，已在翼型表面区域做了加密处理，网格数为70236。第三部分为Z3静态区域，即外部的外流场区域，也进行了块划分，并生成了如图6（a）所示正交性很好的四边形网格，网格数为26024。剩下的三部分即为三个旋转圆柱周围的环形区域，均采用O型网格划分，网格数均为1724。

图6 网格划分Fig.6 Grid Partition

5.2 边界参数设定

（1）入口边界即外流场左边线选取速度入口边界（VelocityInlet），速度大小为 10m/s，方向水平向右[8]；

（2）出口边界即外流场右边线选取压力出口边界（Pressure Outlet），给定相对压力为 0Pa；

（3）外流场上边线、下边线为无滑移、无渗透壁面（Wall）；

（4）旋转圆柱表面和翼型表面为运动表面无滑移壁面边界（Wall）；

（5）翼型所在旋转环形区域的内圆边线和外圆边线，三个圆柱周围间隙与旋转环形区域交界处为滑移边界（Interface），以便内外网格传输数据。

5.3 计算方法

数值模拟中，采用了S-A（Spalart-Allmaras）湍流模型，它是非常有效的低雷诺数湍流模型，不仅能处理复杂的流动，且对内存和CPU的要求低。选用基于压力隐式SIMPLE算法，二阶迎风差分离散格式[9]。运用滑移网格技术对垂直轴风力机二维流场进行瞬态求解。瞬态计算和时间相关，在Fluent中需设定计算步数和单步计算时间。考虑到实际情况，设叶轮每一时间步转动2°，单步内计算迭代60次[10]。

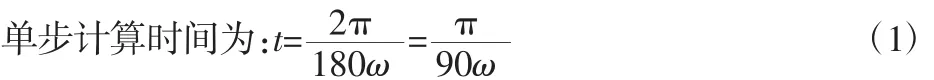
式中：ω—叶轮旋转角速度，单位为rad/s。

6 数值模拟结果分析

风力机叶片产生的转矩M是作用于风力机叶片的空气动力与力臂的乘积。在Fluent中仿真能得到三个叶片的转矩。通过检测每个叶片的转矩系数Cm，则可由下面的公式计算得到：

式中：M—转矩（kg·m）；ρ—空气密度（kg/m3）；R—叶轮半径（m）；S—叶轮的扫风面积（m2）；V—上游风速（m/s）；Cm—扭矩系数。

在 Fluent仿真中，因参考值设置，0.5ρRSV2=0.6125，则 M=0.612Cm，所以转矩系数乘以0.6125即为风力机的转矩。

转矩随时间呈周期性变化，负值为推动风力机转动的转矩，正值为阻止风力机转动的转矩。虽然风力机在整个旋转过程中，它的总转矩是呈正负周期性变化，但是在旋转一圈的过程中，推动风力机转动的转矩所做的功始终是大于阻止风力机转动的转矩所做的功，这符合实际情况。由以下公式则可得到功率和风能利用率。

式中：P—风力机实际获得的功率（W）；M—转矩（kg·m）；ω—角速度（rad/s）；E—气流动能；ρ—空气密度（kg/m3）；S—叶轮的扫风面积（m2）；V—上游风速（m/s）。

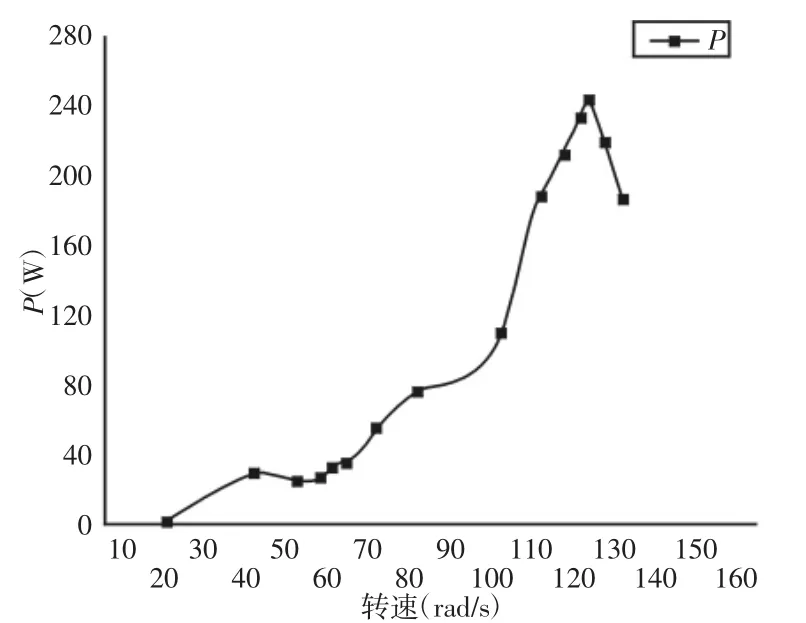
图7 叶轮功率随转速的变化Fig.7 Power with the Rotating Speed

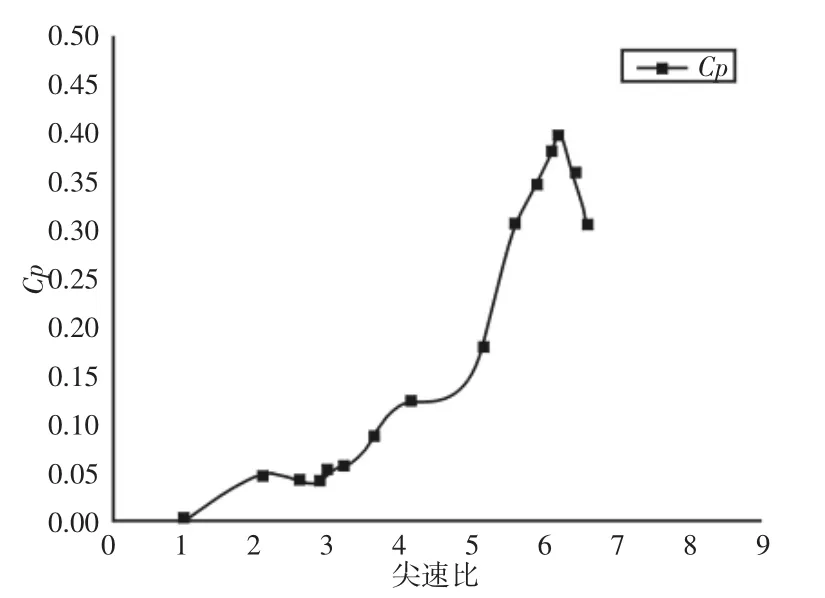
图8 风能利用率随尖速比的变化Fig.8 Cp with Tip Speed Ratio

不同转速下功率的变化曲线，如图7所示。不同尖速比下风能利用率的变化曲线，如图8所示。从这两张图中可以看出，风能利用系数随尖速比的变化与叶轮功率随转速的变化基本一致，整体上呈现先增大后减小趋势。在低尖速比时，风能利用率增加较慢，随着尖速比的增大，在实际工况下，依据叶片设计手册，三叶片非扭转翼型小型风力发电机尖速比多在4～6。当叶尖速比超过6后，实际叶片无法达到，并无实际研究意义。因此，在λ=6附近处，风能利用率达到0.334，可认为是理论最大值。同样，在转速120rad/s附近处，功率达到理论最大值为210W。

7 模型试验

安装完好的风机试验模型，如图9（a）所示。主要零部件包括立柱、发电机、齿轮副、旋转风轮。旋转风轮由旋转套筒、叶片支撑杆、叶片组成。叶片前缘处安装旋转圆柱，由两端滚动轴承支承并由直流电机驱动旋转，如图9（b）所示。实验阶段使用直流稳压电源提供动力，直流电源与旋转风轮通过电刷进行运动转换。为接近自然风特性，试验采用鼓风机产生实验风，轴流鼓风机产生的风带有自然风的不确定性，能更好模拟风机在自然环境中所产生的特性和输出功率。实验过程中先启动电动机，让前缘旋转圆柱转动，再启动鼓风机，在风轮运转情况下，前缘高速旋转圆柱。通过前缘旋转圆柱自身的旋转与风轮在鼓风机所形成流场中旋转，激发Magnus效应，提升新翼型的气动性能。

图9 风机整体试验模型Fig.9 Experiment Model of Wind Turbine

在本试验过程中通过测量风轮的转速，观察同样风速下圆柱不旋转与旋转对风轮性能的影响。同时通过测量发电机输出电压观测风力机连续运转性能，发电机输出电压与风轮转速成线性关系。在不同风速下测得圆柱不旋转与旋转时对风机性能的影响，结果如图10所示。圆柱不旋转的情况近似于传统叶片的风机性能，圆柱旋转的转速为1500r/min。从图上可见在不同风速下旋转圆柱对于风轮转速有不同程度的提升，计算得平均提升率为7.4%。

图10 圆柱不旋转与旋转对性能的影响Fig.10 Performance with Cylinder Not Rotating and Rotating

8 结论与展望

研究了一种利用Magnus效应，在前缘附加旋转圆柱的NACA0015翼型的气动性能，通过数值仿真与实验相结合，主要取得了如下成果：（1）数值仿真与计算分析结果表明，当控制前翼型弦长为1000mm时，前缘旋转圆柱间隙为3.2mm，圆心位于距前缘25%弦长处的翼型具有较好的气动性能，且该新型垂直轴风力机风能利用率能达到0.334；（2）搭建实验平台，测试风机模型的性能，验证了旋转圆柱对风机的提升作用，平均提升7.4%；（3）综合数值仿真与模型试验的结果可看出，将Magnus效应应用到叶片空气动力性能改善中，使前缘旋转圆柱抑制翼型表面的流动分离并推迟失速，能使垂直轴风力机功率输出有一定程度的提高。该研究仅对数值仿真计算结果进行了必要的分析，搭建了简单的实验平台，下一步还需进行的工作有：（1）进行多来流风速及叶片转速下的升阻比计算，作为衡量所设计翼型气动性能优劣的依据；（2）在已有二维模型基础上，将转轴纳入考虑进行全三维计算；（3）重建模型，减少旋转圆柱与叶片机体间隙，以获得更全面的实验数据。