基于相似性分析的主动再制造优化设计方法
2020-03-28柯庆镝刘光复宋守许
吕 岩,柯庆镝,刘光复,宋守许
(合肥工业大学机械工程学院,安徽 合肥 230009)
1 引言
再制造是通过先进技术手段,使不再具备功能的废弃产品恢复到不低于原有性能规格的过程。由于再制造能够有效降低产品在整个生命周期里的成本和环境负担,日益受到企业及社会的重视。目前再制造毛坯主要来自于废旧产品,由于废旧产品的服役时间和载荷环境存在差异性,导致再制造毛坯数量和质量参差不齐,大大增加了控制再制造过程的难度,进一步阻碍再制造工程的工业化进程。针对再制造过程离散程度大、成本高的问题,一些学者提出了主动再制造的概念,如文献[1]建立了基于冗余强度的主动再制造时机抉择数学模型,并提出了主动再制造时域抉择方法;文献[2]从产品角度入手,阐述主动再制造设计理论,建立现代产品的设计方法框架;文献[3]提出了基于性能参数的主动再制造时机抉择评价模型;文献[4]提出面向主动再制造的可持续设计理论,研究了产品模块化设计,并在此基础上探讨了基于神经网络的主动再制造时机抉择方法。以上研究均对主动再制造相关理论及方法进行了分析与研究,但大部分都是理论框架的搭建与定性研究,缺乏具体的数学模型与公式,无法为主动再制造的设计参数优化提供依据,以及为设计方向提供指导。
另一方面,产品在生命周期过程中所体现出的性能,很大程度(70%)取决于设计阶段。因此,从设计阶段入手,分析并解决再制造中出现的各类问题是非常必要的。许多学者在再制造设计领域均开展了卓有成效的研究工作:文献[5]研究了再制造产品设计、增材制造等;文献[6]提出了一种基于模糊集理论和质量功能展开法的再制造设计方法;文献[7]提出了一种支持产品生命周期的再制造设计方法。以上这些再制造设计研究主要是将再制造阶段需求作为设计目标对产品设计方案进行优化设计,但还缺乏针对主动再制造设计的需求分析,缺少基于设计参数映射模型的再制造设计方法,无法反映产品设计参数改变时其性能的变化趋势,不能有效降低再制造过程的不确定性。
因此,结合主动再制造时域决策分析,提取出产品的主动再制造设计需求,基于结构相似性分析方法,建立了性能相似性分析模型。并构建主动再制造设计中的优化参数及目标函数,提出了基于相似性分析的主动再制造设计方法。
2 主动再制造设计
传统的再制造工程,大多数情况下只在产品报废后被动地考虑零部件失效状态对其进行再制造修复,由于废旧零部件失效状态存在较大的不确定性,严重阻碍了再制造产业化进程。针对这一问题,相关学者提出了主动再制造,即综合分析产品全生命周期下的性能变化趋势得出最优决策,是在其经济性、环境性最佳时进行的再制造。通过选择在一个合适的时间区域内实施再制造,可最大程度上控制再制造毛坯数量和质量的离散性,实现产品在整个服役周期内的总体服役价值最优。
在服役过程中,产品的性能随着时间增加而逐渐减小,它们之间的映射关系即产品性能退化曲线,如图1所示。该曲线上有一小段对应再制造的最佳时间段,在此区域之前,产品再制造可能会产生大量浪费,在此区域之后,在当前技术条件下,产品丧失再制造价值,这一时域称为主动再制造时域(TPR),即当产品性能减退至接近拐点时,主动对服役产品实施再制造的最佳时间区域。此时进行再制造不仅能使产品恢复甚至超越原有的性能水平,还可以实现再制造产品最佳的碳排放、经济性以及可再制造性。
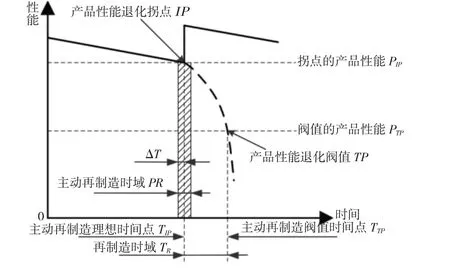
图1 再制造中的产品性能曲线Fig.1 Product Performance Curve in Remanufacturing
因此,主动再制造时域分析是主动再制造的关键问题,应当重点量化分析主动再制造时域对产品结构设计的约束与要求。在服役期间,产品内部的关键零部件失效状态不断演化,一方面对产品性能的变化起着决定性作用,另一方面也影响着产品再制造阶段的可行性分析。要使产品在整个服役周期内性能最佳,必须首先分析主动再制造时域对产品关键件的设计要求,优化关键件的再制造时域使其达到最佳时域,从而达到主动再制造时域对产品设计的要求。可表示为:
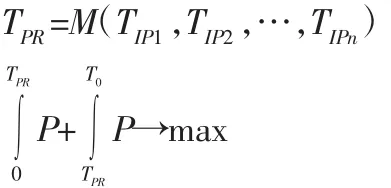

图2 产品的性能退化Fig.2 Product Performance Degradation
对于产品里的关键件而言,为了满足主动再制造时域的要求,需要进一步研究设计参数、载荷条件和性能之间的映射关系,使关键件的设计参数满足在一定载荷条件下性能要求,即调控其性能演化过程,使其满足主动再制造时域相关需求。可表示为:

再通过对传统公式的演化推导,建立关键件结构设计参数与其性能之间的数学映射关系,提出主动再制造设计目标函数:
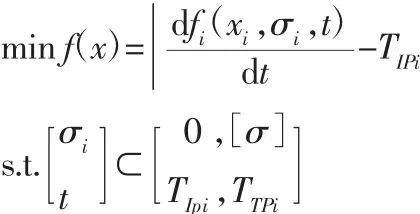
式中:Pi—关键零部件i的性能;fi—性能与其他参数的映射关系;xi—结构的第i个设计参数;σi—所受应力;t—服役时间;TTPi—性能退化阈值点;TIPi—主动再制造理想时间点。
综上可知,对产品的主动再制造设计应从关键零部件入手,将主动再制造时域需求转化为对零部件性能演化的设计需求,对相关功能结构进行优化设计。
3 相似性分析
3.1 结构相似性
结构相似度是指产品结构件上承担某一特定功能或负载的通用性结构,如轴颈结构、键槽结构、花键结构等的相似程度的度量。由于相似性可以描述结构演化的过程,一些学者应用相似性理论进行了设计方法的研究,如文献[8]提出了构建具有与大变速箱相同负载能力的小尺寸相似模型的理论方法并进行验证;文献[9]应用几何相似性和拓扑相似性提出了基于特征的模型相似性测量的分层方案;文献[10]研究了系统或部件间的相似性,将已有的系统或部件的设计应用于新的设计之中;文献[11]研究了机械系统的相似分析原理,进行相似元数值和系统相似度的计算,提出了相似系统度量的基本方法。基于以上研究中可以得到,分析机械结构几何设计参数之间的相似程度,就能够量化机械结构之间的结构相似性。两个相似结构A与B之间的形状相似函数可表示为:

3.2 性能分析
机械产品在一定的载荷作用下,不同几何结构会产生不同程度、不同形式的失效,而关键零部件的失效是产品性能下降的主要原因,即产品性能取决于关键件的失效情况。基于退役零部件失效统计数据,针对常见失效形式进行分析。
磨损失效(Wear):磨损量的理论计算通常采用Archard方程,其结构表面的磨损深度可表示为:

式中:h—线磨损深度/mm;Kd—线性磨损系数,单位为mm2/N;滓—接触点处的接触应力/MPa;l—滑动距离/mm。
由上式可知,零部件结构表面的磨损深度与接触应力和滑动距离成正比,其中接触应力取决于残余应力、热应力、润滑、接触面的几何形状等因素。
疲劳失效(Fatigue):基于传统疲劳寿命预测Manson-Coffin公式,可得出应变与疲劳寿命之间的关系:

式中:Δ着—(真实)局部应变;N—理论疲劳寿命(应力循环次数);—疲劳强度系数;b—疲劳强度指数—疲劳塑性系数;c—疲劳塑性指数。
由上式可知,在材料本身的疲劳强度及塑性系数为常量的情况下,零部件结构的疲劳程度与局部应变有关,而局部应变又取决于结构负载、以及结构几何形状等因素。
3.3 相似结构的性能
基于零部件失效状态的关键影响因素分析,可以得到结构失效主要取决于该结构的几何参数以及其所受到的负载状态。因此,当外界条件使得两个具有相似结构的关键零部件失效情况有一定联系时,那么它们的性能之间也一定存在着联系。
在磨损失效作用下,两个相似结构的性能主要由其磨损量决定,即性能反比于磨损深度Pw∝h,由式(2)有:

当相似结构材料相同时Kd1=Kd2,在它们受不同接触应力、滑动不同距离发生磨损失效时,根据式(4)可推导出:

式中:PW1、PW2—它们的性能,接触应力滓、滑动距离l与结构几何形状和所受负载有关。
对于疲劳失效,由式(3)可推导出:

对于多数金属材料,疲劳强度指数b变化范围为(-0.06,-0.14),疲劳塑性指数c变化范围为(-0.5,-0.7),疲劳塑性系数;对于典型的机械零件而言,N>105。因此有:

则式(6)可近似转换为:

在疲劳失效作用下,结构的性能主要由其疲劳寿命决定,即性能正比于疲劳寿命:PF∝N。又由于真实局部应变正比于名义应力:Δ着∝Δ滓。根据式(8),当两个相似结构受到不同的载荷,产生不同真实局部应变时有:

式中名义应力正比于加载应力:Δ滓∝滓,根据应力的定义滓=F/A,它与力F和受力面积A有关,而A与设计参数x有关;结构的疲劳强度系数、指数b与它的尺寸、载荷、材料、工艺等因素有关,但是对于相似结构,材料、工艺等因素的影响可以忽略。
引入形状相似函数SS(x1x2)=x1/x2,综上所述,对于零部件的常见失效形式,其性能只与应力和设计参数有关,因此相似结构的性能之比可统一表示为:

以发动机连杆为例,考虑其主要参数大小头直径和D、d中心距 l,即 x={D,d,l}。参照结构相似度公式(1)并结合式(10),设连杆的性能相似公式可表达为:

4 基于性能相似模型的主动再制造优化设计
根据企业调研及产品服役数据,对产品的再制造时域进行提取与分析,再进一步分析产品关键零部件的再制造时域、相关结构设计参数以及性能设计需求。而后结合性能相似分析模型,对相关设计参数进行反馈优化,分析其性能变化,实现对关键件再制造时域的主动调控,从而满足产品的主动再制造时域需求。
整个优化设计过程可分为量化性能需求、提取结构设计参数、分析相似结构和提出优化方案等四步。
(1)量化性能需求。该环节主要是将产品的主动再制造时域需求转化为性能的设计需求,以此为结构设计参数的优化提供方向。基于前期所确定的产品主动再制造时域,结合产品中关键零部件耦合关系,分析关键零部件的再制造时域,进而确定零部件性能优化目标函数:

(2)提取结构设计参数。该环节是在第一环节分析产品主动再制造性能需求的基础上进行的,主要是依据相关设计手册与企业数据,提取对零件性能影响程度较高的设计参数;基于产品的再制造时域需求,确定所提取设计参数的取值范围。进一步构建约束条件如下:

(3)分析相似结构。基于所提取的设计参数,分析待优化零部件Pi与优化目标零件Pj的性能相似性。基于形状相似性SS(xixj)=xi/xj,构建相似结构的性能相似函数为:

(4)提出优化方案。根据以上分析结果,联立方程组,则基于性能相似模型的主动再制造设计可表达为:

式中:0<σi,σj<[σ],TIP≤t≤TTP。
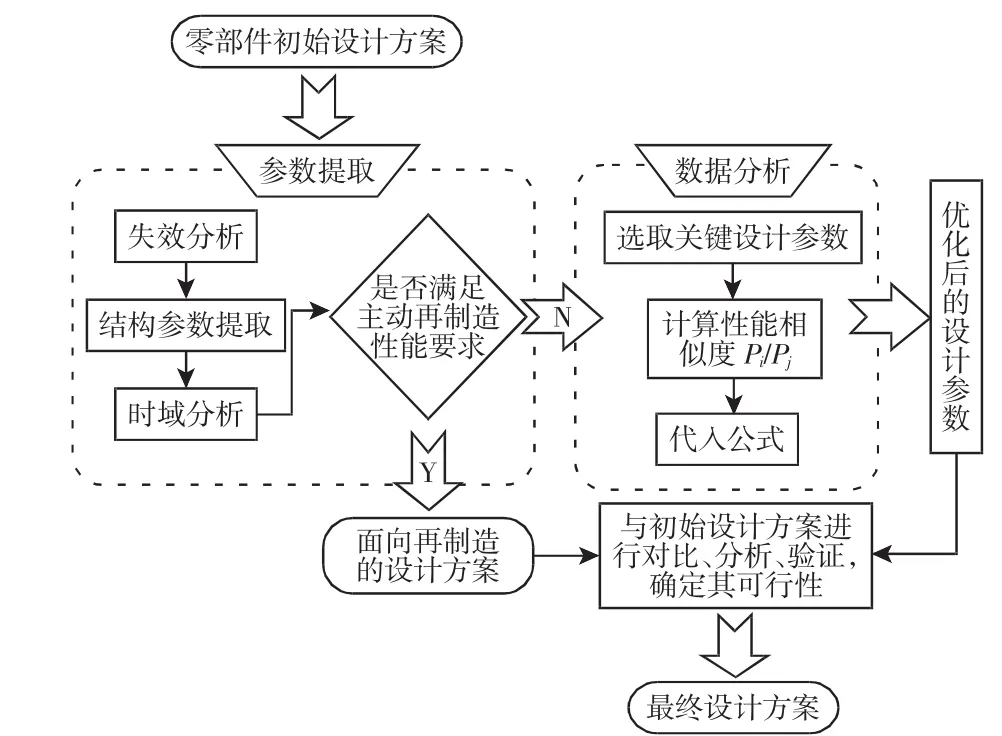
图3 基于性能相似模型的主动再制造优化设计Fig.3 Predecisional Remanufacturing Optimization Design Based on Performance Similarity Model
基于零部件的性能相似性分析结果,判断设计参数的优化方向。通过改变零部件的设计参数转换其性能,直到零部件的性能满足主动再制造设计要求或达到其参数优化极限。
5 案例分析
5.1 对比实验
发动机是再制造工程中的重要研究对象,而连杆作为发动机的关键件之一,其结构相对简单且变化多样。为了实现主动再制造设计的要求,连杆的性能需要与其他关键件的性能相匹配。发动机在进行一次拆卸时,可同时对连杆及其他关键件进行再制造,即它们的主动再制造时域接近或存在倍数关系。
以某型号发动机为例,选取连杆为研究对象,基于企业调研以及项目组前期工作数据,该发动机曲轴的主动再制造时间点为26.10万公里,活塞缸套的更换时间点为13.05万公里。根据再制造时域匹配的原则,初步设定连杆的主动再制造时间点为52.20 万公里。
利用仿真分析软件,建立发动机连杆的结构分析模型,加载求解,如图4所示。影响连杆寿命的因素有很多,为了方便研究,在保持连杆的厚度尺寸、材料属性等其他因素不变的情况下,得到最大压缩工况条件下不同大头直径D、小头直径d、中心距l和载荷F时的局部应力,再通过FE-SAFE软件计算相应条件下的应力循环次数,并求出修正系数,从而得出不同设计参数、不同载荷下的发动机连杆性能相似公式。
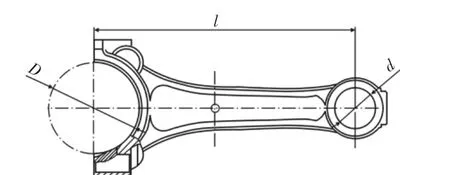
图4 发动机连杆的结构模型Fig.4 Structural Model of Engine Connecting Rod
以图4中的发动机连杆(材料为40Cr,弹性模量为211GPa,泊松比为0.277)为例进行实验分析,进行分析时省略连杆盖,只考虑连杆体。连杆的受力为循环交变载荷,其受载情况非常复杂,为了更好地分析连杆大小头的受力情况,选取连杆的最大压缩工况进行研究。在最大压缩工况时,连杆受到的压力最大,小头内圆的受力部分为靠近杆身一侧的半圆。为了简化问题,对杆身上的半个大头孔圆柱面进行全约束,半个小头内圆加载固定载荷。在一定范围内:D∈[55,70],d∈[20,35],l∈[210,230],F∈[10,35],改变连杆的设计参数和载荷大小,导出连杆的应力循环次数,得到7组实验数据[12],如表1所示。
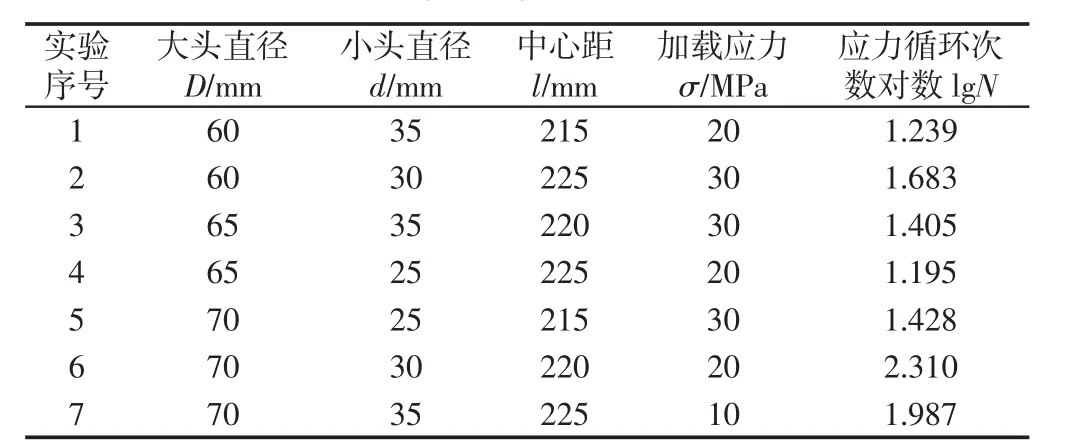
表1 实例优化结果Tab.1 Example Optimization Results
根据上文的分析,设相似结构连杆的性能相似目标函数可表达为:
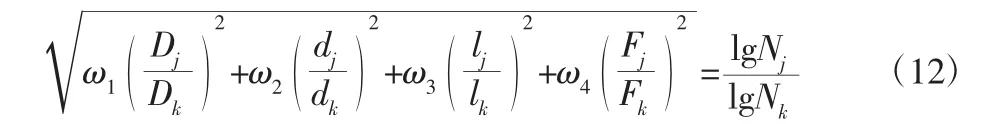
式中:j,k∈{1,2,3,4,5,6,7}且 j≠k,棕1、棕2、棕3、棕4—权重系数。
令(j,k)=(1,2),(1,3),(1,4),…,(6,7),代入式(12)得到一个方程组。对于该过约束方程组,用最小二乘法进行拟合近似求解,可求出近似解为:

为了验证上面的结果,增加4组附加实验,如表2所示。

表2 附加验证实验Tab.2 Additional Validation Experiments
将上述实验数据代入式(12)进行验证,计算得相对误差,如表3所示。由表3可知,通过相似分析模型得到的服役寿命与仿真实验结构之间的平均相对误差为8.24%,表明在可允许误差范围内,性能相似分析模型可以被用于相似结构的优化设计。

表3 实验数据分析Tab.3 Experimental Data Analysis
5.2 实例验证
汽车在不同路面行驶时,功率和连杆转速时刻发生变化,所以很难用一个准确的数值说明服役周期内连杆的转数。基于文献[13],将汽车的行驶里程数(再制造时间点)转换成车轮的转数,再通过减速比将车轮转数转换成连杆服役周期内的当量负载循环次数:

按车轮直径D=0.6m,总体减速比C=4.74计算得连杆主动再制造时间点的当量负载循环次数为:N2=1.313×109。
现通过改变连杆的设计参数来调整其再制造时间点。通过查阅相关资料与设计手册,已知某连杆初始中心距为230mm,优化前的再制造时间点为N1=1.17×109;优化后的再制造时间点为N2即主动再制造时间点,其他参数保持不变,如表4所示。

表4 实例验证Tab.4 Case Validation
根据上文的结论,将表中的两组数据代入连杆的性能相似公式:

解得:l=210.93mm。
为了验证以上结果,将优化后的连杆数据进行仿真实验分析,得负载循环次数=1.368×109,根据式(13)计算得优化后的主动再制造时间点为:

两者相对误差为4.21%,在可接受范围之内。
综上可知,若该连杆的中心距l由230mm缩短为210.93mm时,则其再制造时间点变为54.40万公里,非常接近于主动再制造时间点52.20万公里,满足了主动再制造时域要求,达到了发动机连杆优化设计目标的要求。
6 结论
(1)从主动再制造时域决策的角度提取出产品的主动再制造设计需求,阐释结构相似的概念与内涵,分析了零件结构与其相应性能演化之间的映射关系,基于文献及实验数据统计,构建性能相似性分析模型。(2)以发动机连杆为例,分析了产品服役过程中不同设计参数与载荷下的疲劳寿命,并通过对实际产品的优化设计说明了方法的有效性。(3)该方法具有可推广性,但要建立完整的分析模型需要对其他产品的设计参数、载荷与性能的关系进行逐一研究。因此,后续工作将通过优化设计参数及载荷的选取来减少有限元仿真和试验的工作量。
