操作状态下板式塔自振频率的影响因素

张 平 ，秦 然 ，张 静 ，吴剑华

（1．沈阳化工大学机械工程学院，辽宁 沈阳 110142；2．沈阳化工大学辽宁省化工新技术转移推广中心，辽宁 沈阳 110142）

1 引言

高达几十米甚至上百米的塔装置一般都设置在露天，露天放置的塔设备进行设计计算时，除考虑其所承受的操作压力、自重、地震载荷等作用之外还必须考虑风载荷的作用[1]。风载荷属于动力载荷，其使塔体产生加速度从而引起塔体结构的共振，共振过程中结构的位移和内力随时间而变化[2]。塔设备的自振频率是研究其振动特性的前提条件，是塔器动力计算的基础。对于等直径、等厚度的塔设备，其自振频率可按质量均匀分布的悬臂梁作横向振动进行计算[3]。计算塔设备自振频率的方法很多，如解析法、集中质量法、传递矩阵法及有限元法等[4]。文献[5]利用普洛尔法讨论了几种结构不同塔设备的自振特性，计算时考虑支撑形式的不同，其结论可用于指导塔设备的防振设计。文献[6]研究了直立锥形塔器在自重作用下的稳定性和自振特性，得出塔的锥度和截面形状对振动频率有很大影响。文献[7]利用传递矩阵法求解了悬挂塔的自振频率，计算结果与有限元法的计算结果相比，平均误差为（0.54～1.04）%。文献[8]研究塔设备固有频率时考虑了塔体厚度的影响，并计算了塔设备的不平衡响应振幅。文献[9]计算了结构载荷分布、约束条件复杂的等截面及变截面直立塔设备的自振频率。变截面塔的一阶自振频率分别用有限元法[10]和图解法[11]进行了分析和讨论。文献[12]将板式塔工作过程中的液体动力载荷作为预应力，将气体载荷等效为激励载荷，分析了板式塔的动态特性。以多万向节陀螺为阻尼器，对风荷载和地震作用下塔架结构进行动力控制[13]。文献[14]对吸收塔的结构进行了模态分析与振型研究。文献[15-16]研究塔设备的动力特性时，利用了有限单元法。

实际生产操作状态下的板式塔，塔板上存在着一定高度的液态操作介质，由于介质的流动性，操作介质的重心是不断变化的。因此，板式塔的质量沿其轴线方向是非均匀分布的，计算操作状态下板式塔的自振频率时，利用对分布质量进行聚集的传递矩阵法更为合适[17]。

考虑塔板上操作介质流动而产生的偏心惯性力矩，得到的偏心惯性力矩传递矩阵同卓存真[18]提出的普洛尔传递矩阵相比，增加了一项与板式塔结构参数有关的偏心惯性力矩项。利用MATLAB程序，通过计算四种不同结构参数的板式塔，比较了解析法和普洛尔传递矩阵法计算板式塔自振频率的误差大小，比较了偏心惯性力矩传递矩阵法和普洛尔传递矩阵法的计算误差。探讨了塔板直径、塔板上介质液层高度以及介质密度对偏心惯性力矩传递矩阵法计算操作状态下板式塔自振频率的影响。

2 自振频率的计算方法

2.1 解析法

解析法计算板式塔的自振频率，认为板式塔质量沿塔体均匀分布[3]，第一阶自振频率为：

式中：fa1—解析法第一阶自振频率/s-1；H—板式塔的总高度/m；m—板式塔的总质量/kg；E—塔体材料的弹性模量/MPa；I—塔体截面的惯性矩/m4。

解析法计算高阶自振频率与第一阶自振频率的关系为：

式中：i—自振的阶数；fai—解析法第i阶自振频率/s-1。

2.2 普洛尔传递矩阵法

文献[18]提出计算板式塔自振频率的普洛尔传递矩阵，没有考虑塔板上操作介质的流动性，认为塔体振动时操作介质重心始终位于塔体的轴线上，只是单纯地把板上操作介质作为固体与塔体质量一同计算。普洛尔传递矩阵法的一个计算单元Kbi为：

式中：Kbi—普洛尔传递矩阵计算单元；m1i—第i段板式塔质量/kg；fb—普洛尔传递矩阵法自振频率/s-1。

2.3 偏心惯性力矩传递矩阵法

文献[17]研究操作状态下板式塔的自振频率时，考虑塔体振动时，塔板上操作介质的流动性，提出介质对塔体产生额外的偏心惯性力矩。偏心惯性力矩传递矩阵法的一个计算单元Kci为：

式中：Kci—偏心惯性力矩传递矩阵计算单元；m1i—第i段板式塔质量/kg；m2i—第i段塔板上操作介质质量/kg；D—塔板直径/m；hL—塔板上液层高度/m。

偏心惯性力矩传递矩阵，比普洛尔传递矩阵多增加一项与板式塔直径、板上操作介质高度及操作介质质量相关的偏心惯性力矩项。

3 操作状态下板式塔的参数

3.1 板式塔结构参数

选取了四种结构不同的板式塔[3、19]进行实例计算，探讨塔板直径、板上操作介质液层高度及介质密度对板式塔各阶自振频率的影响。设定距地面10m处单位长度的风载荷为300N/m，塔体材料的弹性模量为1.96×1011Pa。板式塔的结构及板上操作介质参数，如表1所示。

表1 板式塔的结构及介质参数Tab.1 Structure and Medium Parameters of Tray Column

3.2 板式塔操作和物料质量

文献[3、19]中四个板式塔在操作状态下，塔板上的操作介质质量、塔体自身及内构件组成的结构质量，如表2所示。

表2 板式塔的操作介质质量及结构质量Tab.2 Operating Liquid and Structural Quality of Tray Column

4 自振频率的误差分析

利用解析法、普洛尔传递矩阵法及偏心惯性力矩传递矩阵法分别计算表1中四个板式塔的前10阶自振频率。

4.1 解析法和普洛尔传递矩阵法的比较

定义解析法和普洛尔传递矩阵法的结果误差为：

解析法和普洛尔传递矩阵法的计算误差曲线，如图1所示。图中可以发现，四个塔设备前10阶振型的自振频率误差变化不大，只有第二阶振型的自振频率误差相对较大，比其它阶振型高出10%。a塔和d塔的误差较小，低于1%，c塔的最大误差是1.99%，b塔的最大误差为3.38%。通过表2观察，a塔和d塔的长径比分别为46和30.5，b塔和c塔的长径比分别为13.5和16。说明长径比较大的板式塔可以认为塔体质量沿塔体均匀分布，而长径比较小的板式塔不适合利用解析法计算自振频率。

图1 解析法和普洛尔传递矩阵法的比较Fig.1 Comparisons between Analytical Method and PROHL Method

4.2 普洛尔传递矩阵法和偏心惯性力矩传递矩阵法的比较

普洛尔传递矩阵法和偏心惯性力矩传递矩阵法的计算误差为：

利用式（4）计算板式塔的自振频率时，增加了一项与塔板直径和板上液体介质质量有关的偏心惯性力矩项，即塔体振动时液体介质产生的额外偏心惯性力矩。普洛尔传递矩阵法和偏心惯性力矩传递矩阵法的计算结果误差曲线，如图2所示。

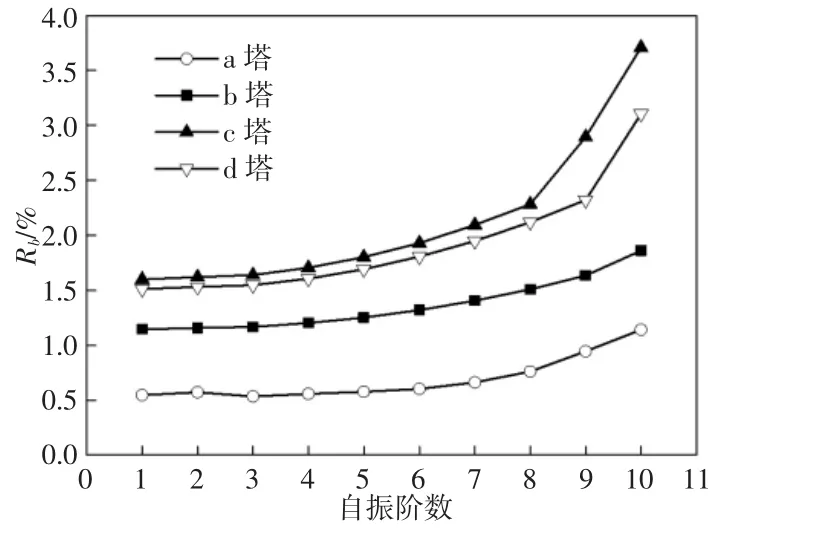
图2 普洛尔传递矩阵法和偏心惯性力矩矩阵法的比较Fig.2 Comparison of PROHL Transfer Matrix Method and Eccentric Inertial Moment Matrix Method

由图2可知，随着自振阶数的增加，计算误差增加，尤其对八阶振型以上的振型，计算误差较大。a塔的误差最小，小于1%，b塔的平均误差为1.2%左右，最大误差1.86%。c塔和d塔的平均误差为2%左右，最大误差分别为的3.71%和3.11%。通过分析表1可以看出，c塔和d塔的直径大于a塔和b塔，说明塔板直径大的板式塔应该考虑额外偏心惯性力矩的影响。

5 操作介质质量和塔板直径对自振频率的影响

5.1 塔板直径对自振频率的影响

板式塔一阶自振频率随塔板直径增量变化的曲线，如图3所示。可以发现，随着塔板直径的增加，b塔的自振频率基本不变，a塔、c塔和d塔的自振频率都呈下降的趋势，d塔的变化最为明显，直径增加一倍，自振频率也基本增加一倍。由表1、表2可知，b塔的塔高为18.9m，长径比为13.5；d塔的塔高为73.3m，长径比为30.5，说明塔板直径变化对长径比大的高塔的自振频率影响较大。因为d塔的塔体高，塔板多，塔板直径的变化对操作介质质量影响较大，故对自振频率影响较大。

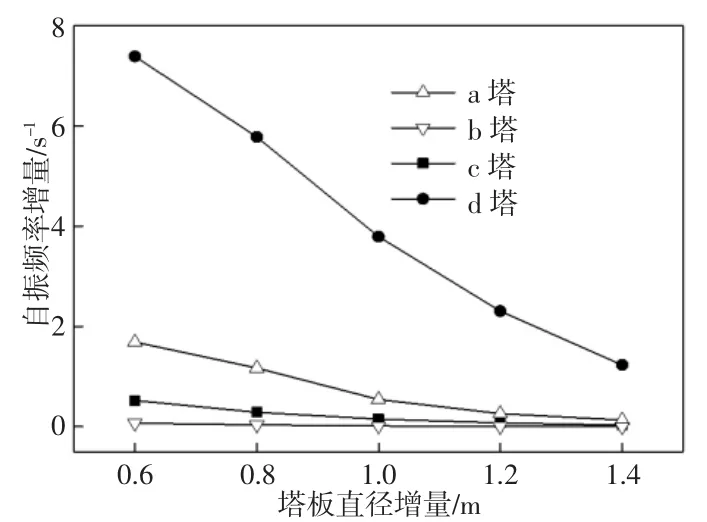
图3 直径增量对塔体自振频率的影响Fig.3 Effect of Diameter Increment on Natural Vibration Frequency of Column

5.2 介质液面高度对自振频率的影响

图4 液面高度对各阶振动频率的影响Fig.4 Effect of Liquid Level Height on Vibration Frequencies of Different Orders

当塔板溢流量发生变化时，塔板上的液面高度也随之变化。板式塔操作介质液面高度对各阶自振频率的影响，如图4所示。可以发现，一阶、四阶以及八阶自振频率随操作介质液面高度增加略有增加。介质液面高度增加一倍，四个板式塔自振频率增加的百分比，如表3所示。表中可以看出，c塔变化最大，一阶、四阶以及八阶自振频率分别增加13.2%，14.3%，16.2%。随着液面高度增加，操作介质质量增加，自振频率降低，但通过式（4）可知，液面高度与自振频率成正比，两者抵消，液面高度变化对自振频率影响不大。

表3 各阶自振频率的增加比率Tab.3 Increase Ratio of Natural Frequency of Each Order

5.3 介质密度对自振频率影响

板式塔的一阶自振频率随操作介质密度的变化曲线，如图5所示。分析图形发现，随着介质密度的增加，板式塔的自振频率呈下降的趋势，对c塔的影响比较大，其他3个塔下降的比较平缓，c塔介质密度增加一倍时，自振频率下降50%。

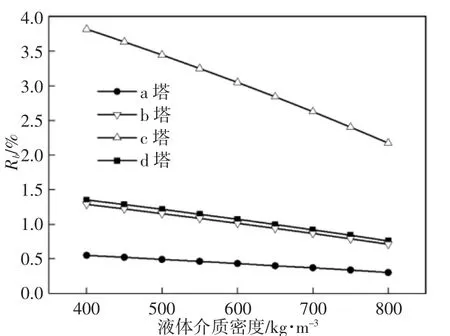
图5 液体介质密度对自振频率的影响Fig.5 Effect of Liquid Medium Density on Natural Frequency

图6 各阶振动频率随液体介质密度的变化Fig.6 Variation of Vibration Frequencies of Each Order with Density of Liquid Medium

针对表1中b塔各阶自振频率随操作介质密度增加的变化。可以发现，随着操作介质密度的增加，各阶自振频率都呈下降的趋势，阶数越高，下降的幅度越大，如图6所示。介质密度增加一倍，一阶自振频率下降50%，九阶自振频率下降一倍。操作介质密度的增加，增加了板式塔的操作介质质量，降低了塔体的自振频率，c塔的D2/（12HL）最大，故操作介质密度的变化对c塔的影响最大。

6 结论

（1）大长径比的高塔，解析法和普洛尔传递矩阵法的计算误差较小。长径比大的板式塔可以认为塔体质量沿轴线均匀分布，而长径比小的板式塔不适合利用解析法计算自振频率。

（2）塔板直径大的板式塔进行动力计算，核算塔体自振频率时，应该考虑板上操作介质的额外偏心惯性力距的影响。塔板直径增加，塔体自振频率减小，对自振频率影响比较大，不能忽略。

（3）操作介质液面高度增加，塔体各阶自振频率增加，但影响不大，可以不用考虑。操作介质密度增加，塔体各阶自振频率减小，长径比小的塔体应该考虑介质密度的影响，尤其对于高阶自振频率。