基岩与进水塔的相互作用对塔体的地震损伤影响研究
2022-06-21张云涛段锡志郭书亮郑晓东
张云涛,段锡志,郭书亮,郑晓东
(1.河北省水利工程局集团有限公司,河北 石家庄 050021;2.河北工程大学水利水电学院,河北 邯郸 056038;3.重庆工贸职业技术学院,重庆 408000)
0 引 言
进水塔是引水、泄水系统的控制性水工建筑物,它的安全性对整个引水、泄水系统甚至大坝的安全都有着举足轻重的作用[1-3]。对于如此重要且条件复杂的高耸结构,很多学者在其稳定性方面开展了大量的研究[4-8]。曹伟[9]对于进水塔在强震作用下局部混凝土进入塑性阶段产生破坏,建立混凝土拉压弹塑性本构关系,考虑混凝土材料的非线性对进水塔进行非线性时程分析。陈震等[10]模拟在强震作用下进水塔内部累计损伤导致的塔体变形,引入损伤弹塑性模型,对混凝土材料非线性进行研究分析。唐青山等[11]采用有限差分法分析了回填过程混凝土和边坡的稳定性,主要考虑了回填混凝土与边坡接触面(岩-混凝土接触面)的相互作用。李骞等[1]针对地震作用下应力释放,考虑塔体线弹性材料,引入动态接触方法和弹性连接研究了局部接触非线性问题,说明了考虑局部接触非线性的必要性。但是,专家们分析高耸结构与地基岩体之间的相互作用时,该结构均按弹性材料进行分析。
塔体与岩体基础之间的动力相互作用和材料非线性是影响进水塔抗震稳定性的2个重要因素。对于进水塔结构抗震问题,大多数研究都单一的考虑材料非线性因素的影响或者接触非线性因素的影响,这样对实际进水塔的结构和受力情况都不能够准确来描述。因此,为了更加接近进水塔的真实实际情况,本文在考虑进水塔材料非线性的基础上,研究羊曲进水塔在地震荷载作用下塔体与岩体基础之间的动力相互作用,利用面-面接触单元模拟进水塔塔体与基岩各个面之间的接触非线性特性,分析地震动持续作用下塔体顶部相对位移、塔体结构的损伤过程以及塔体与基岩之间的接触状态,从而为进水塔的设计提供科学依据。
1 工程实例与有限元模型
1.1 工程概况及参数的选取
本文运用ABAQUS建立了羊曲进水塔的塔体-地基有限元模型(如图1所示),钢筋本构采用随动强化模型。进水塔中的钢筋采用三维线单元,镶嵌到混凝土中,钢筋与混凝土之间没有滑动。地基的宽度在塔的左岸、右岸各取28.0 m;塔前后各取40.0 m;深度取接近于塔体高度的1倍,即80.0 m;围岩按照地基宽度取28.0 m。
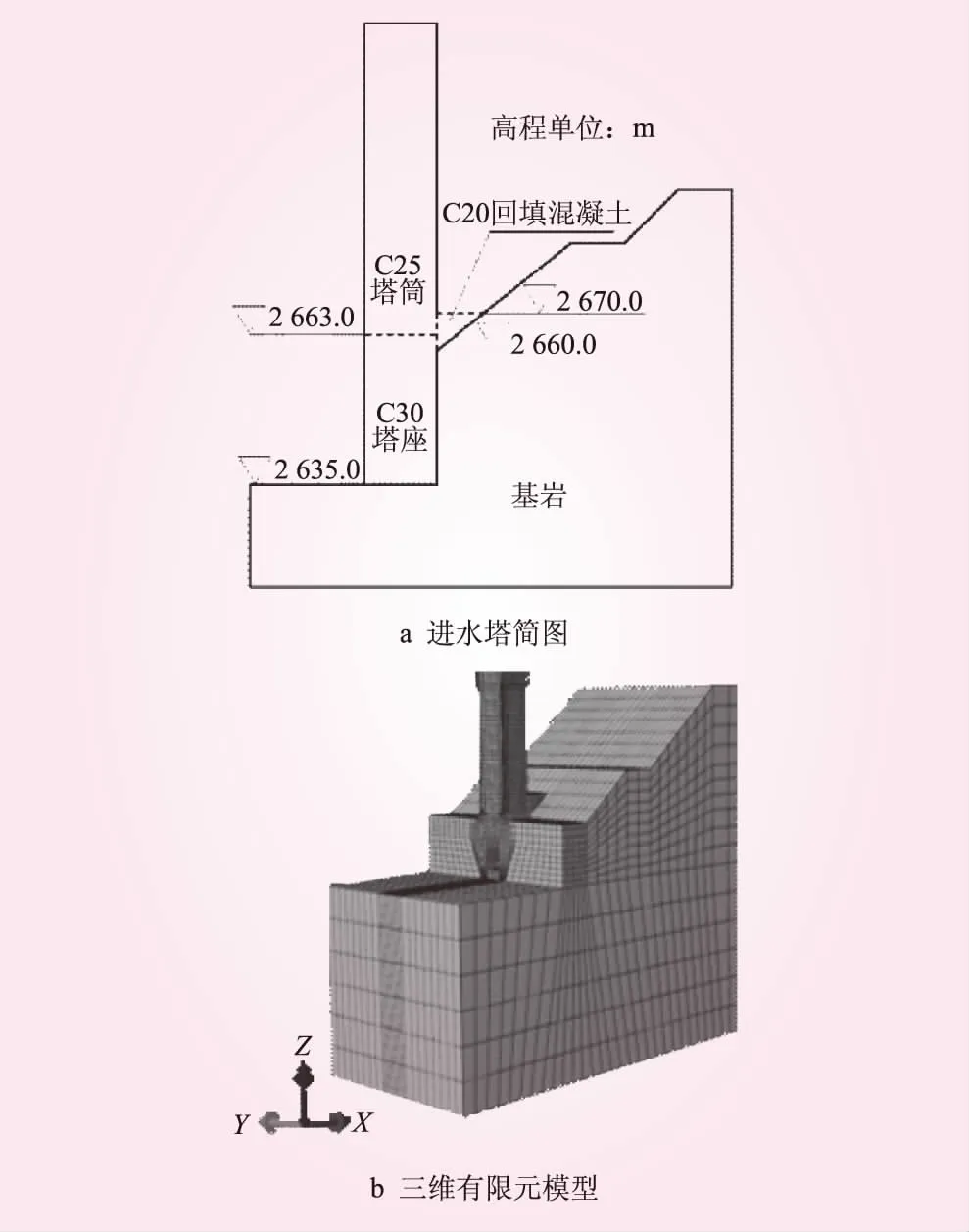
图1 进水塔塔体-地基整体模型示意
1.1.1 塔体混凝土材料
羊曲进水塔塔座(2 663.00 m高程以下)混凝土强度等级为C30;塔筒(2 663.00 m高程以上)混凝土强度等级为C25;塔后回填混凝土强度等级为C20,见图1a,混凝土材料动态弹性模量值按照GB 51247—2018《水工建筑物抗震设计规范》确定,相应的材料系数较静态标准值提高50%,动态抗拉强度值较静力参数增加20%,混凝土材料具体参数见表1。

表1 混凝土有关材料参数
1.1.2 基岩材料参数
羊曲进水塔地基岩体以Ⅱ类中厚层砂岩为主,坚固系数为10。地基岩体的密度为2 720 kg/m3,地基变形模量为15 GPa,泊松比为0.167,摩擦系数为1.07,黏聚力取值为2 MPa,断裂能为82 N/m。
1.1.3 塑性损伤模型
郭胜山[12]在Lee and Fenves基础上建立了考虑损伤引起的不可恢复残余变量的塑性损伤模型,塑性损伤模型本构关系如图2所示。
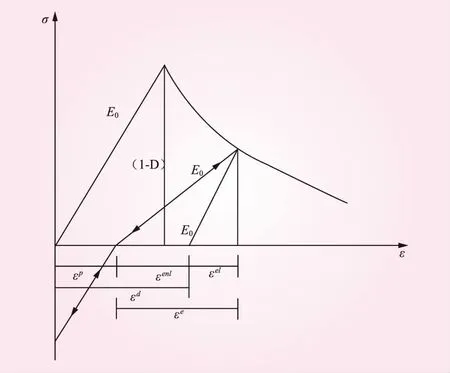
图2 塑性损伤模型本构关系
图2中的塑性损伤模型本构关系为
ε=εe+εp
(1)
εe=εel+εenl
(2)
εd=εp+εenl
(3)
式中,ε为总应变量;εe为弹性应变;εP为不可恢复残余应变;εel为初始弹性应变;εenl为刚度减小引起的非弹性应变;εd为损伤应变。
塑性损伤模型应力应变关系
本构关系σ=(1-d)D(ε-εP)
(4)

(5)
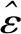
损伤演化关系为
(6)
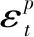
1.2 荷载
主要考虑的荷载有静水压力,动水压力,扬压力,塔体自重和地震荷载等。动水压力采用GB 51247—2018《水工建筑物抗震设计规范》中附加质量模型进行计算。对进水塔考虑3个方向的地震荷载作用,本文通过极限抗震能力计算,确定出2倍的设计地震是羊曲进水塔“破坏”前的最大地震荷载[13],即地震峰值加速度为0.608g。调整后的人工波作为设计人工地震波如图3所示。

图3 设计人工地震波
1.3 接触力学模型
接触非线性属于强非线性问题,接触状态分为张开、粘结、滑移等[14]。本文运用面-面接触方法来模拟进水塔塔底板面与基岩、以及进水塔塔后回填混凝土部分与基岩之间的接触非线性。在进水塔结构和基岩受力面的法向方向设置为硬接触,受力面的切向方向设置库伦摩擦系数。
1.3.1 接触面约束条件
(1)法向接触条件[9]。①法向的不可惯入性,假设接触面上点A、B的坐标分别为uA、uB,定义点A指向点B的法向矢量为n,定义两点方向距离为dn,则dn=(uA-uB)n,若dn>0,表示分离;若dn<0,表示相互侵入;若dn=0,表示接触状态。②法向不贯穿条件为dn=(uA-uB)n≥0。
(2)切向接触条件[9]。定义两点接触力中切向接触力为λs,以库伦模型考虑摩擦,定义界面摩擦系数为μ。当两点处于接触状态时,若|λs|=μλn表示两点将发生滑移;若|λs|<μλn处于粘结状态。即
粘结状态
(7)
滑移状态
(8)
1.3.2 罚函数接触模型
罚函数法是基于罚函数定义切向行为的库伦摩擦准则。罚函数可满足法向不嵌入条件,罚函数摩擦允许接触面有弹性滑移,能够有效处理过约束问题,适用于大多数的接触问题,本文选用罚函数法。通过式(9)来定义临界剪应力与接触压力之间的关系,即
τcrit=μp
(9)
式中,τcrit为材料的剪切屈服应力;p为接触面间接触压力;μ为摩擦系数。接触单元目标单元几何形状为矩形,初始接触状态为闭合状态。
2 计算分析
2.1 进水塔结构自振特性
通过对进水塔结构的自振特性进行分析求解水塔结构的动力特性,运用ABAQUS有限元分析软件进行模态分析可以得到结构的自振周期和自振频率。羊曲进水塔的前5阶的自振频率如表2所示。

表2 进水塔自振频率
进水塔结构阻尼采用瑞利阻尼,取进水塔前5阶振型频率,阻尼比取7%,计算得到的满库情况的瑞利阻尼参数α=0.152 4;β=0.032。
2.2 接触状态分析
在地震荷载作用下,对进水塔与基岩之间的接触状态进行分析,塔体底板面、塔体后面、回填混凝土部分和塔体左右面与基岩接触面状态云图如图4、5所示。
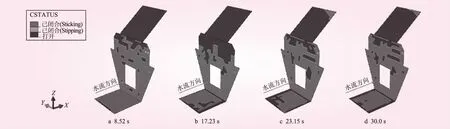
图4 塔体底板面、塔体后面和回填混凝土与基岩接触面状态云图
由图4中塔体底板面与基岩接触面状态云图可知,在地震荷载作用下,8.52 s时进水塔塔体底板面与岩基之间接触面首次被拉裂。在塔体x向位移最大时刻(17.23 s),最大接触压力出现在底板底面靠上游处,塔体底板面与岩基之间后部分接触面处于张开状态,张开值随着位移值的逐渐增加从塔体与基岩接触面的左侧到右侧呈现逐渐递增。在y向最大位移最大时刻(23.15 s),最大接触压力出现在底板底面靠上游处,塔体底板面与岩基之间接触的薄弱面处于张开状态。张开值从塔体与基岩接触面的左侧到右侧呈现递减。
由图4中回填混凝土与基岩接触面状态云图可知,在地震荷载的持续作用下,在8.52 s和17.23 s,塔后回填混凝土与基岩之间处于完全张开状态。在23.15 s和30.0 s,塔体被完全贯穿破坏等时间点,其接触面右侧有小部分处于闭合接触状态。
由图4中塔体后面基岩接触面状态云图可知,在8.52、23.15、30.0 s,塔体被完全贯穿破坏等时间点塔体后面基岩接触面张开状态变化几乎相同,在塔体x向位移最大时刻(17.23 s),塔体后面与基岩接触面张开状态增大。造成以上两种现象是由于在考虑塔体-基岩体系和塔后回填混凝土-基岩之间存在接触非线性,他们之间通过摩擦系数和黏聚力约束,在静、动荷载的持续作用下,塔后回填混凝土与基岩之间处于完全张开状态。随着x向地震强度的逐渐增加,使塔体在x向有较大的前倾。
由图5可知,塔体在x向最大位移时刻(17.23 s)和y向最大位移最大时刻(23.15 s)左面处于张开状态的面积大于右面,左侧面在17.23~23.15 s之间处于张开状态的面积呈现逐渐递增。张开状态的位置主要处于接触面的上半部分的大部分面积。

图5 塔体左右面与基岩接触面状态云图
2.3 塔顶位移响应分析
考虑塔体-基岩体系之间有可靠的连接,不考虑接触非线性和考虑接触非线性两种情况,分别对进水塔结构进行时程分析,同时输入3个方向的地震荷载,分析塔体在地震荷载作用下塔顶相对位移随时间变化的规律,得到塔顶相对位移时程曲线,如图6所示。

图6 塔体顶部相对位移时程曲线
由图6a可知,塔体x向相对位移时程曲线在14.0 s左右出现明显变化。不考虑接触非线性情况下塔体顶部发生的相对位移幅值为65.11 mm。考虑接触非线性情况下,塔体x向的相对位移幅值为85.37 mm,与不考虑接触非线性相比,考虑接触非线性时塔顶最大位移幅值增加31.12%。这是由于塔体与基岩之间不考虑接触非线性情况时,将塔体、塔后回填混凝土与周围岩体作为一个整体进行研究,塔体和塔后回填混凝土相接触部分容易产生应力集中现象,导致塔体产生损伤开裂,使塔体x向产生较小的位移幅值。考虑塔体、塔后回填混凝土与基岩之间存在接触非线性,接触面间主要是通过摩擦力来减小塔体顺水流方向的位移,当动静荷载的叠加作用力大于摩擦阻力的时,塔后回填混凝土与基岩之间的接触面局部就会处于张开状态,使得塔体在顺水流方向产生较大塔顶相对位移。
由图6b可知,考虑塔体与基岩间存在接触非线性和不存在接触非线性两种情况,塔体顶部相对位移变化趋势几乎同步,这是由于在两种情况下,垂直水流y向上塔体与岩基之间都受法向应力的约束作用,塔体与基岩之间的接触面处于闭合状态,因此,使塔体顶部发生相对位移变化趋势几乎同步。
由图6c可知,考虑塔体与基岩之间接触非线性和不考虑接触非线性两种情况下,塔体在地震荷载加载初期,两种情况下的塔顶位移变化基本是一致的,从14.0 s前后塔顶相对位移出现逐渐递增趋势,考虑接触非线性时相对位移递增速率更快,25.0 s左右塔顶相对位移达到最大值。考虑接触非线性情况下塔体顶部最大相对位移值约为38.00 mm,不考虑接触非线性情况下塔体顶部最大相对位移值为17.0 mm,考虑接触非线性情况下相对于不考虑接触非线性情况下最大位移值增长123.52%。这是由于地震荷载加载初期,荷载强度较小,塔体处于弹性阶段,所以两种情况下初期塔顶相对位移的变化基本是一致的。随着地震作用的逐渐加强,在不考虑接触非线性情况下,将塔体-基岩体系看做一个整体,塔体z向相对位移小,而考虑接触非线性情况下,塔体与基岩之间的接触面局部处于张开状态,增大了塔体z向相对位移。
2.4 进水塔塔体拉损伤过程分析
假设塔体与基岩之间有可靠的连接,不考虑非线性接触情况和考虑塔体与基岩之间存在非线性接触两种情况计算得到的塔体腰部损伤云图如图7所示。
由图7可知,在不考虑接触非线性情况下,进水塔塔体在高程2 663.0 m出现贯穿损伤区域,该区域为不同混凝土材料交接面处,其扩展方向从上游到下游。在考虑接触非线性情况下,塔体损伤区域包括高程2 663.0 m混凝土材料交界面处和引水隧洞上表面几何突变处。在考虑接触非线性条件下损伤突变比不考虑接触非线性损伤突变损伤破坏单元要多,塔体腰部损伤在在某一时间段内呈现突发性的增长,总损伤程度在某一时间段逐渐累积。造成这一现象的主要原因是进水塔塔体与基岩之间的相互作用,扩大了地震能量,增加了塔体的实际损伤开裂。

图7 进水塔拉损伤发展过程演化
图8为进水塔损伤耗散能时程曲线。由图8可知,进水塔-岩基系统在地震荷载作用下被完全贯穿损伤破坏,考虑接触非线性模型计算的损伤耗散能为171 758.0 J,不考虑接触非线性模型计算的损伤耗散能为113 251.0 J,考虑接触非线性情况相对于不考虑接触非线性情况下的损伤耗散能增长了34.06%。
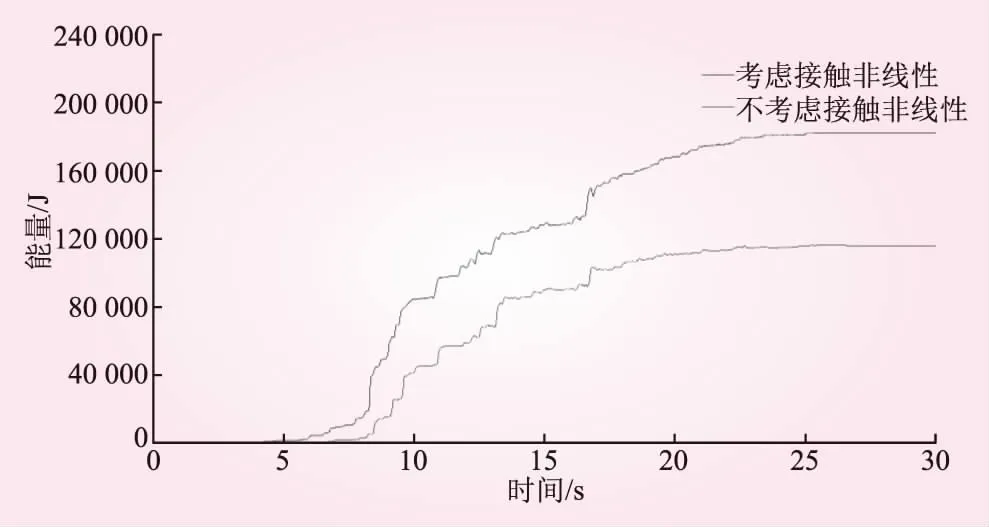
图8 进水塔损伤耗散能时程曲线
综上所述,进水塔-基岩体系在地震荷载作用下,不考虑接触非线性情况,塔体损伤破坏比较慢,损伤单元较少;考虑接触非线性情况,扩大了地震能量,塔体损伤破坏比较快,损伤单元较多。因此,考虑接触非线性情况下,进水塔损伤模型偏不安全,但是进水塔模型更加接近真实实际,可以为进水塔及相近高耸混凝土建筑的设计提供更加合理的建议。
3 结 论
本文在考虑塔体材料非线性的基础上,通过对比分析进水塔与基岩之间考虑接触非线性和不考虑接触非线性2种方案,得到如下结论:
(1)在不考虑接触非线性情况下,进水塔在塔后回填混凝土部分会产生应力集中现象,塔体-基岩体系在应力集中的影响下损伤单元主要集中于不同混凝土材料交界面处。考虑塔体与基岩之间存在接触非线性,无应力集中现象产生,塔体损伤主要集中于不同混凝土材料交界面处和引水隧洞上表面几何突变处。
(2)通过对塔体位移、损伤、能量等方面的分析,相对于不考虑接触非线性情况下,考虑接触非线性情况的塔顶最大相对位移幅值增加了31.12%,塔体的损伤区域扩大,损伤耗散能增长了34.06%,这是由于考虑进水塔塔体与基岩之间的相互作用,扩大了地震能量,增加了塔体的实际损伤开裂。
(3)考虑进水塔与基岩接触非线性的情况下,进水塔模型偏不安全,但是该情况下进水塔模型更接近于真实情况,可为进水塔设计提供更加合理的建议。随着地震强度逐渐增大,进水塔与基岩基础面会产生局部瞬态拉裂,为提高建筑物的稳定性,可在开裂部位进行适当配筋。该研究成果对实际工程设计具有一定的指导意义。
