二维结构拓扑优化的GPU并行计算方法研究

刘家彤 ，王春洁 ，2，吴 健 ，付志方

（1.北京航空航天大学机械工程及自动化学院，北京 100191；2.北京航空航天大学虚拟现实技术与系统国家重点实验室，北京 100191）

1 引言

拓扑优化致力于在设计域内找到最优结构，使得结构在满足给定约束条件的情况下具有最佳的工作性能[1]。自从文献[2]对这一问题进行研究开始，拓扑优化已经在多个领域得到研究应用，包括结构刚度最大化设计[3-4]、柔性机构设计[5-6]等。尽管拓扑优化在过去几十年得到了广泛的应用，但由于进行拓扑优化时涉及结构有限元分析、大规模线性方程组的求解和结构单元灵敏度求解等复杂计算过程非常费时，提高计算效率是拓扑优化设计中急需解决的重要问题之一。

由于其优化过程稳定，固体各项同性材料惩罚法（Solid Isotropic Material with Penalization，SIMP）是结构拓扑优化中常用的方法之一，经过学者的努力，已经应用于解决各种优化问题[7-8]。为了方便其应用研究，文献[9]给出了SIMP方法的MATLAB实现代码，俗称“99”行代码，然而其迭代过程需要重复计算刚度矩阵导致其计算效率较低。因此，文献[10]对其进行改进，提出了“88”行代码，从而提高了计算效率。但是，对于大型结构优化问题，“88”行代码计算能力尤显不足，仍需要开发更加高效的算法。

GPU计算是由CPU和GPU协同工作实现的，CPU用于控制计算过程和实施存储策略，而具体的计算过程则由GPU进行[11]。CUDA（Compute Unified Device Architecture）是NVIDIA 推出的通用并行计算架构。利用CUDA可以直接操作GPU内存，从而使得GPU能够进行除图形处理之外的其他一般化应用[12-13]。由于GPU计算计算过程高度并行化，使得大规模的计算能够在较短时间内得到结果，近年来得到了广泛的应用和发展[14]。

基于GPU计算，以SIMP法进行结构拓扑优化为例，利用CUDA对其进行并行化改进，给出了一种GPU并行计算拓扑优化方法，并与现有计算方法进行了比较。

2 基于SIMP法的拓扑优化方法

2.1 问题描述

基于SIMP法的拓扑优化方法以单元密度ρe作为设计变量，在优化过程中通过改变各单元密度大小来获得最小的结构柔度，其数学模型如下：

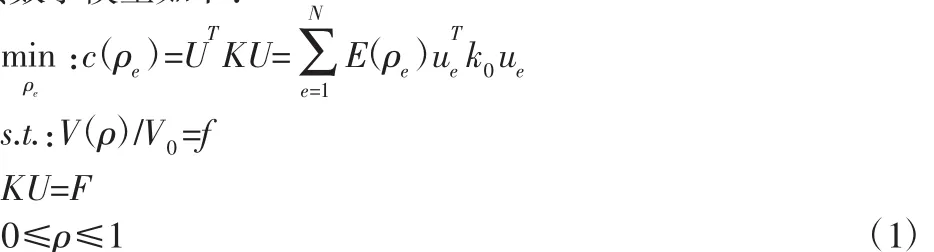
式中：c（ρe）—结构柔度；U、F—结构位移向量和加载的力向量；K—结构总体刚度矩阵；ue—单元位移向量；k0—单位杨氏模量下的单元刚度矩阵；N—设计域的划分单元数；ρ—由单元密度组成的设计变量向量；V（ρ）、V0—材料体积和设计域体积；f—给定的结构体积分数。

为了防止单元密度变为零，导致刚度矩阵奇异的情况，采用约束最小刚度的插值模型[15]计算材料属性Ee，即：

式中：E0—材料的弹性模量；Emin—防止刚度矩阵奇异而赋予无材料单元很小的刚度值，p≥1是惩罚因子，取p=3。

2.2 优化算法

采用了优化准则法对优化问题进行求解，准则可表述为[16]：

式中：m—一个正的偏移量；η—数值衰减系数，中间变量Be表示如下：

其中拉格朗日乘子λ可由二分查找法确定，以满足体积约束要求。目标函数和材料体积对于单元密度的灵敏度可表示如下[10]：

2.3 过滤策略

为了保证拓扑优化过程的稳定性，需要对单元密度进行过滤，过滤方法如下[17]：

式中：Ne—给定过滤半径范围内的有限单元集合；驻（e，i）—当前单元e和目标单元i之间的中心点距离；rmin—过滤半径；He，i—由 驻（e，i）和 rmin所决定的权值。

3 算法实现

主要在结构有限元分析、灵敏度计算、单元密度过滤和优化更新阶段引入GPU计算，来实现对SIMP拓扑优化算法的加速。

3.1 有限元分析

针对2维平面拓扑优化问题，设计域为笛卡尔坐标系内的一个矩形区域，如图1所示。对其进行有限元划分，得到nelx×nely个矩形单元，每个单元包含四个节点，每个节点与四个矩形单元邻接（边界和顶点处，分别为1个和2个）。

图1 有限元网格划分Fig.1 Finite Element Mesh Generation

传统方法在进行有限元分析时，以单个单元为基础，先构建出一个单元的刚度矩阵Ke，通过装配得到整体刚度矩阵。为了通过GPU并行化计算对这一过程进行加速，有两种加速方案：针对单元的并行化处理及针对节点的并行化处理。针对单元的并行处理，即以单元为划分，针对每个单元进行刚度矩阵的组装，由于每个单元的节点可能分属于其他三个单元，对于其中任意一个节点需要将几个单元计算得到的值进行合成，这样就出现了在并行过程中的读写竞争问题，解决这一问题会引入其他计算而增加额外的计算时间。而针对节点的并行化处理只需一次计算得到节点处的刚度值，不存在读写竞争问题，因此在装配刚度矩阵时选择了该处理方式。

为了进一步说明以上两种处理方式的不同，其刚度矩阵装配示意图，如图2所示。图中左侧为任意一个单元，以顺时针方向对其节点进行编号，通过计算得到单元的刚度矩阵Ke，右图是以节点e为中心的四个单元，以左上的第一个单元为例，节点e位于相对左图中的3节点，对应了Ke中第5，6行的刚度值，对另外三个单元进行同样的分析，就针对节点e对刚度矩阵Ke进行了重组，即可将原本以单元为基础的刚度矩阵转变成为以节点为基础的刚度数组

图2 从单元到节点的单元刚度矩阵重组方式Fig.2 Reconstruction of Element Stiffness Matrix from Element Based to Node Based

3.2 GPU实现

图3 线程块网格划分Fig.3 Grid of Thread Blocks Partition

将文献[10]中刚度矩阵装配的计算时间和文本GPU计算方法刚度矩阵装配时间进行比较，测试结果，如表1所示。可以看出，采用节点刚度方法的GPU计算方法进行刚度矩阵计算速度得到了很大的提升，是文献[10]中算法的速度的（3～5）倍。为了更直观的表达，给出了两者测试时间的柱状图，如图4所示。

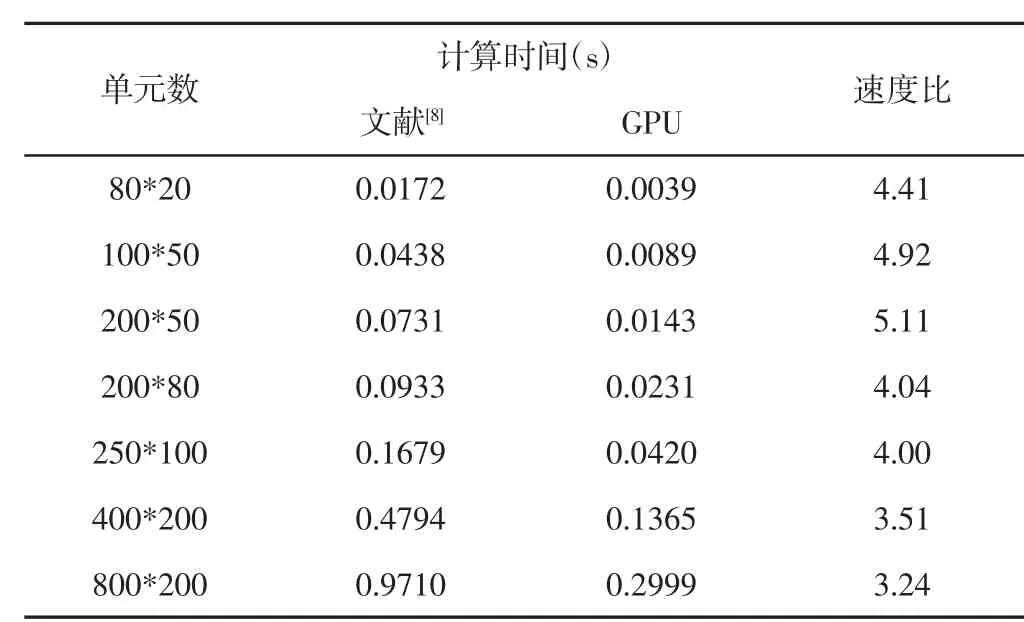
表1 刚度矩阵组装测试结果Tab.1 Test Results of Stiffness Matrix Assembly

图4 刚度矩阵装配效率比较柱状图Fig.4 Histogram of Algorithm Efficiency Comparison of Stiffness Matrix Assemble

4 数值算例

为了验证所述算法在结构优化设计中的效率，以SIMP法进行结构拓扑优化为例，对两端简支梁、悬臂梁两个算例分别进行优化。实现平台及硬件参数，如表2所示。

表2 算法实现平台及参数Tab.2 Algorithm Implementation Platform and Parameters

4.1 两端简支梁

对于两端简支的二维梁结构拓扑优化问题，如图5所示。根据对称性，可取其中一半进行优化处理。问题的设计域为400×100的矩形区域，左端边界x方向固定，右下角y方向固定，左上角加载方向向下的载荷F，材料需用体积为40%。分别采用文献[10]和提出的GPU计算方法以柔度为优化目标，对结构进行拓扑优化计算，得到优化结果，如图6所示。由图可知，所述的GPU计算方法可以得到与文献[10]算法相同的优化结果，证明了算法的有效性。

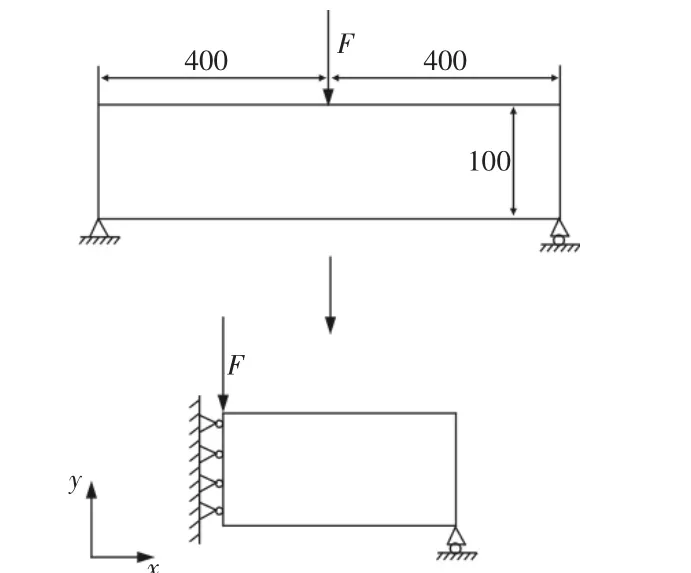
图5 两端简支的二维梁和问题简化图Fig.5 Two Dimentional Simplified Beam with Two Ends and Simplified Graph

图6 简支梁优化结果对比Fig.6 Comparison of Optimization Results of Simply Supported Beam

将算法和文献[10]的优化时间进行比较，结果，如表3所示。可以看出，算法计算速度得到了提升，是文献[10]中算法的速度的（1.5～2）倍，说明了算法的高效性。为了更直观的表达，给出了两算法计算时间的柱状图，如图7所示。

表3 简支梁算法效率比较Tab.3 Algorithm Efficiency Comparison of Simply Supported Beam

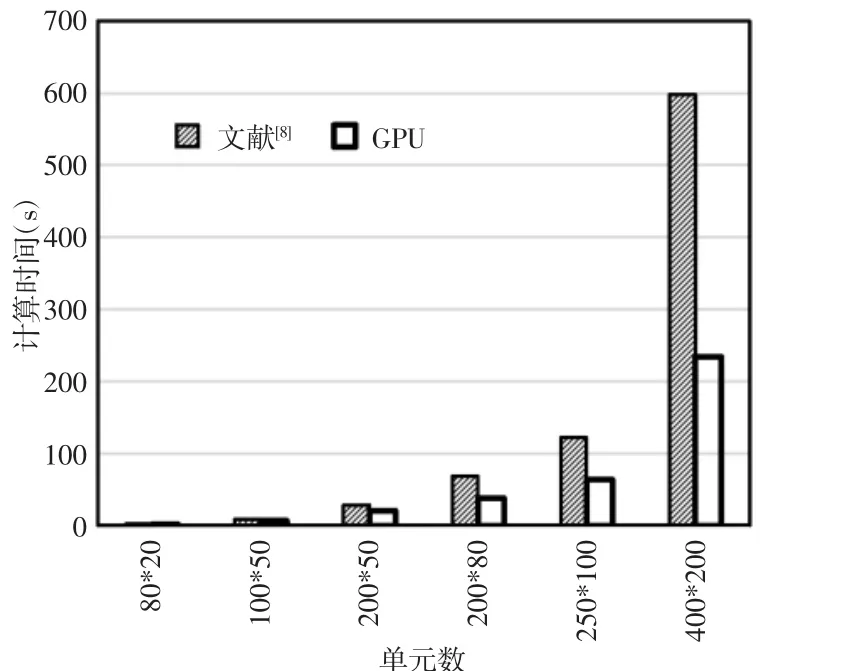
图7 简支梁算法效率比较柱状图Fig.7 Histogram of Algorithm Efficiency Comparison of Simply Supported Beam

4.2 悬臂梁

对悬臂梁拓扑优化问题，如图8所示。问题的设计域为160×100的矩形区域，左端边界固定，右下角加载方向向下的载荷F，材料需用体积为40%。

图8 悬臂梁问题简图Fig.8 Simplified Graph of Cantilever Beam

分别采用文献[10]和提出的GPU计算方法，柔度为优化目标，对结构进行拓扑优化计算，得到优化结果，如图9所示。可以看出，所述的GPU计算方法可以得到与文献[10]算法一致的优化结果，证明算法是有效的。

图9 悬臂梁优化结果对比Fig.9 Comparison of Optimization Results of Cantilever Beam

将算法与文献[10]的优化时间进行比较结果，如表4所示。可以看出，算法计算速度得到了提升，约是文献[10]计算速度的1.5倍，说明了算法的高效性。为了更直观的表达，给出了两算法计算时间的柱状图，如图10所示。

表4 悬臂梁算法效率比较Tab.4 Algorithm Efficiency Comparison of Cantilever Beam

图10 悬臂梁算法效率比较柱状图Fig.10 Histogram of Algorithm Efficiency Comparison of Cantilever Beam

5 结论

研究分析了基于SIMP法的二维结构拓扑优化方法，利用GPU并行计算对算法进行了改进，通过算例分析，得到了以下结论：（1）通过对二维结构化网格有限元分析过程的研究，提出了并行化有限元分析的计算方法，通过等效节点刚度的有限元分析法，加速了结构刚度矩阵的计算过程，相比现有的计算方法，计算速度得到了很大提升；（2）对二维结构拓扑优化计算过程进行了GPU层面的实现，并通过算例证实了方法的有效性，得到了比较理想的结构优化结果；（3）将所述的计算方法与文献[10]的计算方法进行了效率的比较，证明了GPU计算方法在解决拓扑优化问题的高效性。