线性回归分析在液体火箭推进剂温度预测中的应用

李大鹏，朱平平，陈士强，潘 辉，李若全

线性回归分析在液体火箭推进剂温度预测中的应用

李大鹏，朱平平，陈士强，潘 辉，李若全

（北京宇航系统工程研究所，北京，100076）

为研究液体火箭推进剂温度贴壁式测量替代插入式测量方法，消除推进剂插入式测温方式的隐患，基于一维稳态平板壁面传热学原理，建立理论数学模型，将火箭推进剂液体与壁面、环境大气三者之间换热关系的二元方程问题简化为一元方程问题，采用最小二乘法线性拟合，得出依靠壁面温度拟合推进剂温度的线性关联式。回归分析及实例验证了模型的正确性，并讨论了环境温度与壁面温度偏差等因素对测量精度的影响。结果表明：稳态换热条件下，利用壁温线性拟合推算推进剂温度方法可行，精度满足要求。

液体火箭推进剂；线性回归；最小二乘法；壁面温度

0 引 言

常规液体推进剂的温度作为运载火箭发射诸元之一，对火箭飞行工况、入轨精度有较大影响，准确测量推进剂射前温度，也是确保安全余量、贮箱气枕等技术指标满足发射要求的前提[1]。现行各型号运载火箭常规推进剂温度测量通常采用贮箱底部插入式铂电阻温度传感器实现，这种插入式测温方法具有插入较深、受贮箱外部环境影响小、测量精度高等优点，但这种测量方法需要在贮箱底部开孔安装温度传感器，会对加注后贮箱密封带来不利因素，存在贮箱推进剂泄漏的隐患。

目前推进剂温度监测通常同时采用“预测法”和“实测法”两种方法，其中推进剂发射温度预测法是由初始加注温度根据“平均环境温度”和时间变化量计算，称为“平均温度法”。万文明[8]等认为长时间的环境温度误差会对发射温度计算结果带来影响，因此提出改进的“积分法”，提高了推进剂发射预估温度计算精度，但改进后的发射温度预估方法精度依然会受实时环境温度、风速变化等方面因素影响，目前各型火箭仍保留“实测法”，将测试数据积累并作为依据对“预测法”模型不断修正优化。

本文基于传热机理，通过建立理论数学模型，利用运载火箭测量数据，开展了依靠壁面温度拟合推进剂温度的研究。

1 壁面温度热传递机理

1.1 推进剂温度测试系统

为研究贮箱壁面温度与推进剂温度之间的关系，在原有测试系统基础上增加了贴壁式测量，测试系统如图1所示。

图1 推进剂温度测试系统示意

由图1可知：推进剂测温插入式传感器和贴壁式传感器处于底部同一高度位置，两者均采用铂电阻传感器，其测量介质温度的方法是：在一定温度范围内，通过测定敏感元件的电阻-温度特性，再按照温度递增的顺序，用表格或曲线的形式制成分度表，根据测量的电阻值，查询分度表获取所测介质温度。该系统通过地面电缆和测试设备获取电阻值，并根据电阻-温度函数关系，得出实测温度。

1.2 推进剂与壁面温度关联性

实测过程中发现，在环境温度基本稳定的条件下，壁侧温度与推进剂温度通常存在恒定的偏差。图2给出了从历次试验中抽取的一组实测数据，截取了环境温度在20～26 ℃范围变化时某运载型号射前部分时段推进剂温度与贮箱壁面温度测量结果。根据历次实测数据结果的恒定偏差推测，长时间停放后贮箱推进剂温度与环境温度换热可能达到稳态平衡，两者存在一定的依存关系。为进一步验证推测，以某贮箱为例开展仿真计算，当推进剂温度和壁面初始温度一定时，选取外界环境温度为0 ℃、10 ℃时，分别获得了某燃料箱壁面温度与推进剂温度随时间的变化关系，仿真结果如图3所示（实测数据归一化处理）。

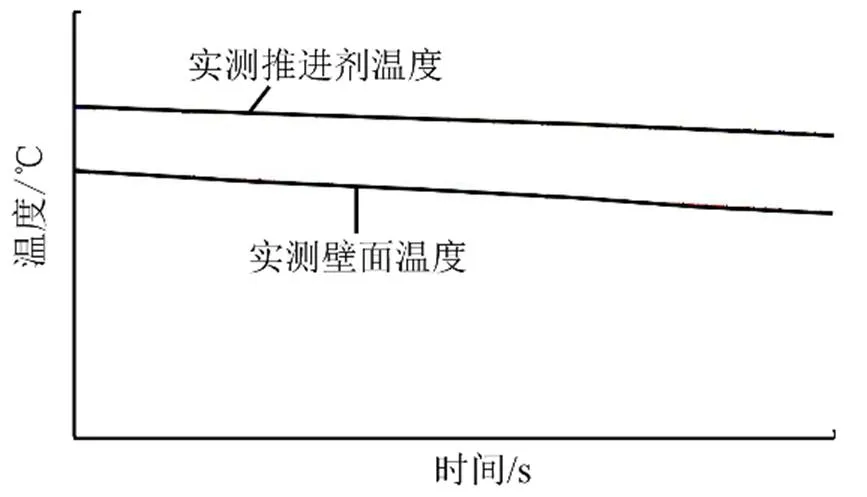
图2 推进剂与贮箱壁面温度实测数据对比

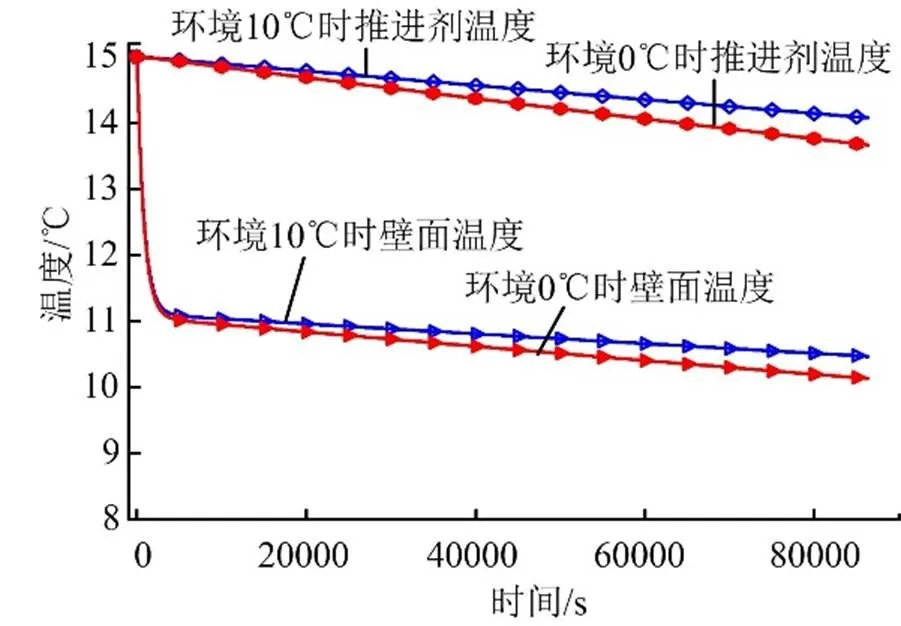
图3 推进剂与贮箱壁面温度仿真结果对比

由图2、图3可以看出，贮箱壁面温度与实测推进剂温度存在一定的固有偏差，外界环境温度与推进剂温度温差较大时，壁面温度与推进剂实际温度偏差也大，若能找到稳态换热状态下壁面温度与环境温度偏差影响因子，则可以得到对应时段以壁面温度替代推进剂实测温度的有效方法。

1.3 传热理论数学模型

根据上述推测，为进一步分析推进剂温度与壁面温度的关联性机理，将基于壁面温度测点数据、环境温度及推进剂温度数据探讨推进剂温度变化与环境及壁面温度的关系。

箭体停放达到一定时间后，环境与箭体壁面及推进剂换热逐渐达到稳态，此时可以利用环境温度和其他变量建立推进剂温度的预测公式，在稳态导热情况下，尽管时间逐渐发生变化，但温度场始终不变。对于平壁两表面来说，温度缓慢变化的情况下，平壁导热过程从性质上讲可以认为是一维稳态导热，图4为通过平壁模型的传热过程示意，火箭贮箱内推进剂通过箱壁与环境换热可以通过该模型描述[9]。

图4 平壁模型传热过程示意

常规推进剂加注一般在发射前1～3天进行，通常经过24 h以上的停放，可近似认为贮箱与环境处于热平衡状态，此时两侧流体与壁面的对流传热量均等于壁面之间的传热量，即：

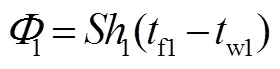
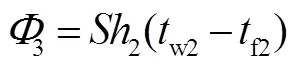
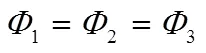
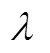
进一步整理可得：

式中为比例系数。

根据上述推导可知，内侧流体与外壁面的温度差正比于外壁面与外流体温度之差，两者为线性关系，影响因素包括对流换热系数和壁面物性参数。壁面物性参数在0～20 ℃变化很小，可近似认为是常数，而对流换热系数受对流换热壁面流速影响明显，尤其是外壁面与环境的风速。因此，对应不同环境条件，比例系数会有所差异。

2 拟合步骤和应用实例

2.1 线性回归分析

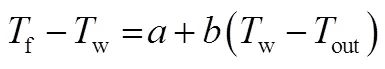
b）用最小二乘法进行线性拟合[11~14]。使用线性回归分析regress( )函数，调用格式为

[,bint,r,rint,stats]=regress(,)

表1 Matlab拟合出的参数值

Tab.1 Fitting Parameter Dependent on Matlab

项目检验回归模型的统计量 参数代号FP 数值0.777973.67764.5891×10-50.0184

图5 散点及线性回归特性曲线

图6 残差计算结果

2.2 验证实例

拟合回归测试结果验证了模型的正确性，残差分析结果表明回归模型具有较好的精度，可以满足未来数据的预测正确性和精度。为进一步验证拟合模型预测精度，选取第18次实测结果进行验证，验证结果如图7所示，拟合结果与实测偏差为0.17 ℃，满足精度要求，模型正确性得到验证。

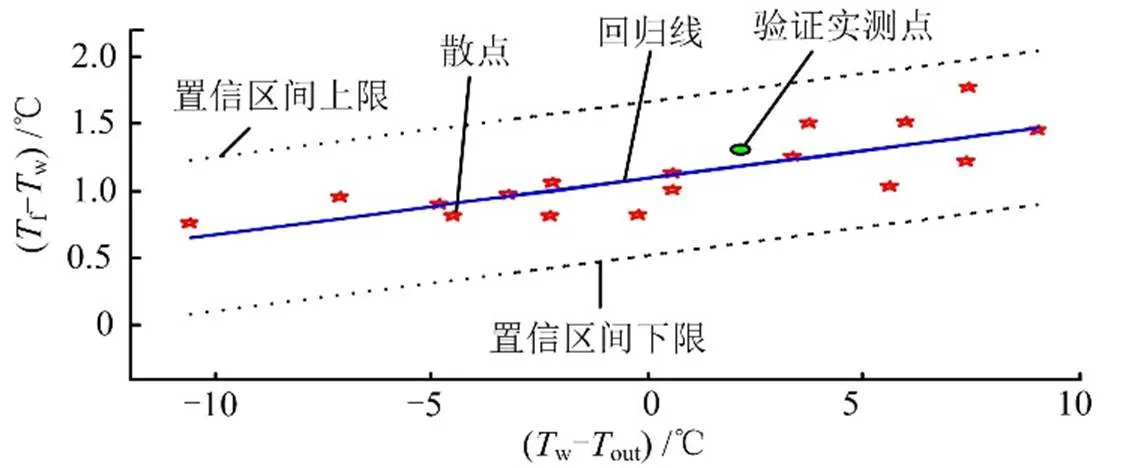
图7 实测结果对比

2.3 偏差影响因素分析

回归模型确定后，环境温度和壁面温度则是影响模型精度的两个重要因素，影响程度分析具体如下：

a）环境温度测量偏差影响。

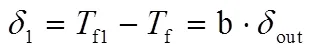
b）壁面温度测量偏差影响。

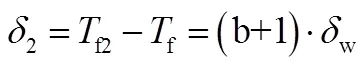
c）其它影响因素。

除壁面温度与推进剂温度固有偏差外，贴壁式测温自身测量精度也很重要，其影响因素较多，由于壁温传感器敏感面与被测物体表面贴合，传感器敏感的温度与被测物体表面基本相同，为了减少外界环境的影响，一般会对壁温传感器采取隔热处理；另一方面，表面黏贴质量影响较大，外界环境温度通过传感器金属外壳传递到敏感面处，表面黏贴的稳定性和可靠性对测量结果的准确性具有较大影响。

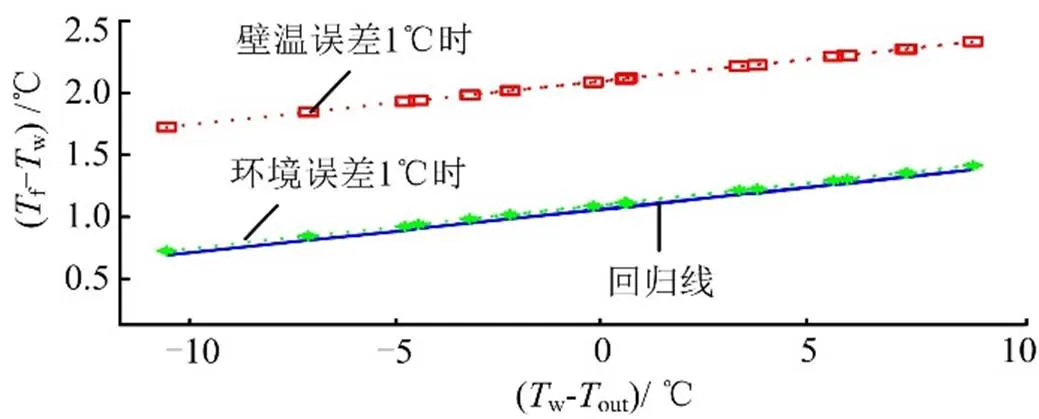
图8 测量偏差影响特性

从图8中可以看出，温度拟合误差受壁温的影响程度更大。其它方面，壁温传感器表面黏贴质量也是重要影响因素之一，应尽可能提高壁面温度测量精度减少测量误差。

3 结束语

本文利用实测温度数据样本，建立传热理论数学模型，将火箭推进剂液体温度与壁面温度、环境大气温度三者之间换热关系的二元方程问题简化为一元方程问题，采用最小二乘法拟合，开展基于壁温测量的液体火箭推进剂温度预测模型研究。研究表明：a）壁温预测的理论数学模型和回归分析模型正确、线性回归方程拟合程度较好、回归方程显著、实例验证结果精度满足要求；b）相比环境温度偏差，壁面温度偏差影响程度更大，应尽可能提高壁面温度测量精度，减少测量误差；c）与“平均温度法”和“积分法”相比，线性回归分析方法基于当前实测数据，测量精度不受火箭停放时间影响，更实用有效。

[1] 刘庆才, 周彦煌, 刘东尧. 130火箭推进剂非稳态温度场特性数值研究 [J].弹箭与制导学报, 2002, 22(2): 64-67.

Liu Qingcai, Zhou Yanhuang, Liu Dongyao. Numerical research on transient temperature field characteristics of 130 rocket propellant journal of projectiles[J]. Rockets, Missiles and Guidance, 2002, 22(2): 64-67.

[2] Habib M A, et al. Velocity char-acteristics of turbulent natural convection in symmetrically and asymmetrically heated vertical channels[J]. Experimental Thermal and Fluid Science, 2002, 26: 77-87.

[3] Wardana N G, et al. Structure of turbulent two-dimensional channel flow with strongly heated wall[J]. Experiments in Fluids, 1992, 13: 17-25.

[4] 马良栋, 等. 具有截面自然对流通道内湍流换热的直接数值模拟[J]. 西安交通大学学报, 2007, 41(3): 367-371.

Ma Liangdong, et al. Direct numerical simulation of turbtdent flow and heat transfer in square duct with steady natural convection in cross section[J]. Journal of Xi' an Jiaotong University, 2007, 41(3): 367-371.

[5] Hattori Y, et al. Turbulence characteristics of natural-convection boundary layer in air along a vertical plate heated at high temperature[J]. International Journal of Heat and Fluid Flow, 2006, 27: 445-455.

[6] 闫理贵, 傅松. 竖直加热平板对流边界层的数值模拟[J]. 山东大学学报, 2009, 3(6): 143-146.

Yan Ligui, Fu Song. Numerical simulation of the convection boundary layer in a.ir along a vertical heated plate[J]. Journal of Shandong University, 2009, 3(6): 143-146.

[7] 李珍, 等. 竖壁自然对流的数值模拟[J]. 黑龙江科技院学报, 2008, 18(1): 58-60.

Li Zhen, et al. Numerical simulation of natural convection along a vertical wall[J]. Journal of Heilongjiang Institute of Science&Technology, 2008, 18(1): 58-60.

[8] 万文明, 陈根仪. 液体火箭推进剂温度计算方法优化研究[J]. 载人航天2006(4): 49-52.

Wan Wenming, Chen Genyi. Research on optimization of calculation method for propellant temperature in liquid rocket[J]. Manned Spaceflight 2006(4): 49-52 .

[9] 杨世铭, 陶文铨. 传热学(第四版)[M]. 北京: 高等教育出版社, 2006.

Yang Shiming, Tao Wenquan. Heat transfer(4th edition)[M]. Beijing: Higher Education Press, 2006.

[10] 黄育红, 等. 基于MATLAB 的二元线性回归在小孔流速实验中的应用[J]. 大学物理实验, 2016, 29(1): 94-97.

Huang Yuhong, et al. The application of binary linear regression in the experiment of keyhole flow velocity based on MATLAB[J]. Physical Experiment College, 2016, 29(1): 94-97.

[11] 汪奇生, 等. 总体最小二乘线性回归统一模型及解算[J]. 工程勘察, 2014(4): 87-90.

Wang Qisheng, et al. The unified model and algorithm of total least squares linear regression[J]. Geotecltnical Investigation & Surveying, 2014(4): 87-90.

[12] 许超钤, 等. 基于整体最小二乘的参数估计新方法及精度评定[J]. 测绘通报, 2011(10): 1-4.

Xu Chaoqian, et al. New method of parameters estimation and accuracy evaluation based on TLS[J]. Bulletin of Surveying and Mapping, 2011 (10): 1-4.

[13] 鲁铁定, 陶本藻, 周世健. 基于整体最小二乘法的线性回归建模和解法[J]. 武汉大学学报(信息科学版), 2008, 33(5): 504-507.

Lu Tieding, Tao Benzao, Zhou Shijian. Modeling and algorithm of linear regression based on total least squares[J]. Geomatics and Information Science of Wuhan University (Information Science Edition), 2008, 33(5): 504-507.

[14] 陈岚峰, 等. 基于MATLAB的最小二乘曲线拟合仿真研究[J]. 沈阳师范大学学报(自然科学版), 2014, 32(1): 75-79.

Chen Lanfeng, et al. MATLAB simulation of curve fitting based onleast squares[J]. Journal of Shenyang Normal University (Natural Science Edition), 2014, 32(1): 75-79.

Application of Linear Regression Analysis on Liquid Rocket Propellant Temperature Predication

Li Da-peng, Zhu Ping-ping, Chen Shi-qiang, Pan Hui, Li Ruo-quan

(Beijing Institute of Astronautical Systems Engineering, Beijing, 100076)

Adherent measurement of liquid rocket propellant temperature instead of insert measurement is investigated to avoid hazards. The theoretical model is established base on one-dimensional steady-state principle of flat wall heat transfer. The heat transfer relationships among propellant, wall, and enviroment,which are equations with two variables are smplified to a equation with one variable. The linear relation between propellant temperature and wall is derived by linear fitting using least square method. Correctness and effectiveness of the model are verified by living examples and regression analysis by which the influence of measurement error of enviroment temperature and wall temperature on result are discussed. The results show that the propellant temperature can be predicted by linear fitting using wall tempreature at steaty-state heat transfer condition and the precision meet the requirements.

liquid rocket propellant; linear regression; least square fitting; wall temperature

V434

A

1004-7182(2020)01-0043-05

10.7654/j.issn.1004-7182.20200108

2019-08-23；

2019-11-19

李大鹏（1971-），男，高级工程师，主要研究方向为液体火箭动力系统总体设计。

朱平平（1989-），男，工程师，主要研究方向为液体火箭动力系统总体设计。

陈士强（1987-），男，博士，高级工程师，主要研究方向为液体火箭动力系统总体设计。

潘 辉（1984-），女，高级工程师，主要研究方向为液体火箭动力系统总体设计。

李若全（1970-），男，高级工程师，主要研究方向为液体火箭仪器电缆设计。