地面供配气系统中孔板节流特性分析

王营军，陈 山，全承哲，白 华

地面供配气系统中孔板节流特性分析

王营军，陈 山，全承哲，白 华

（北京航天发射技术研究所，北京，100076）

孔板节流是简单可靠、应用广泛的地面供配气系统节流方式。分析了孔板节流过程中的流动特性。声速前充气阶段为系统中阀门开启至稳定声速流动阶段，持续时间较短。当孔板上游压力达到一定值后，充气过程存在声速充气现象，在工质确定的前提下，该过程的充气流量只和孔径大小成正比，该阶段为声速充气阶段。随着充气量的增加，背压提升导致孔板前后的压差逐渐减小，声速后充气阶段质量流量随着前后压差的缩小而逐渐减小。对地面供配气系统中孔板节流方案的设计有工程指导意义。

供配气系统；孔板节流；数值仿真；充气过程

0 引 言

孔板节流常被用于流体管路输送系统中，尽管在工业生产中已被广泛应用[1~3]，但是其设计和制作所需的各个参数尚处于靠经验取值的阶段。在孔板的流量计算中，冯建生[4]通过对孔板流量计结构、测量原理、公式来源的分析，找到合理准确的公式，解决工作中遇到的问题，方便了工程的实际应用。

关于孔板上下游的气流脉动问题也有研究[5,6]，白文杰[7]在高压管路中单独使用孔板来消减脉动效果，通过添加适当尺寸的孔板起到一定的脉动消减效果，且此效果随孔径比减小而逐渐增强，此外需要考虑孔板的阻力作用及后续工艺条件等因素。吴石[8]研究了蝶阀、闸阀和球阀在开度减小的过程中流场的变化和噪声问题，流体在蝶阀背面、球阀阀门内外分别形成两个方向相反的漩涡，闸阀的漩涡出现在挡板与管道的避角处，并且漩涡在阀门下游逐渐消失，并通过试验表明阀门下游的流噪声大于阀门上游的流噪声，涡声是阀门噪声的主要来源。

孔板下游回流区大小直接影响压力传感器的安装，具体的影响区域可以通过数值仿真进行分析[9,10]。文献[11]运用Fluent软件分析了管道流动中孔板消减脉动作用，并采用标准的双方程湍流模型较为准确地计算了管道系统的流场特性。艾万政[12]研究表明在雷诺数和孔板厚度不变的情况下，回流区长度随孔径比的减小而增大；在雷诺数和孔板比不变的情况下，回流区长度随孔板厚度的增加而减小；当雷诺数增加至一定值后，回流区长度几乎不随雷诺数的变化而变化。

综上所述，关于孔板节流的相关研究主要集中在孔板的尺寸和上下游的脉动上，针对孔板充气的整个过程和上下游流场的研究较少。本文主要对采用孔板节流的供配气系统进行了研究，并验证不同的孔板在充气过程中的节流特性，以此为基础详细分析了充气过程中孔板上下游流场特性的差异。

1 供配气系统数值模型介绍

在供配气系统中如果使用质量流量控制器进行充气，根据气瓶的容积提前计算出要充气的质量，然后分阶段完成充气。刚开始设定较大的流量充气一段时间，在即将结束充气时，改用小流量进行充气，导致在充气即将结束时的余速较大，严重影响增压后效问题。

由于地面供配气系统在空间布局上需要考虑结构紧凑，而质量流量控制器占用空间大，还需要定期进行校核。孔板相比于质量流量控制器的优点包括：方便拆卸和校核、便于维护。因此选择孔板来代替质量控制器控制流量完成充气。

图1为带有孔板的管路系统AMESim模型，在充气过程中分两个阶段进行充气，并对气瓶的瞬时压力进行监测并加以判断，第1次判断是为了控制对气瓶的快速充气和缓慢充气，并在充气过程中对测量值进行第2次判断，根据任务要求来确定充气是否完成。

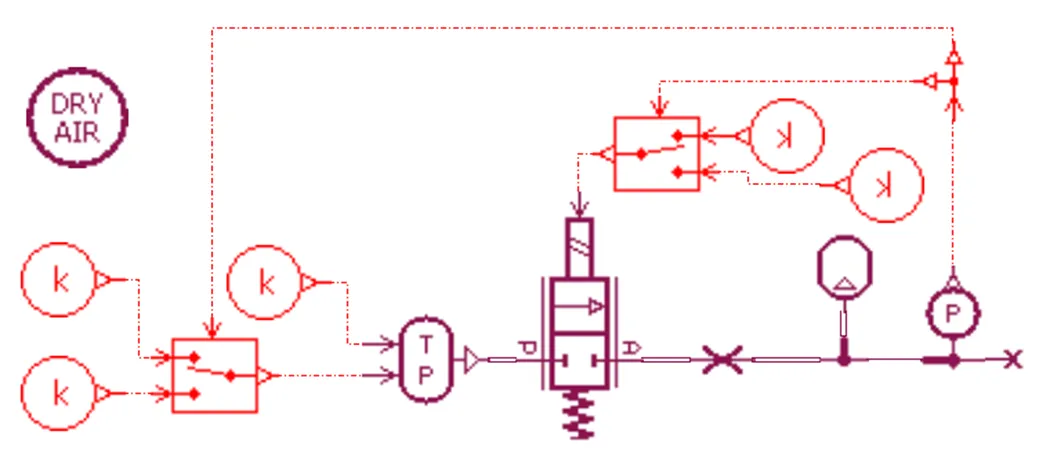
图1 供配气系统AMESim模型示意图

为了验证系统加装节流孔板后的可靠性，对该地面供气系统进行了试验，按照程序分别监测了快速充气和缓慢充气过程。在节流孔板几何一定的条件下，对产品进行多次测量，其中快速充气过程持续了 31~ 35 s，缓慢充气过程持续了58~62 s。使用图1的计算模型，发现快速充气和缓慢充气过程分别为34 s和 60 s，计算结果落在了试验测量的区间内，该计算模型可以较好地模拟带有节流孔板的管路充气系统。

2 孔板节流特性

2.1 充气过程压力变化区间分析

在整个充气过程中流场参数的变化主要受到前后压差的影响。随着充气量的增加，管路中压差变小，管路中流量逐渐减小。图2为整个充气过程中气源压力和容腔压力及其流量的变化曲线，设置一定的阈值将整个充气过程分为两个阶段进行充气。从流量变化曲线可以发现，在开始充气100 ms的时间内，管路中流量迅速增加，该阶段持续时间极短，由于该供配气系统管路的空间较小，流体很快充满整个系统，对整个充气过程影响较小，所以在下面分析中可以忽略该阶段。然后进入稳定的充气阶段，该阶段容腔内的压力线性增加，流量保持不变。由压力变化曲线可以判断，孔板前后压差的比值小于临界压力比0.528，所以管路中孔板部分一直处于声速状态，在该阶段容腔中的压力和流量呈线性增加，而且流过孔板的流量只和孔板的大小有关。在容腔中的质量接近目标值80%时，通过调节孔板前减压阀将充气气源的压力减小，根据调整后的气源压力和容腔压力可以判断，在后期充气过程中，管路中的空气处于亚声速状态，随着容腔中压力逐渐增加，管路中压差逐渐减小，流量也减小。当容腔中的压力达到目标值后，关闭管路中电磁阀，此时，由于整个供配气管路中压力不均匀，导致流量出现了一定的波动。整个充气过程总流量和持续的时间满足要求。

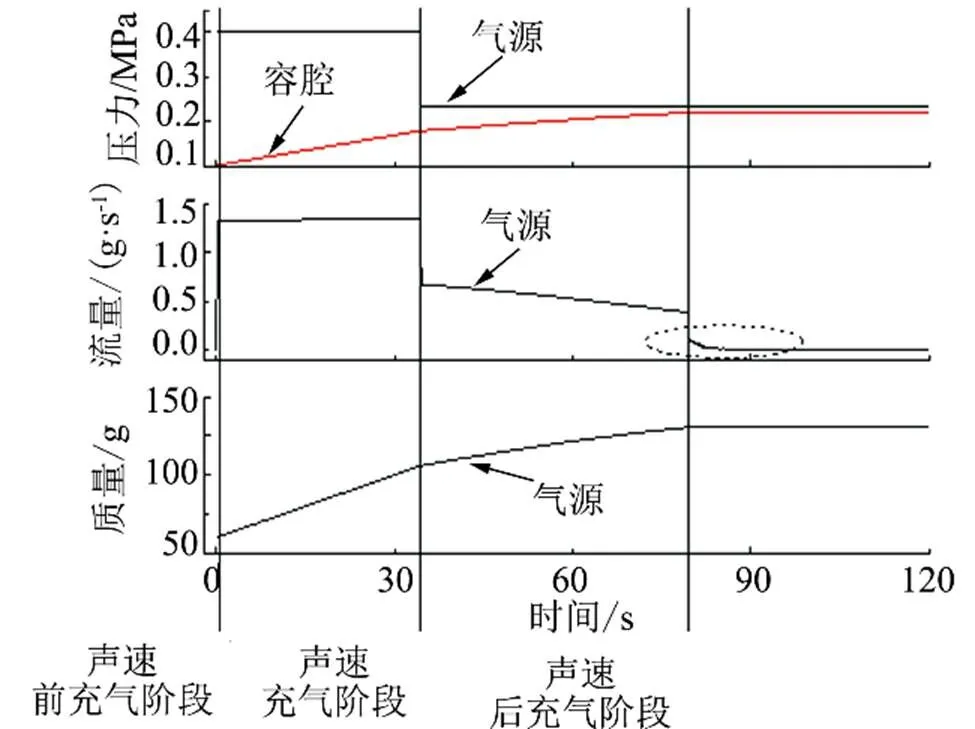
图2 充气过程静压及流量变化曲线

2.2 不同孔径的孔板对节流的影响

由上述分析可知，声速充气阶段空气的速度达到最大值，通过的质量流量最大，该过程持续时间的长短对整个充气过程有重要影响。因此，在相同的控制策略下，对不同孔径的孔板的充气过程做了对比。图3为3个孔径分别为1.2 mm、1.6 mm和2.0 mm孔板的充气过程变化曲线。从图3中可以发现，在声速充气阶段，随着孔径的增加，通过孔板的流量也增加，容腔中的压力提升的最快。当容腔中的压力达到同一阈值时，进入亚声速充气阶段，在相同的压差驱动下，大孔径的孔板流量最大，首先完成充气。所以，孔板尺寸不仅影响声速充气阶段，而且影响亚声速充气阶段。

图3 不同孔径的节流效应

2.3 不同阈值对节流的影响

不同的控制策略也会对充气过程产生影响，在声速充气阶段向亚声速充气阶段转换时，设定合理的阈值可以改变不同阶段的充气时间，从而影响整个充气过程。为了考虑不同阈值对节流的影响，图4对比了 3个阈值分别为1.5 kPa、1.8 kPa和2.1 kPa的充气过程，这3种阈值和气源压力的比值都小于0.528，所以，在转换之前都是声速充气，在孔径相同的前提下，进入容腔的空气质量和时间成正比。由于速度达到最大值，该阶段持续时间越长，可以较早的完成充气过程。

声速充气过程持续时间越长容腔充气的时间越短，图5对比了整个过程都是声速充气和分阶段充气时容腔流量的变化曲线。从图5中可以发现，虽然声速充气可以很快充满容腔，但在电磁阀关闭后，管路系统中流量的波动较大，如图5中圆圈所示。这是由于声速充气完成后管路中的压差较大，而且整个管路中气流余速较大，形成了流量曲线的振荡，而且造成管路系统压力振荡和气动噪声。

图4 不同阈值的节流效应

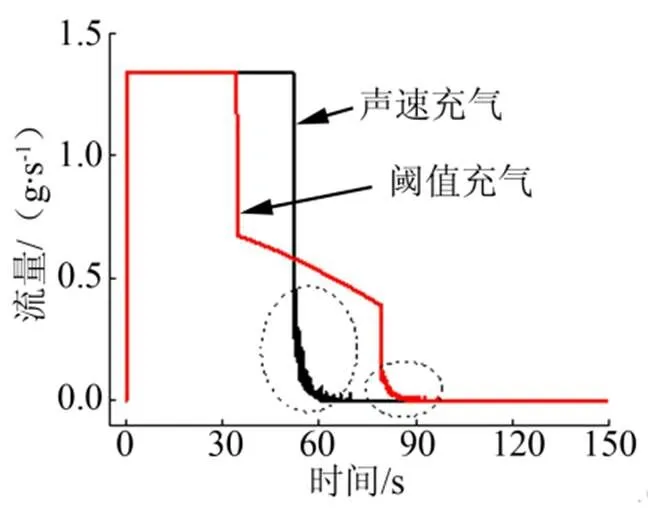
图5 不同充气速度下流量变化

3 孔板节流的流场分析

为进一步分析在充气过程中孔板模型流场的变化，对孔板节流进行几何建模和数值仿真计算。由于该结构是轴对称结构，在建模时采用二维模型，其中管路直径为6 mm，上下游分别计算10倍和15倍的管路直径，孔板的厚度为0.5 mm，整个流场都采用结构型网格划分，在孔板附近需要加密网格，最后网格数量为53万。使用Fluent软件进行计算，采用轴对称边界来减少网格的数量和计算的时间，将AMESim中计算得出的孔板前后的压力变化作为计算的边界，使用UDF来编译进出口静压随时间的变化曲线，湍流模型采用标准的模型，时间步长为0.2 s。

图6为不同充气阶段中间时刻的压力和速度变化云图，上下游分析区域分别为1倍管径和4倍管径。在快速充气阶段孔板上游的压力明显大于下游压力分布，较大的压差导致在孔板下游大约1倍管径处存在较大的压力梯度，分析对应位置的速度云图发现了激波现象，激波严重阻碍了气流的运输，并且在上下壁面存在强烈的射流，其下游影响范围大约在8倍管径。而在缓慢充气阶段，上下游压差较小，在孔板下游存在明显的射流特性，射流区域内的流体速度不超过250 m/s，射流的影响范围大约在5倍管径。所以在孔板下游安装传感器时，应该充分考虑孔板节流带来的非均匀流场的影响。

图6 不同阈值的节流效应

从图6可以发现，管路中轴线上的流场变化较为剧烈。图7对不同充气阶段中间时刻中轴线上的压力和速度进行量化对比。

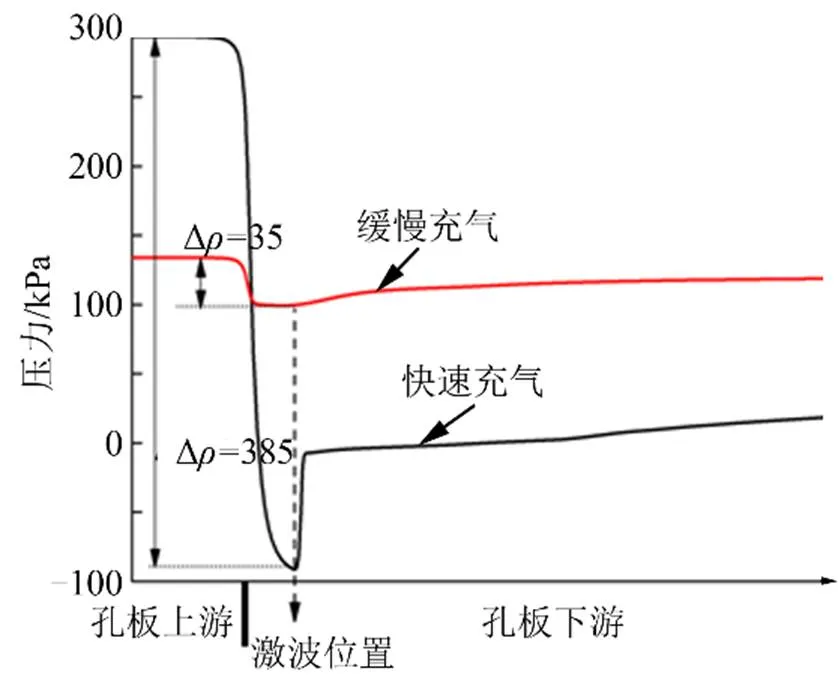
a）压力变化

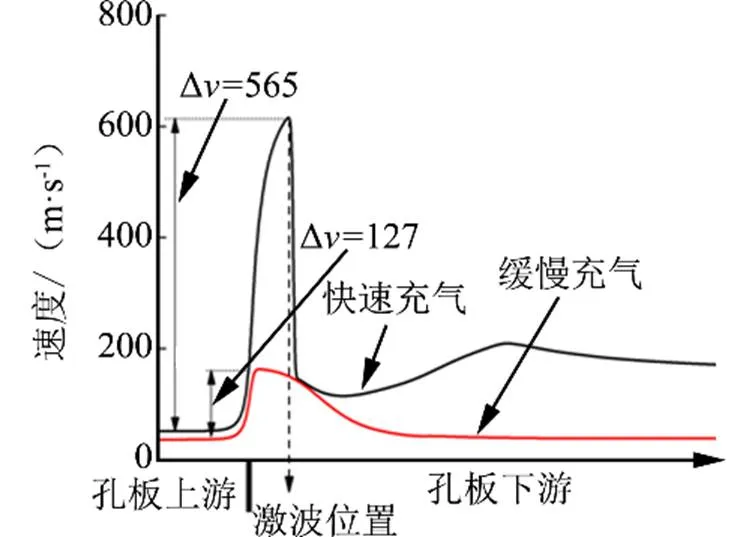
b）速度变化

续图7

从图7中可以看出，在快速充气阶段气流通过孔板压力的最大值为385 kPa，该压力值远大于缓慢充气阶段对应的35 kPa，同时，快速充气阶段速度的最大值为565 m/s，也大于缓慢充气阶段对应的127 m/s。在图6中相对应的位置处存在较大的梯度，在激波前速度达到最大值，气流在通过激波后压力突然升高，速度下降。快速充气的流场变化明显大于缓慢充气时的流场特性。

图8为整个充气过程中沿中轴线的压力和速度变化时空图。在快速充气阶段，孔板下游大约1倍管径距离处一直存在激波现象，其堵塞响应导致流体在激波前后压力突然升高，速度下降。在缓慢充气阶段，随着背压的增加，射流影响长度逐渐减小。孔板后的背压逐渐接近任务要求，孔板前后的压差达到最小值，气流产生的余速也较小。当背压达到目标值后，关闭进口电磁阀，完成供配气要求。

图8 不同充气阶段中间时刻沿中轴线压力和速度时空图

4 结 论

本文研究了地面供配气系统中孔板节流的流场特性，首先利用AMESim软件对整个供配气系统进行了仿真，发现使用孔板来实现供配气更有优势，对比了不同孔径的孔板和阈值对充气过程的影响，并使用Fluent软件来模拟充气过程中不同阶段的流场特性，主要结论如下：

a）使用孔板节流来代替质量流量控制器更有优势。由于孔板制造简单、便于拆卸和维护方便在管路系统中被广泛使用。在孔板节流后期，背压的逐渐提高导致流速缓慢降低，这样更有利于实现缓慢充气，减少增加后效问题。

b）对比了不同孔径和阈值对充气过程的影响。在声速充气过程中，充气的流量只和孔径的大小有关，而较大的阈值可以延长声速充气的持续时间。在对充气时间有要求时，就需要选择大小合适的孔板和合理的阈值来优化充气控制策略。

c）数值计算结果表明，在声速充气阶段孔板下游存在激波，气体通过激波后，速度突然降低，压力突然升高。在亚声速充气阶段，孔板下游存在明显的射流现象。所以在孔板下游安装传感器时，应该适当考虑距离孔板的流向距离，减小射流对数据采集的影响。

[1] 董未来. 煤矿瓦斯抽放计量中常见的问题与分析[J]. 煤矿现代化, 2009(6): 79-80.

Dong Weilai. Coal mine gas drainage measurement and analysis of commom problems[J]. Gas Mine Modernization, 2009(6): 79-80.

[2] 尹广增. 孔板流量计计量误差现场因素分析[J]. 石油工业技术监督, 2009(6): 15-17.

Yin Guangzen. An analysis of factors about measuring errors of orifice flowmeters[J]. Tecchnology Supervision in Petroleum Industry, 2009(6): 15-17.

[3] 梁国伟. 差压式流量计测量不确定度的经验估计[J]. 计量技术, 2000(5):23-25.

Liang Guowei. Empirical estimation of measurement uncertainty of differential pressure flowmeter[J]. Measurement Technique, 2000(5): 23-25.

[4] 冯建生. 孔板流量计测量原理及流量计算存在问题分析[J]. 煤矿安全, 2014, 45(10):218-221.

Feng Jiansheng. Measurement principle of orifice flowmeter and its calculation formula problem analysis[J]. Safety in Coal Mines, 2014,

45(10): 218-221.

[5] 宋辉辉, 等. 孔板消减气流脉动的数值模拟及实验研究[J]. 应用力学学报, 2011, 28(1): 39-43.

Song Huihui, et al. Numerical simulation and experimental research on orifice plate reducing gas pulsation[J]. Chinese Journal of Applied Mechanics, 2011, 28(1): 39-43.

[6] 鄢曙光, 祝振杰. 基于FLUENT的孔板消减气流脉动的数值模拟. [J]. 液压与气动, 2016(7): 77-82.

Yan Shuguang, Zhu Zhenjie. Numerical simulation of orifice plate reducing gas pulsation based on FLUENT[J]. Chinaese Hydraulic & Pneumatics, 2016(7): 77-82.

[7] 白文杰, 等. 孔板消减气流脉动的数值模拟[J]. 应用力学学报, 2013, 30(6): 828-832.

Bai Wenjie, et al. Numerical simulation of orifice plate reducing gas pulsation[J]. Chinese Journal of Applied Mechanics, 2013, 30(6): 828-832.

[8] 吴石, 张文平. 阀门流场的数值模拟及流噪声的实验研究[J]. 阀门, 2005(1): 7-10.

Wu Shi, Zhang Wenping. Investigated numerically on flow-field of valves and experimental study of valve-noise [J]. Valve, 2005(1): 7-10.

[9] 党锡淇, 陈守五. 往复式压缩机气流脉动与管道振动[M]. 西安: 西安交通大学出版, 1984.

Dang Xiqi, Chen Shouwu. Air flow pulsation and pipeline vibration of reciprocating compressor[M]. Xi'an: Xi'an Jiaotong University Press, 1984.

[10] 苏永生, 王恒杰. 应用CFD消除气流脉动[J]. 华东理工大学学报, 2006, 32(4): 480-483.

Su Yongsheng, Wang Hengjie. Using CFD in reducing airflow ripple[J]. Journal of East China University of Science and Technology (Natural Science Edition), 2006, 32(4): 480-483.

[11] 韩文龙, 韩省亮, 白长青. 往复式压缩机管道系统气流脉动的数值与实验研究[J]. 西安交通大学学报, 2013,47(5):1-6.

Han Wenlong, Han Shengliang, Bai Changqing. Numerical and experimantal research on gas pulsation in reciprocating compressor piping system[J]. Journal of Xi'an Jiaotong University, 2013, 47(5): 1-6.

[12] 艾万政, 周琦. 孔板后回流区长度数值模拟研究[J]. 水动力学研究与进展, 2011,26(6): 731-735.

Ai Wanzheng, Zhou Qi. Study on the length of the recirculation region behind the orifice plate based on numerical simulation[J]. Chinese Journal of Hydrodynamics, 2011, 26(6): 731-735.

Analysis of the Orifice Plate Throttling in Gas Supply and Distribution Ground System

Wang Ying-jun, Chen Shan, Quan Cheng-zhe, Bai Hua

(Beijing Institute of Space Launch Technology, Beijing, 100076)

The simple and reliable orifice plate throttling is widely used in gas supply and distribution ground system. The throttling characteristics of the orifice plate are analyzed. The duration from the valve opening to stable sonic flow lasts a little while before the sonic gas charging stage. When the pressure reaches a certain value at the upstream of the orifice plate, the gas charging becomes the sonic charging phenomenon, whose flow characteristics only is proportional to the size of the orifice aperture under the determination of the working substance. With the increase of charging amount, the gradually increasing back pressure results into the decreasing differential pressure of orifice plate. Accompanied by the gradually decreasing flow rate at stage after sonic charging. The design of orifice plate throttling scheme is useful for engineering application.

gas supply and distribution system; orifice plate throttling; numerical simulation; charging process

V421.7

A

1004-7182(2020)01-0094-0

10.7654/j.issn.1004-7182.20200117

2018-01-23；

2018-07-19

王营军（1988-），男，博士，工程师，主要研究方向为气体动力学。

陈 山（1983-），男，博士，工程师，主要研究方向为流体机械。

全承哲（1979-），男，工程师，主要研究方向为气动阀件。

白 华（1971-），女，工程师，主要研究方向为气动阀件。