基于滑模的运载器主动段俯仰通道姿控系统设计

石宝兰，韩 璐，李紫光，张广勇，化 金

基于滑模的运载器主动段俯仰通道姿控系统设计

石宝兰，韩 璐，李紫光，张广勇，化 金

（北京宇航系统工程研究所，北京，100076）

与传统比例-积分-微分（PID）控制方法相比，滑模控制（SMC）方法可以比较容易地将不确定性纳入控制器设计中，从而增强系统的鲁棒性。探索了SMC技术在运载器主动段姿态控制中的工程应用，首先通过分析基于趋近律的SMC系统，提出了降低不连续切换项系数的需求，然后研究了基于干扰上界的SMC方法。三通道小偏差仿真结果验证了两种方法的控制效果，表明第2种控制器的鲁棒性更好，稳态误差小，同时发动机喷管摆角需求较小。

姿态控制；滑模控制；不确定性；干扰上界

0 引 言

目前运载器的姿控系统设计以传统的比例-积分-微分（PID）控制器设计方法为主，该方法在控制领域得到了最广泛的应用。然而，该方法也存在一些局限性：比较耗时，工作量较大；对控制器参数的调整依赖设计师的经验；飞行包络的改变可能会导致设计方案的调整。

滑模控制（Sliding Mode Control，SMC）是现代控制方法中新设计思想的代表之一。对于飞行包络、环境参数、运载器自身参数等的变化，SMC方法可以比较容易地纳入系统的控制器设计中，从而增强系统的鲁棒性。此外，与其它鲁棒设计方法相比，SMC还具有响应快速、无需系统在线辨识、设计过程和物理实现都比较简单等优点。在飞行器控制领域，许多学者致力于研究SMC在可重复使用运载器、现代战斗机、无人飞行器和柔性空间飞行器等不确定性较强系统的飞行控制中的应用，取得了大量成果。不过SMC技术应用于工程时仍需解决一些问题，最主要的问题是抖振。Slotine[1,2]提出的“边界层”和“准滑动模态”概念为SMC工程降抖开辟了道路。

本文旨在探索SMC技术在运载器主动段姿态控制中的工程应用，以期为SMC技术的工程应用做一些有益积累。首先从直观有效的基于趋近律的SMC控制器的设计入手，通过仿真分析提出了降低不连续切换项系数的需求；为此，根据工程经验估算干扰上界，研究了基于干扰上界的SMC控制器设计，并通过三自由度小偏差仿真验证了其控制效果。

1 俯仰通道姿态运动模型

1.1 俯仰通道小扰动姿态运动模型

姿态控制研究的是运载器绕质心运动，可分解为俯仰、偏航和滚转3个通道。对于轴对称运载器，主动段各通道间的耦合很小，可按通道独立进行姿态控制系统设计。忽略主发动机喷管摆动产生的惯性力和惯性力矩中与摆动角加速度有关的项，在箭体坐标系下建立俯仰通道绕质心动力学方程[3]。飞行过程中，扰动作用与已建模作用相比量级较小，扰动弹道在未扰动弹道附近摄动。因此可忽略动力学方程中的高阶项，对描述实际姿态运动的非线性方程进行线性化。对于主要在射面内运动的运载器，采用小扰动法得到俯仰通道线性化运动方程[4]：

1.2 模型不确定性

模型式（2）未考虑干扰，实际上存在不确定性，包括外部干扰和参数摄动等。

1.2.1 干扰因素

运载器主动段，影响飞行状态的外界干扰因素包括风干扰、结构干扰以及级间分离干扰等，其中风干扰和结构干扰为主要因素。风干扰造成附加风攻角和风侧滑角，主要考虑平稳风和切变风两种情况。结构干扰是生产过程中的工艺误差和安装误差造成的，主要包括箭体轴线偏斜、质心偏移、发动机安装误差产生的推力线横移和推力线偏斜、空气舵安装误差等，通过与气动力或发动机推力耦合产生干扰力和干扰力矩。

本文考虑的俯仰通道干扰力矩包含4项：a）箭体质心随机横移、质心常值横移和发动机推力线横移引起的干扰力矩；b）发动机推力线偏斜引起的干扰力矩；c）各端面初始对接误差产生的攻角引起的干扰力矩；d）空气舵安装误差产生的攻角引起的干扰力矩。

1.2.2 偏差量

总体、气动和大气等参数无法精确获得，设计使用的数值与运载器实际飞行时的数值相比存在一定偏差，设计时采用参数偏差带对这部分不确定性进行包络[6]。本文考虑的参数偏差如下：

a）总体参数偏差：质心轴向偏差，质心随机横移，转动惯量偏差，发动机推力线偏斜，发动机推力线横移，端面初始对接误差和空气舵安装误差；

b）气动参数偏差：阻力系数偏差，升力系数导数偏差，滚转力矩系数偏差和其它气动参数偏差。

2 基于趋近律的SMC控制器设计

SMC的一般设计过程分为两步：先设计切换函数；再设计控制律。本节首先基于趋近律构造一种直观有效的SMC系统：采用极点配置法设计切换函数以得到期望的滑动模态，采用趋近律设计控制律以得到较好的趋近过程动态特性。

2.1 设计过程

a）切换函数设计。

设计目标为：对于运载器模型（式（2）），选择切换函数为

b）控制律设计。

设计目标为求滑模变结构控制：

c）滑模稳定性证明。

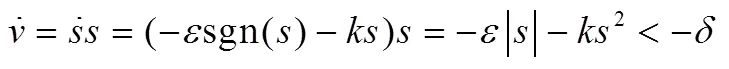
2.2 参数选取

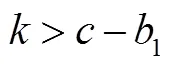
2.3 三自由度小偏差仿真

a）理想状态仿真。

采用上述方法对所设计的基于趋近律的理想SMC控制器进行仿真验证，仿真初始条件为

仿真结果如图1所示。

从图1可以看出：

3）下偏差状态下，初始阶段发动机喷管摆角出现明显振荡，摆动角速度较大，最大为57（°）/s，发动机喷管摆角最大值为4.14°。

b）降抖状态仿真。

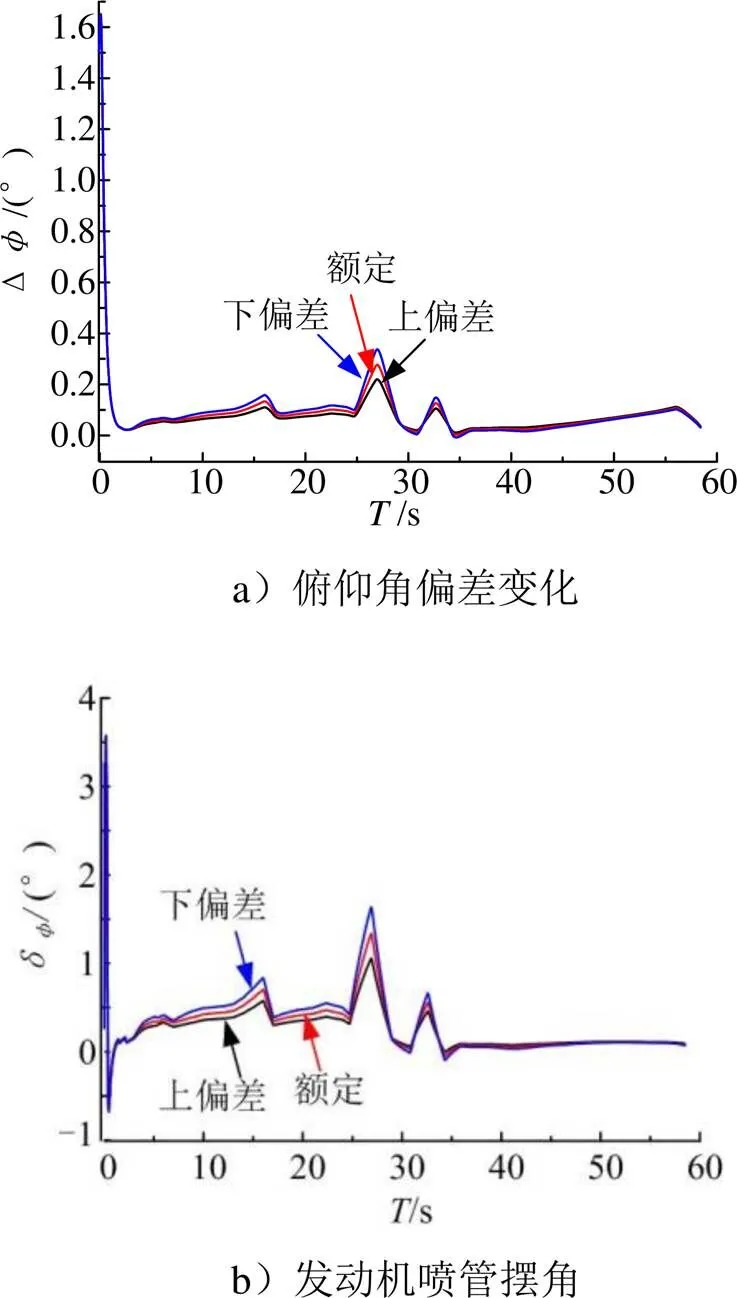
图2 基于趋近律的降抖SMC控制器仿真结果（m）

从图2可知：

2）额定状态下，系统经过约2.1 s到达准滑动模态平衡点，俯仰角偏差对外部干扰具有一定不变性，但在外部干扰较大的时间段仍然出现较小波峰，一级飞行段结束时刻误差为0.03°；

3）3种偏差状态下的俯仰角偏差变化曲线差别较小，初始阶段发动机喷管摆角均未出现振荡，摆角最大值为3.59°。

c）边界层厚度的影响。

3 基于干扰上界的SMC控制器设计

3.1 设计过程

考虑外部干扰和参数摄动等不确定性的运载器主动段俯仰通道动力学模型可表示为

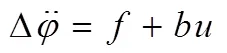
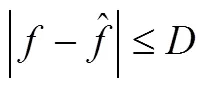
a）切换函数设计。

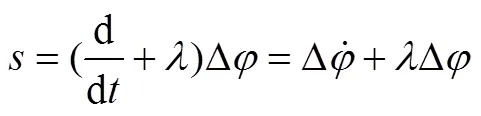
则有：

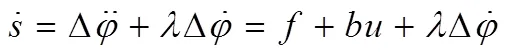
b）控制律设计。

设计如下控制律[5]：

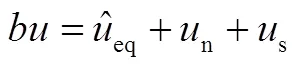
c）滑模稳定性证明。

满足滑动模态到达条件。

3.2 干扰上界

根据干扰模型仿真得到俯仰通道干扰力矩系数如图3所示。可知干扰力矩曲线呈马鞍状，在17～40 s内较大。

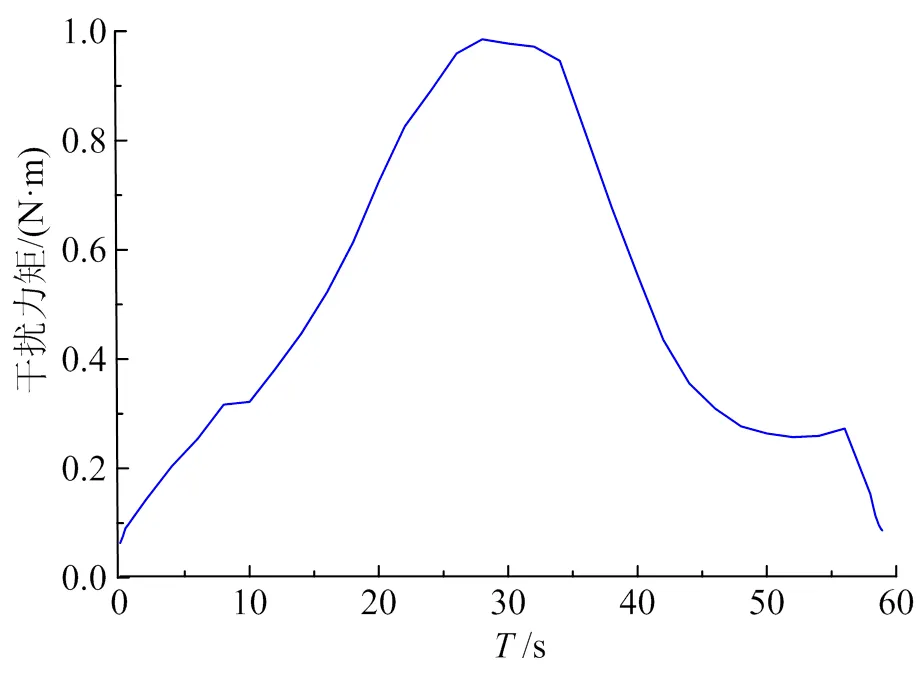
图3 俯仰通道总干扰力矩

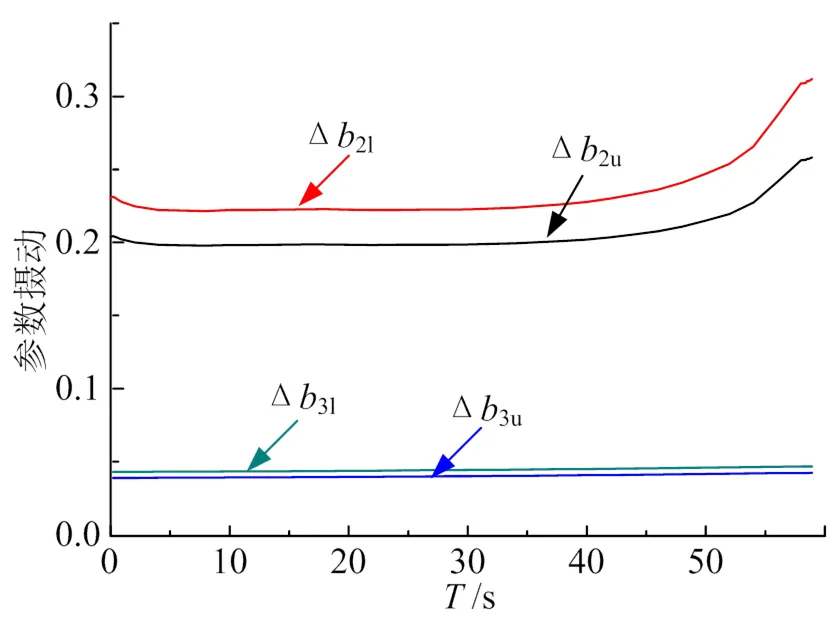
图4 俯仰通道参数摄动

3.3 三自由度小偏差仿真

Tab.1 Design Result of

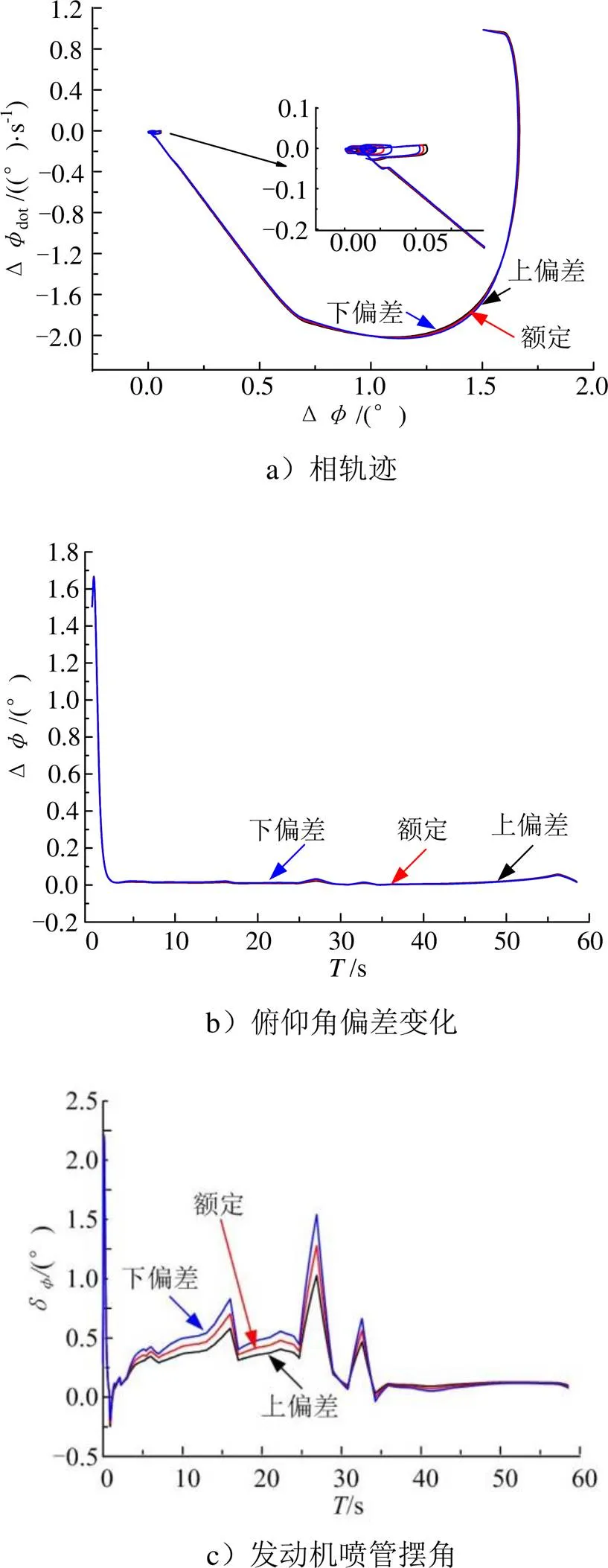
图5 基于干扰上界的降抖SMC控制器仿真结果（m）

仿真结果表明：

b）3种偏差状态下，趋近过程和滑动模态的俯仰角偏差曲线均差别甚微，说明控制器鲁棒性良好；

c）进入滑动模态后，系统对外部干扰的不变性较好，几乎不受外部干扰影响，一级飞行段结束时刻俯仰角偏差误差为0.01°；

d）发动机喷管摆角的最大值出现在初始阶段，为2.21°，且喷管摆动角速度较小，未出现振荡。

4 结 论

本文探索了两种基于滑模的SMC技术在运载器主动段俯仰通道姿控系统设计中的工程应用，得到如下结论：

b）采用边界层方法设计的降抖SMC控制器能够显著降抖，但仿真结果对边界层厚度比较敏感，工程应用时需要合理选择边界层厚度；

c）基于干扰上界的SMC控制器通过精细化设计实现了降低不连续切换项系数的要求，在所选择的设计参数和边界层厚度状态下，仿真结果表明控制器的鲁棒性良好，稳态误差小，同时发动机喷管摆角需求较小。

[1] Slotine J–J E, Li W. Applied nonlinear control[M]. Prentice Hall： Englewood Cliffs, NJ, 1991: 62-71.

[2] Young K D, Utkin V I. A control engineering’s guide to sliding mode control[J]. IEEE, Transactions on Control Systems Technology, 1999, 7(3): 328-342.

[3] 徐延万, 等. 控制系统设计(上)[M]. 北京: 宇航出版社, 1991: 119-129.

Xu Yanwan, et al. Control system design[M]. Beijing: Astronautics Press, 1991: 119-129.

[4] 贾沛然, 陈克俊, 何力. 远程火箭弹道学[M]. 长沙: 国防科技大学出版社, 1993: 67-71.

Jia Peiran, Chen Kejun, He Li. Long-range rocket ballistics[M]. Changsha: National University of Defense Technology Press, 1993: 67-71.

[5] 高为炳. 变结构控制的理论及设计方法[M]. 北京: 科学出版社, 1996: 96-103.

Gao Weibing. Theory and design method of variable structure control[M]. Beijing: Science Press, 1996: 96-103.

[6] 程鹏. 自动控制原理[M]. 北京: 高等教育出版社, 2003: 68-73.

Cheng Peng. Autocontrol theory[M]. Beijing: Higher Education Press, 2003: 68-73.

[7] 梁卓. SINS/GPS制导炸弹变结构制导控制系统设计与研究[D]. 南京: 南京理工大学, 2009.

Liang Zhuo. Design and study of guidance and control system based on variable structure control theory for SINS/GPS guided bomb[D]. Nanjing: Nanjing University of Science & Technology, 2009.

[8] 严浙平. 时变干扰下欠驱动AUV水平面轨迹跟踪的反步滑模控制[J]. 宇航总体技术, 2017, 4(1): 1-7.

Yan Zheping. Backstepping sliding mode control of the under actuated AUV in horizontal plane trajectory tracking tnder the time-varying disturbance[J]. Astronautical Systems Engineering Technology, 2017, 4(1): 1-7.

Design of Launch Vehicle’s Pitching Channel Attitude Control System Based on SMC

Shi Bao-lan, Han Lu, Li Zi-guang, Zhang Guang-yong, Hua Jin

(Beijing Institute of Aerospace Systems Engineering, Beijing, 100076）

Compared with the classical PID control method, sliding mode control (SMC) method can easily take uncertainties into account. The system’s robustness. The engineering application of SMC technology into launch vehicle’s attitude control during boosting phase is issued is increased. Firstly, SMC system based on reaching law is studied and then depressing the discontinuity switching item is required. Secondly, SMC system based on the upper limit of disturbance is analyzed. The control effect of the two methods is evaluated by three degrees of freedom simulation. It’s proved that the second controller performs well in robustness and precision while the control demand of the motor’s nozzle is smaller.

attitude control; sliding mode control; uncertainty; upper limit of disturbance

TP271

A

1004-7182(2020)01-0014-06

10.7654/j.issn.1004-7182.20200103

2018-08-14；

2018-09-18

石宝兰（1988-），女，工程师，主要研究方向为飞行器姿控总体设计与仿真分析。

韩 璐（1989-），男，工程师，主要研究方向为飞行器总体设计。

李紫光（1985-），男，工程师，主要研究方向为飞行器载荷设计。

张广勇（1989-），男，工程师，主要研究方向为飞行器弹道设计。

化 金（1991-），女，工程师，主要研究方向为飞行器弹道设计。