高升阻比滑翔飞行器再入制导方法研究
2020-03-27李天任王宇航雷建长
李天任,黄 佩,王宇航,雷建长
高升阻比滑翔飞行器再入制导方法研究
李天任,黄 佩,王宇航,雷建长
(中国运载火箭技术研究院研究发展中心,北京,100076)
针对高升阻比滑翔飞行器再入段制导方法的工程需求,提出了“改进的预测-校正制导+定向末制导”方法作为再入段制导方法。通过调整其横向制导的误差边界,解决了飞行器在交班点附近出现的横向误差不收敛问题,同时兼顾了较大的横向机动距离,发挥了飞行器高升阻比的特性。对预测-校正制导流程进行了改进,从而赋予了飞行器在线变更目标点的能力。在距目标一定距离时切换为末制导律,采用约束落点弹道倾角和航向角的广义比例导引法,实现对目标的定点定向打击。蒙特卡洛仿真结果表明,该制导方法对各项误差有较强的鲁棒性,具有较好的应用前景。
高升阻比滑翔飞行器;预测-校正制导;末制导;在线变更目标点;蒙特卡洛仿真
0 引 言
升力式再入飞行器制导技术在20世纪70年代经历了第1次发展期,这一时期的研究主要针对航天飞机展开,逐步形成了基于阻力加速度剖面的再入制导方法。在随后的20世纪90年代,在新一代可重复使用运载器的需求牵引下,NASA启动了“先进制导和控制研究计划”,使得升力式再入制导方法研究得到了第2轮快速发展,形成了以Leavitt等[1]为代表的衍化阻力加速度制导方法以及Shen等[2]研究的在线生成三维轨迹的制导方法。
升力式再入飞行器的制导方法可以分为标称轨迹制导方法和预测-校正制导方法。标称轨迹制导方法已经成功应用在航天飞机上,其需要依赖事先规划好的再入轨迹,因此难以满足未来对再入飞行器自主性的要求。预测-校正制导方法始于20世纪80年代,最早用于低升阻比火星探测器的再入制导方法研究,限于当时的计算能力,只能采取解析的方法预测再入轨迹。随着计算能力的逐步提升,采用数值积分进行轨迹精确预测成为可能。Powell[3]于20世纪90年代,针对火星探测任务,采用经典龙格库塔方法进行轨迹数值积分,达到了精确预测再入轨迹的目的。Lu[4]在前人的研究基础上,将各项再入约束条件通过拟平衡滑翔条件引入到倾侧角的解算中,使得预测-校正制导律距离应用更进一步。李惠峰等[5,6]针对可重复使用运载器采用“钟”形横向误差边界进行横向导引,并将各项再入约束条件简化为统一的形式,从而便于解析计算。需要注意的是,上述研究将预测-校正制导律作为返回式航天器的再入制导方法,一般对横向机动距离没有要求,对落点或开伞点的精度需求为千米级,一般以飞行器进入末端能量管理区域作为结束条件,与本文的研究背景有较大区别。
本文采用改进的预测-校正制导律作为高升阻比滑翔再入飞行器的中制导方法,通过分析滑翔飞行器的再入运动规律,将横向制导的误差边界调整为“沙漏”形式,从而缓解了预测-校正制导方法在交班点附近不收敛的问题,同时大幅增加了横向机动距离,使得滑翔飞行器的高升阻比特性得到充分发挥。在飞行末段,采用约束末端弹道倾角和航向角的广义比例导引律进行末制导,同时约束6个落点状态量中的5个。蒙特卡洛仿真结果表明,这种“改进的预测-校正制导律+定向末制导律”方法具有较好的鲁棒性。
1 再入动力学模型
地球为圆球且不旋转。假设下的飞行器动力学方程为[7]
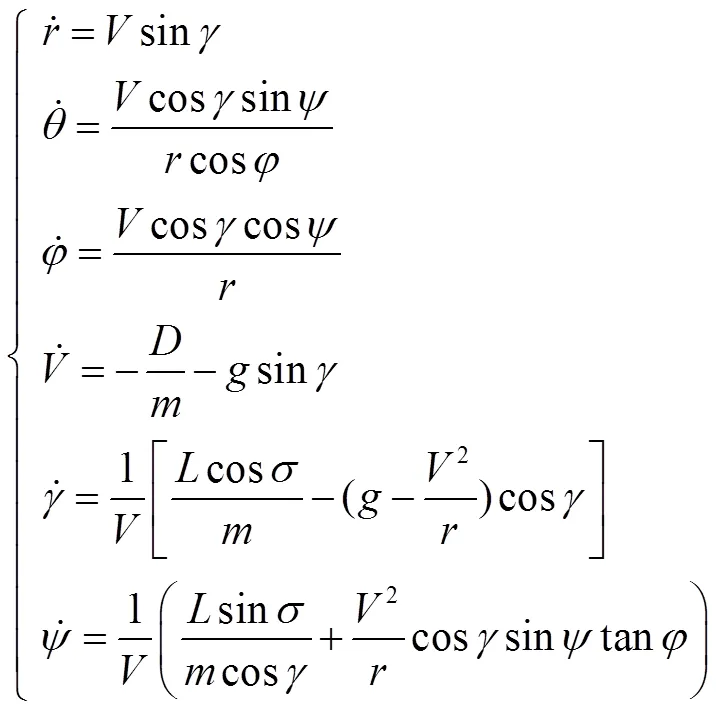
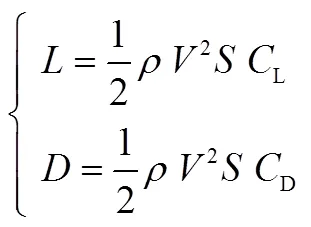
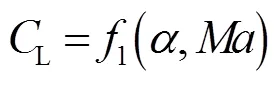
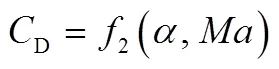
攻角剖面采用Harpold[8]的分段线性攻角方案以降低下降段的峰值热流。
2 预测-校正制导方法
本文采用定攻角剖面的预测-校正制导律作为中制导方法。通过在线调整倾侧角绝对值来满足纵平面内的射程要求,并在给定的侧向误差边界内不断改变倾侧角符号以实现横程误差控制。
2.1 纵向制导
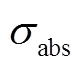
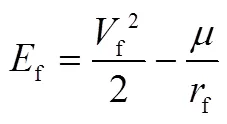
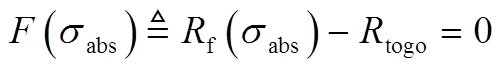
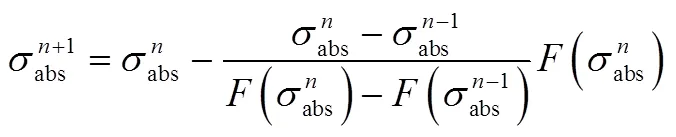
2.2 横向制导
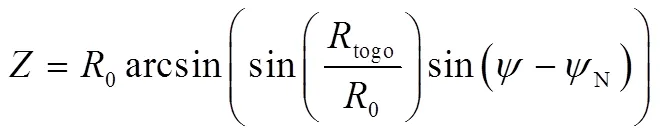
大量数值仿真结果表明,飞行器的横向机动能力随速度、高度的减小而减弱,Shen[9]、张曼[10]、李惠峰[5]等采用线性或“钟”形误差边界可导致滑翔段末段的横向误差无法收敛。此外,线性误差边界严重限制了高升阻比飞行器的横向机动能力,不适合本文的研究背景。将线性误差边界调整为以下的“沙漏”形式:
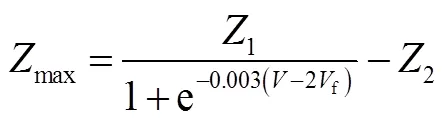
式中 为设计者可以调整的参数,用于控制横程误差边界的幅值。图1是2种横程误差边界示意。
可以发现沙漏形误差边界相比线性误差边界,在高速条件下赋予了飞行器更大的横向机动空间,而在低速时通过梯度较小的边界进行横向导引。
3 末制导方法
3.1 最优制导律
以目标点为原点建立末制导坐标系[12],则末制导需要实现的终端约束为
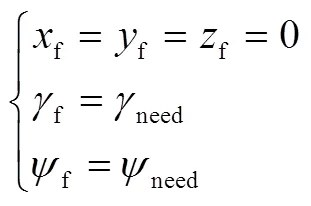
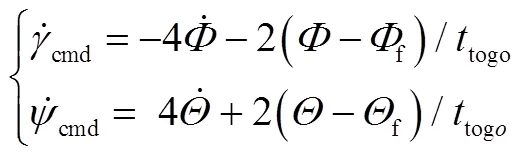
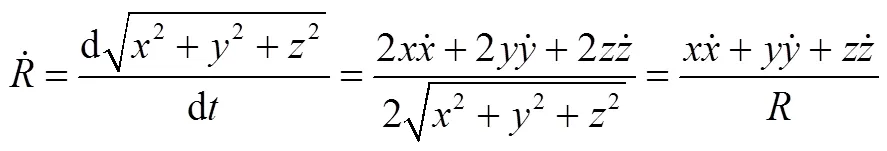
3.2 控制量求解
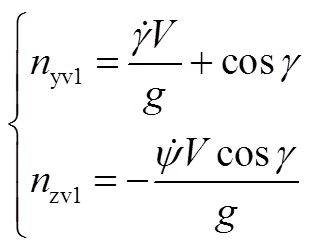
总法向过载为
4 数值仿真及分析
4.1 可行性验证
通过数值仿真,对“预测-校正制导+定向末制导”方法进行可行性验证。仿真计算均遵循以下假设条件:
b)飞行器可达区已知,目标点在可达区域内;
仿真硬件为Intel Core i7-3770 CPU, 3.40 GHz, 在Matlab 环境下编写代码,具体仿真参数如下:
f)预测-校正制导的迭代周期取20 s,弹目斜距小于200 km时迭代周期变为5 s;
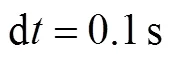
h)末制导的制导周期为0.1 s。
数值仿真结果如图2~4所示。
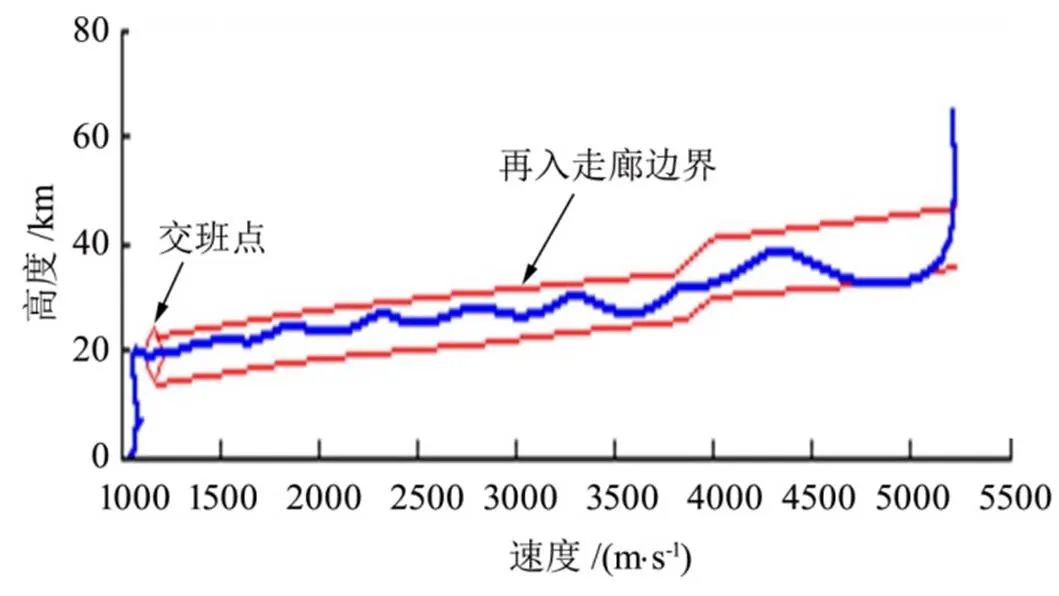
图2 速度-高度曲线
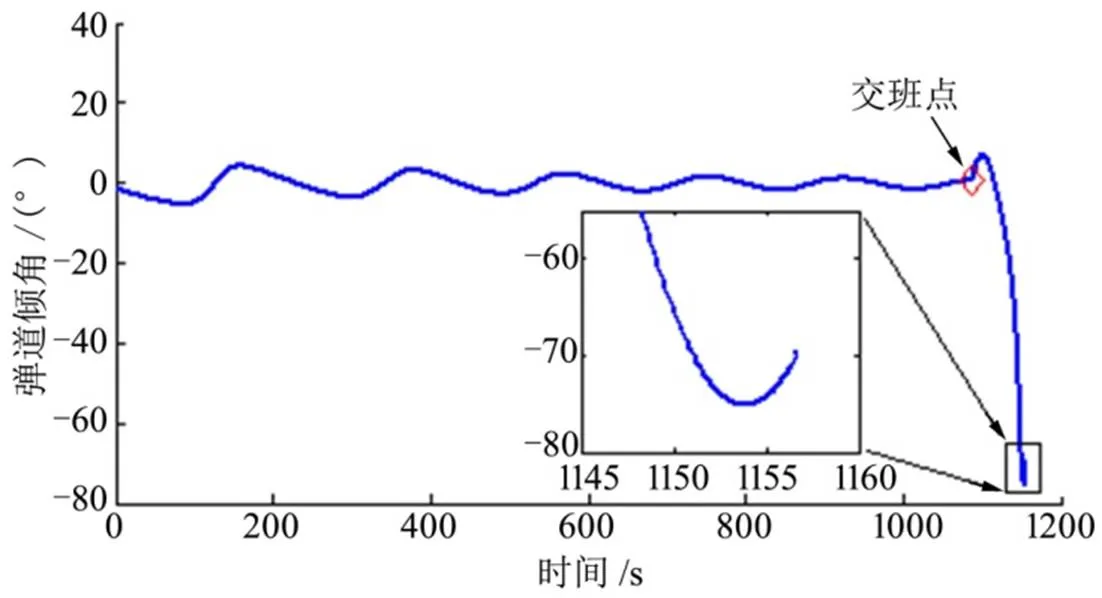
图3 时间-弹道倾角曲线
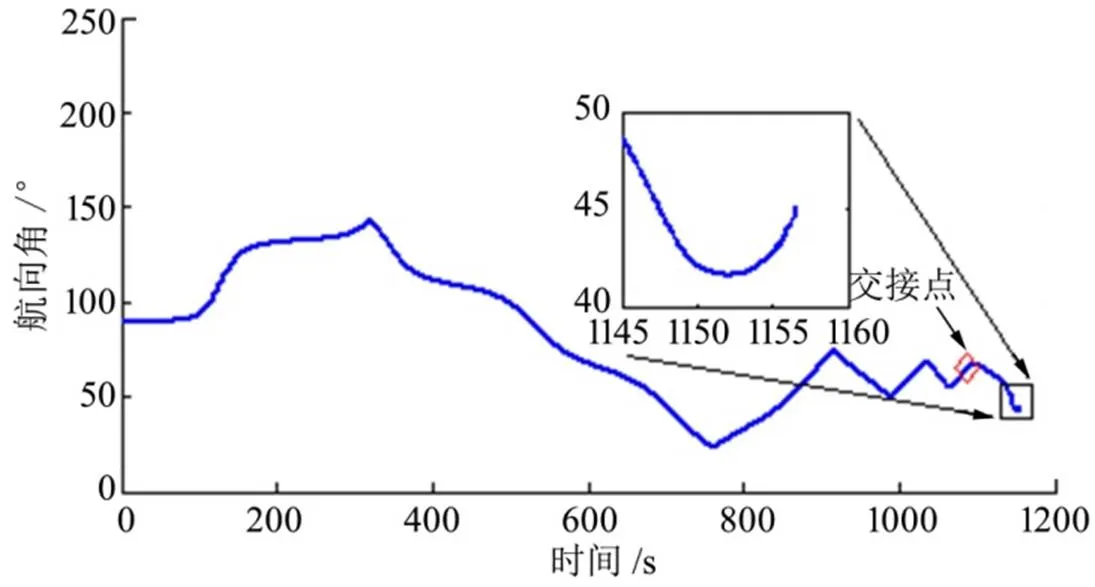
图4 时间-航向角曲线
4.2 鲁棒性分析
为分析“预测-校正制导+定向末制导”方法的鲁棒性,采用最大偏差法(包括正向和负向最大偏差)随机生成500组误差,进行蒙特卡洛模拟打靶。考虑的误差见表1。
表1 误差模型
Tab.1 Error Model
误差种类误差分布类型误差大小(3) 再入速度/(m·s-1)高斯分布100 再入弹道倾角/(°)均匀分布0.1 再入航向角/(°)均匀分布0.1 再入点高度/ km高斯分布1 再入点经度/(°)高斯分布0.1 再入点纬度/(°)高斯分布0.1 升力系数高斯分布20% 阻力系数高斯分布20% 大气密度高斯分布30%
图5~7给出了最大误差条件下的打靶结果。结果表明,“预测-校正制导+定向末制导”方法使飞行器末端位置及两个速度角收敛到指定值。落点位置偏差均在0.4 m以内,末端弹道倾角及航向角偏差均不超过0.04°,说明该制导方法对各类误差的鲁棒性较强。
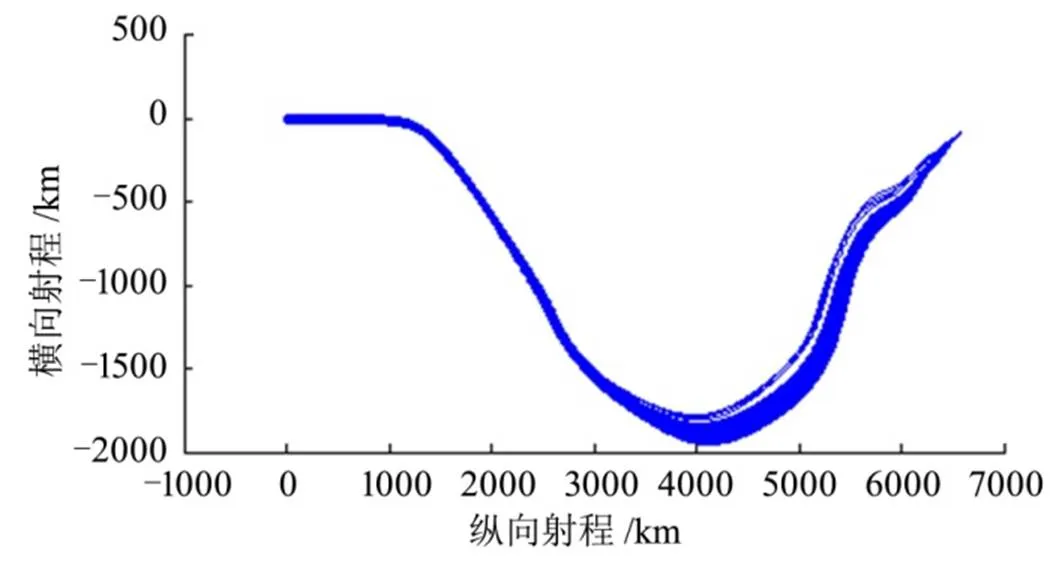
图5 最大误差条件下的地轨迹
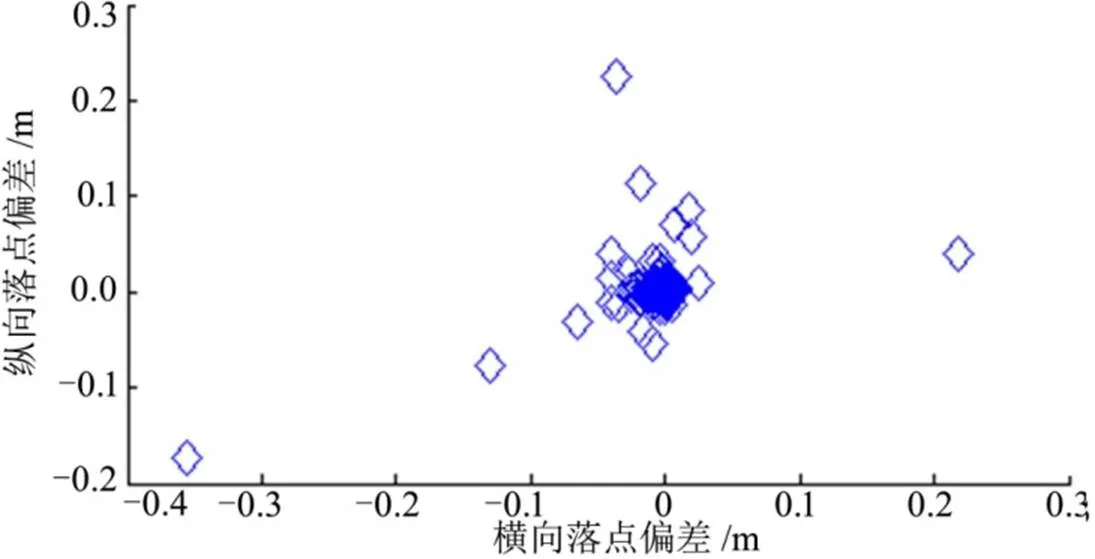
图6 落点位置误差分布
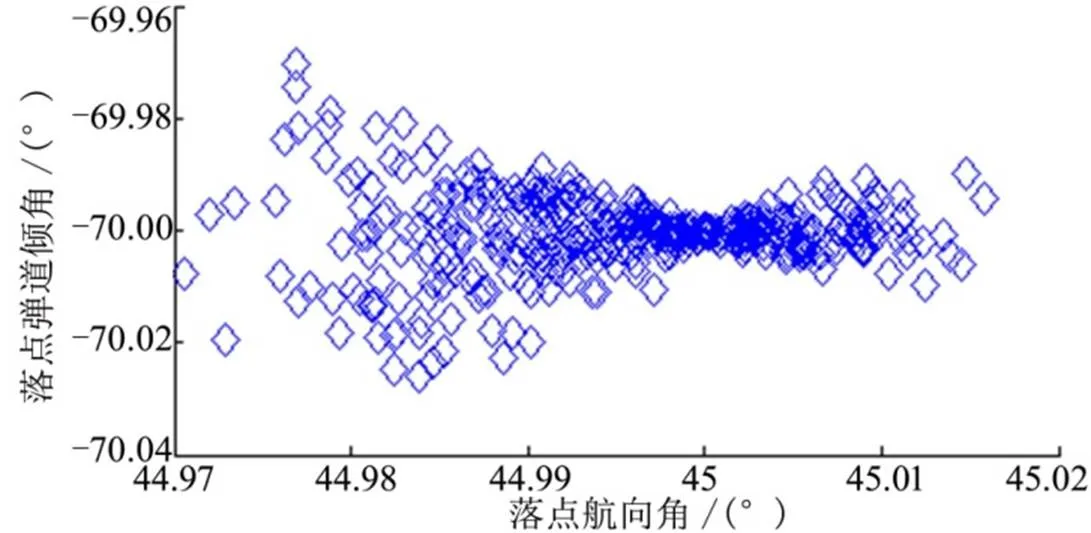
图7 落点角度误差分布
4.3 预测-校正制导性能分析
预测-校正制导律多用于水平降落的可重复使用飞行器,其制导性能一般通过倾侧翻转次数、是否能将飞行器引导进末端能量管理区域等指标来描述。而本文的研究对象没有水平降落要求,无需作为预测-校正制导律的末端约束,仅需满足末制导律交班要求即可;此外,为了发挥高升阻比滑翔飞行器的强机动能力,制导律不能使其频繁翻转。
本文通过改进横向制导的误差边界,增加了飞行器横向机动距离,同时避免了交班点附近可能出现的误差不收敛情况,改进前后的对比如图8~10所示。
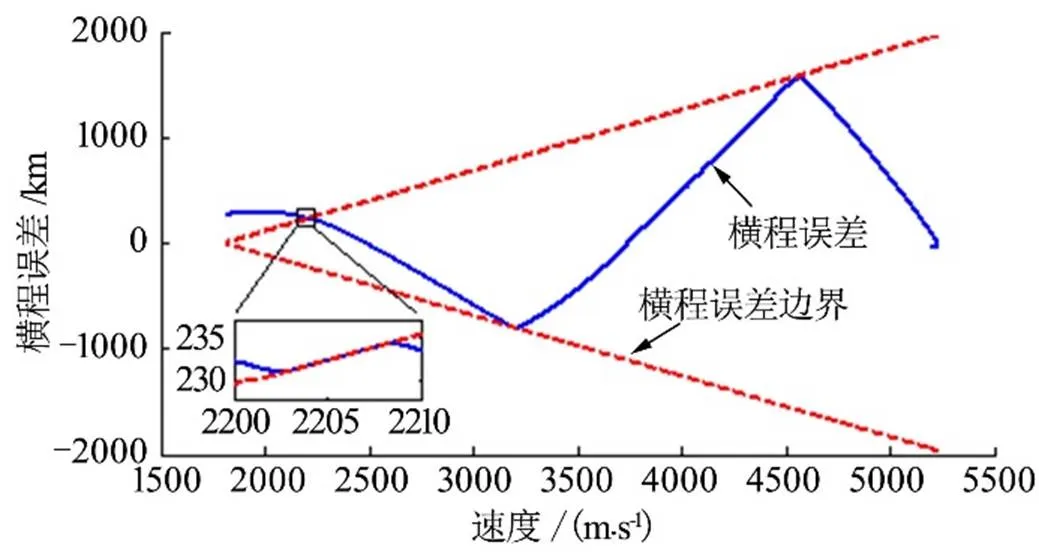
图8 采用原横程误差边界
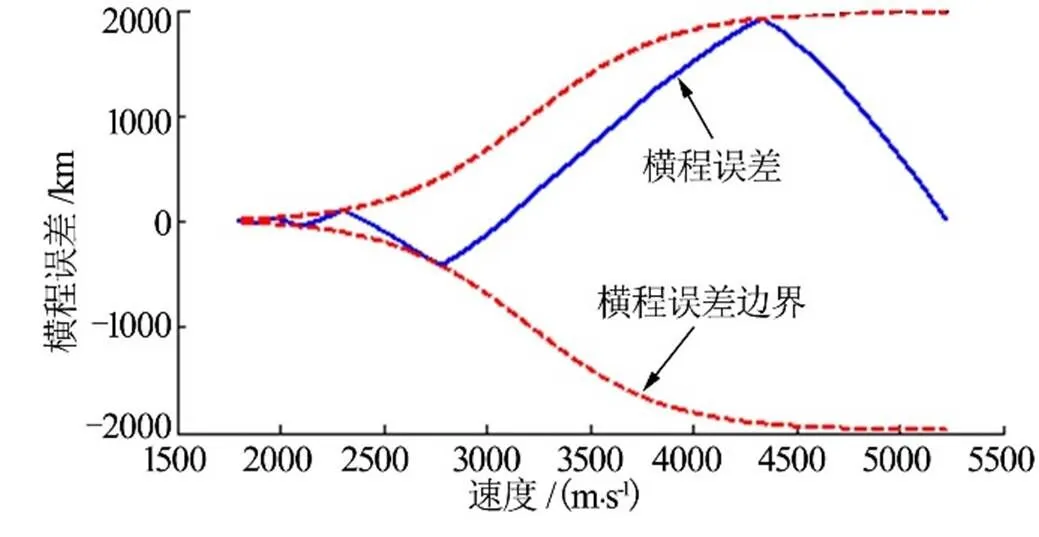
图9 采用改进的横程误差边界
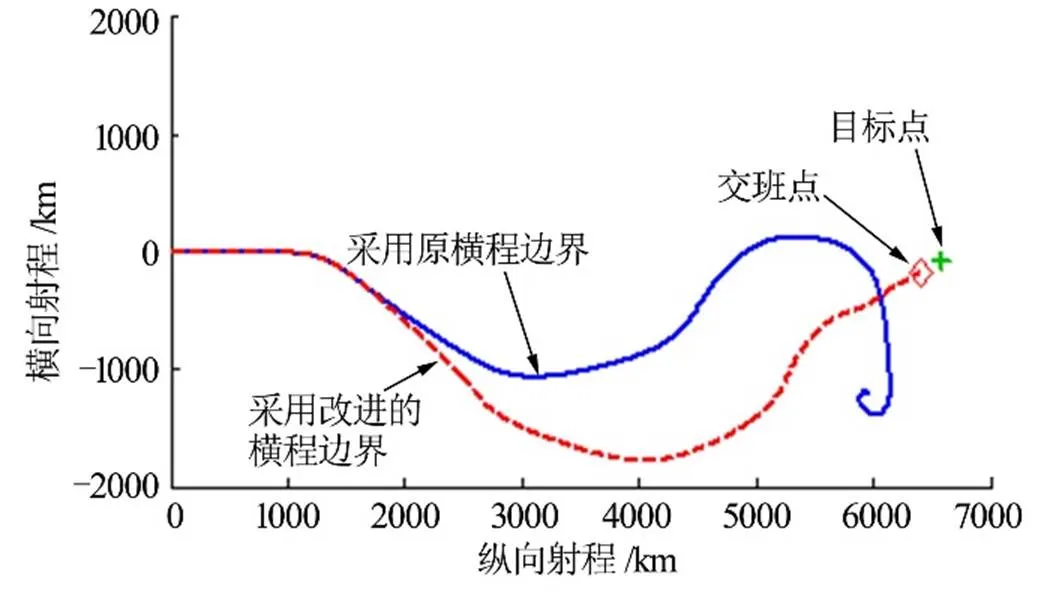
图10 轨迹对比
仿真结果表明,采用原误差边界,由于飞行器速度降低后横向机动能力减弱,横程误差斜率减小,误差斜率小于误差边界斜率,翻转逻辑失效,导致预测-校正末段横程误差无法收敛;采用改进的沙漏形误差边界则可避免该问题。新的横程误差边界使横向机动距离增加近一倍,发挥了高升阻比飞行器升力大、机动能力强的优势。从制导原理上分析,纵向制导已经决定了倾侧角幅值,实际上也就决定了横程误差斜率,若当前横程误差边界斜率大于前者,可能会导致横程误差始终无法收敛。即使调整翻转逻辑,这一问题也不会得到解决,只能调整误差边界形式。
预测-校正制导过程中在线变更目标,结果如图11所示。
目标1、目标2的经度、纬度分别为[59.2637°,-0.666135°]、[65.8206°,-7.95380°],两者球面距离为1088.8 km。结果表明该制导律仍然能够有效工作,但是在线变更目标会造成横向误差的瞬时突变,若横向误差跳出误差边界,则可能导致横向制导逻辑失效。为解决该问题,对预测-校正制导逻辑进行修正,修正后的横向制导流程见图12。
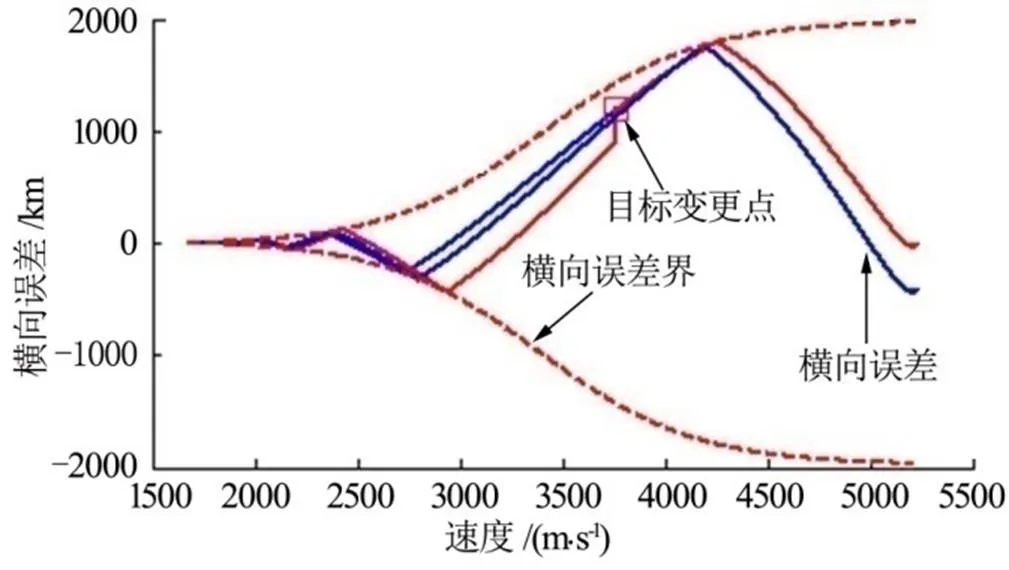
图11 在线变更目标点形成的横向制导结果
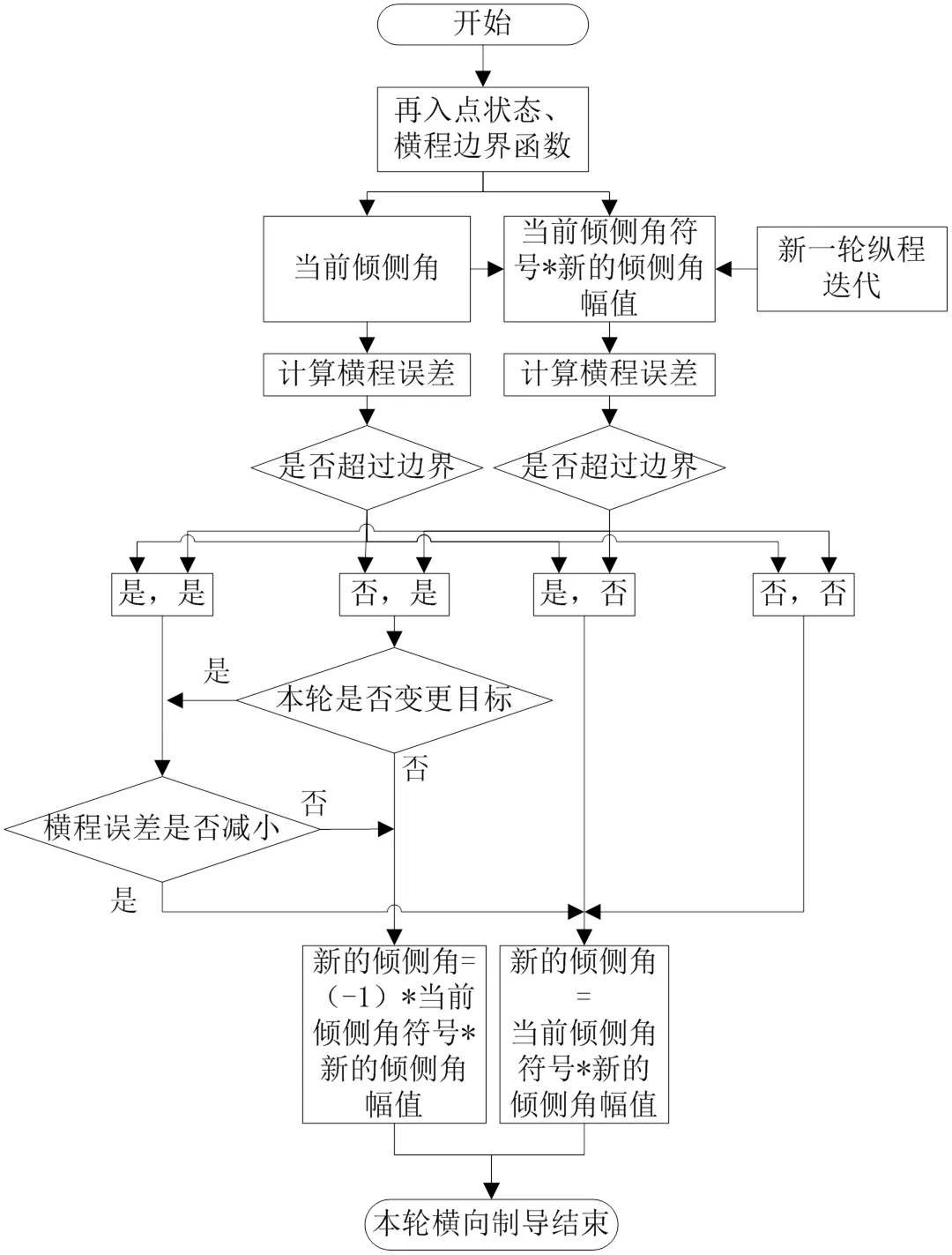
图12 修正后的横向制导流程
新的横向制导流程不仅依赖横程边界来施加翻转逻辑,还增加了“横程误差是否减小”的逻辑判断,用于判定当前的倾侧角符号是否有利于飞行器回到误差边界内。新的横向制导流程能够有效应对在线变更目标的情况,但仍需要注意的是,若目标选取的位置超出了当前的可达区域,预测-校正制导律则会失效。
4.4 末制导性能分析
本文采用约束落点弹道倾角和航向角的广义比例导引法作为末制导方法,同时约束6个落点状态量中的5个,实现对目标的定点定向打击。不同落点角度约束的末制导轨迹如图13所示。
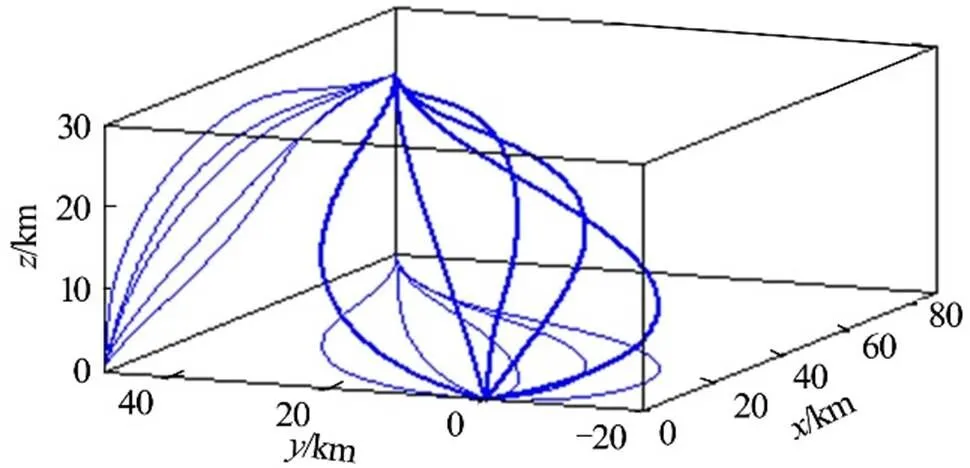
图13 不同落点角度约束的末制导轨迹
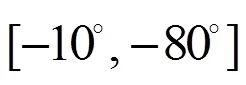
5 结 论
以“改进的预测-校正制导律+定向末制导律”作为高升阻比滑翔飞行器再入段制导方法。针对预测-校正制导律在交班点附近可能出现的状态不收敛的问题,分析了原因并提出解决方法。通过调整横向制导的误差边界,有效解决了上述问题,同时兼顾了较大的横向机动距离。改进后的预测-校正制导流程赋予了飞行器在线变更目标点的能力。本文在飞行末段采用广义比例导引法,同时约束落点弹道倾角和航向角,实现对目标的定向打击。打靶仿真结果表明,这种制导方法对各项误差有较强的鲁棒性,具有较好的应用前景。
[1] Leavitt J A, et al. Performance of evolved acceleration guidance logic for entry[C]. Monterey, California, USA: AIAA Guidance, Navigation, and Control Conference and Exhibit, 2002.
[2] Shen Zuojun, Lu Ping. Onboard generation of three-dimensional constrained entry trajectories[J]. Journal of Guidance, Control and Dynamics, 2003, 26 (1): 111-121.
[3] Powell W R. Numerical roll reversal predictor-corrector aerocapture and precision landing guidance algorithm for the Mars surveyor program 2001 missions[C]. Boston, Massachusetts, USA: AIAA Atmospheric Flight Mechanics Conference Boston, 1998.
[4] Lu Ping. Predictor-corrector entry guidance for low-lifting vehicles[J]. Journal of Guidance, Control and Dynamics, 2008, 31(4): 1067-1075.
[5] 李惠峰, 谢陵. 基于预测-校正方法的RLV 再入制导律设计[J]. 北京航空航天大学学报, 2009, 35(11): 1344-1348.
Li Huifeng, Xie Ling. Reentry guidance law design for RLV based on predictor-corrector method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(11): 1344 -1348.
[6] Li Huifeng, Zhang Ran, Li Zhaoying, Zhang Rui. New method to enforce inequality constraints of entry trajectories[J]. Journal of Guidance, Control and Dynamics, 2012, 35(5): 1662-1667.
[7] Vinh N X, et al. Hypersonic and planetary entry flight mechanics[M]. Ann Arbor MI: University of Michigan Press, 1980.
[8] Harpold J C, Graves C A. Shuttle entry guidance[J]. The Journal of the Astronautical Sciences, 1979, 37(3): 239-268.
[9] Shen Zuojun, Lu Ping. Dynamic lateral entry guidance logic[J]. Journal of Guidance, Control and Dynamics, 2004, 27(6): 949-959.
[10] 张曼. 可重复使用运载器预测校正再入制导研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.
Zhang Man. Predictor corrector reentry guidance for reusable launch vehicles[D]. Harbin: Harbin Institute of Technologh, 2013.
[11] 程国采. 弹道导弹制导方法与最优控制[M]. 长沙: 国防科技大学出版社, 1987.
Cheng Guocai. Guidance method and optimal control of ballistic missile[M]. Changsha: National University of Defense Technoogy Press, 1987.
[12] 陈克俊, 赵汉元. 一种适用于攻击地面固定目标的最优再入机动制导律[J]. 宇航学报, 1994, 15(1): 1-8.
Chen Kejun, Zhao Hanyuan. An optimal reentry maneuver guidance law applying to attack the ground fixed target[J]. Journal of Astronautics, 1994, 15(1) : 1-8.
[13] 黄佩, 王泽, 郝颖, 周华, 雷建长. 带落角约束的高超声速飞行器轨迹仿真研究[J]. 导弹与航天运载技术, 2015 (1): 1-4.
Huang Pei, Wang Ze, Hao Ying, Zhou Hua, Lei Jianchang. Study on trajectory simulation of hypervelocity vehicle with impact angle constraint[J]. Missles and Space Vehicles, 2015 (1): 1-4.
Research on Reentry Guidance Method for High L/D Gliding Vehicles
Li Tian-ren, Huang Pei, Wang Yu-hang, Lei Jian-chang
(Research & Development Center, China Academy of Launch Vehicle Technology, Beijing, 100076)
Aiming at the engineering requirement of the entry guidance method of the high lift-draft ratio gliding vehicle, the “improved predictor-corrector guidance + directional terminal guidance” method is proposed as the guidance method. By adjusting the error boundary of its lateral guidance law, the problem that the lateral error of the vehicle near the shift point does not converge is solved, the large cross-range and the characteristics of the high lift-draft ratio is taken into account. The author improves the predictor-corrector guidance process and gives the vehicle the ability to change target point online. When the target is close enough to the vehicle, the constrained ballistic angle and heading angle of the generalized proportional guidance method is used to achieve striking the target accurately. Monte Carlo simulation results show that the guidance method has strong robustness to each error and has good application prospect.
high L/D gliding vehicle; predictor-corrector guidance; terminal guidance; change target online; Monte Carlo simulation
V448
A
1004-7182(2020)01-0060-06
10.7654/j.issn.1004-7182.20200111
2018-07-28;
2018-12-25
李天任(1993-),男,助理工程师,主要研究方向为飞行器制导与控制。
黄 佩(1990-),男,工程师,主要研究方向为飞行器制导与控制。
王宇航(1982-),男,高级工程师,主要研究方向为飞行器制导与控制。
雷建长(1970-),男,研究员,主要研究方向为飞行器总体设计。
