基于轨道倾角约束的小行星探测弹、轨道拼接设计研究

张博戎，马 英，周天帅，何 巍，容 易

基于轨道倾角约束的小行星探测弹、轨道拼接设计研究

张博戎，马 英，周天帅，何 巍，容 易

（北京宇航系统工程研究所，北京，100076）

设计一个完整的小行星探测轨道方案需要分别对整条轨迹中的弹道段和轨道段进行优化并拼接。目前拼接设计方法中对弹道段终点约束考虑不足、设计效率低。基于实际弹道运算数据计算了指定运载火箭发射弹道对停泊轨道倾角的约束形式，并研究了火箭偏航能力和射向变化对弹道-轨道拼接后无量纲运载能力的影响。结果表明，算例中的健神星探测窗口不适合低轨道倾角发射弹道。考虑一般情况，高轨道倾角发射弹道可以更好适应飞出地球引力影响球的深空探测类任务需求。根据研究结果，提出了对未来深空探测运载火箭的设计需求。

运载火箭；发射能量；轨道倾角；小行星探测；弹道-轨道拼接

0 引 言

深空探测对于人类认知宇宙世界具有重大意义。目前，小行星等一类小天体逐渐成为人类深空探测的热点之一[1]。在小行星探测领域，美国、俄罗斯、日本、欧洲等均有任务开展，并取得了丰硕成果，中国除去嫦娥二号利用剩余燃料飞越近地小行星图塔蒂斯以外，暂无针对小天体的探测实例[2]。

随着小行星探测的意义逐渐增强，中国有必要详细规划相应的探测任务。弹、轨道优化是航天任务规划中的先行工作，一个快速、高效的弹、轨道优化设计方法可以为深空探测任务规划提供极大帮助和关键依据[3]。深空段轨道的全局优化是一个复杂问题[1]，此外也应注意到，探测器在深空飞行的轨道只是全段轨迹的一部分，主动段弹道设计也是深空探测弹轨道全局优化中的重要环节。

目前，大部分深空轨道优化设计研究将地球出发条件简化为从日心系中的一个质点以给定速度（或给定发射能量）出发[4]，也有部分研究将地球出发条件限定在指定高度近地轨道上的任意一点[5]，并对轨道倾角进行一定范围约束[6]。这也说明现有研究已经开始关注于轨道出发点能否与地球出发的弹道成功拼接。进一步精细考虑弹、轨道拼接的约束形式，以上约束方法均与实际发射情况存在差别，受限于发射场地理位置、火箭射向、滑行能力等因素，实际出发窗口更会远小于简化处理后的范围。虽然在实际工程任务设计中，可以调整火箭飞行程序以匹配探测器出发条件，但这一手段也无法满足所有出发条件，且会损失运载能力。目前仍未有方法可以从全局角度有效解决火箭和深空探测器的弹、轨道联合优化设计问题，对这一问题进行系统分析具有很强的工程实际意义。

1 模型与方法

深空探测任务的典型飞行过程一般是由运载火箭将火箭末级和有效载荷的组合体运送至近地停泊轨道（Low Earth Orbit，LEO），滑行至合适位置时，再进行末级点火和星箭分离，使有效载荷具有能够摆脱地球引力的速度。在深空探测任务中，轨道优化是设计主体，弹道能力是先决条件。下文将分别简述轨道优化设计和弹道优化设计的特点与约束，再探究弹、轨道联合优化设计方法。

1.1 轨道模型的特点与约束

小行星探测任务规划的初期，往往需要对多个可能的探测目标进行考察，在一定时间范围内寻找多个可行的初步轨道方案。轨道优化设计均须明确出发条件，也就是航天器飞离地球的约束。

以基于脉冲推进的圆锥曲线拼接方法为例，设计探测器在日心系飞行的轨道时，一般会将地球出发条件简化为在一个点上以指定速度dpt出发。在地球引力影响球（Sphere of Influence，SOI）内选择合适的拼接点，可以将深空轨道与近地停泊轨道用一段双曲线连接，继而算得探测器从停泊轨道上的出发速度和轨道根数要求，这些要求也是下一步进行弹道优化的约束条件。弹道-轨道在地球引力影响球内拼接示意如图1所示。

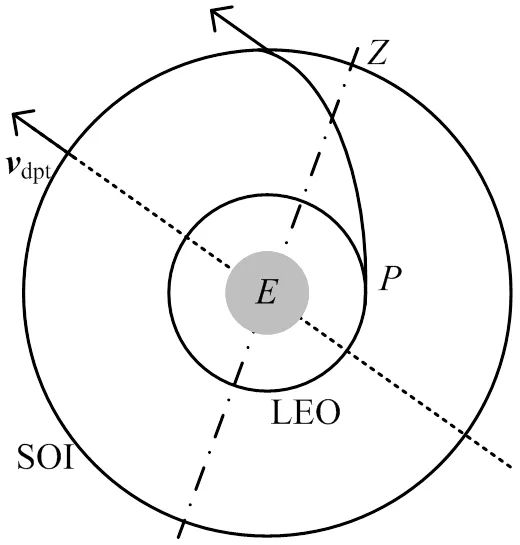
图1 弹道-轨道在地球引力影响球内拼接示意

轨道寻优传统方法大多只以发射能量为约束。考虑在停泊轨道上的加速脉冲和原速度方向一致 （文献[7]已说明这种加速方式的合理性），则发射能量可与从停泊轨道上出发的加速脉冲一一对应，因而轨道优化既可以选择从引力影响球边缘出发为起点，也可以选择从近地停泊轨道出发为起点。在只考虑发射能量约束的情况下，这2种设计方法也是一一对应的。

如果轨道寻优已经找到最优的出发速度矢量dpt，则可以求得其与地球惯性坐标系轴夹角dpt，将其定义为出发速度角。在满足出发速度角不变的情况下，飞出地球引力影响球的一簇双曲线可以围绕dpt所在虚线轴方向任意旋转。由几何关系易知，这要求停泊轨道倾角所在范围为

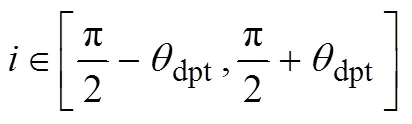
式中为停泊轨道的轨道倾角。

式（1）即可视为轨道出发条件对弹道终点所达停泊轨道倾角的约束，如果弹道终点满足式（1）要求，则弹、轨道具有能进一步完成拼接的可能，如果无法满足要求，则弹、轨道肯定无法完成拼接，需要另行选择轨道设计方案。

1.2 弹道模型的特点与约束

发射深空探测器的运载火箭末级一般具有多次点火和滑行能力。在工程实际中，发射约束一般有以下几种类别：a）能量约束，运载火箭可携带的推进剂有限，因此有效载荷能够达到的发射能量存在上限；b）位置约束，绝大部分运载火箭的发射场处于固定地理位置，起飞射向有范围限制，因此进入停泊轨道的位置是停泊轨道球面上的一条小弧段；c）速度方向约束，停泊轨道可实现的轨道倾角受限于发射场纬度和射向，火箭末级或探测器从停泊轨道加速逃逸的速度脉冲一般沿速度方向施加，因此可以说由于纬度和射向约束，探测器并非可以从任意方向飞离停泊轨道；d）停泊轨道高度约束。由于大气密度和辐射带影响，各国运载器停泊轨道高度一般处于180~400 km范围内[7]，这一高度相比地球半径为小量，因此影响不大。

需要注意的是，针对指定型号的运载火箭，其出发弹道在考虑以上各项约束后，能够从近地停泊轨道出发的“窗口”十分有限。在地球固连坐标系下，这一窗口可以理解为与发射场地理位置相对应的空间“封闭曲面”，从发射场出发的运载火箭，其主动段弹道末端位置（即停泊轨道入轨点）只可能位于这一曲面上。进而将发射曲面转化到地球惯性坐标系下描述，需要引入时间变量，对于特定高度的停泊轨道，该窗口可以理解为是这一轨道高度球面上的一块由发射时刻L、赤经、赤纬圈定的“封闭曲面”，且在该封闭曲面上，每一个出发点的速度矢量Δ2也存在约束，是一个多维相空间中的出发窗口。

1.3 弹道-轨道联合优化设计方法

在深空探测任务规划论证中，通常独立进行弹道-轨道优化设计，需要双方反复针对星箭分离点条件进行迭代，直至满足所有约束，存在迭代过程冗长、效率低的缺点。将星箭分离点加强为时间和空间上的一点约束，限制了全系统方案的优化空间。

如果事先明确运载火箭弹道终点的出发约束，就可以将其转化为约束条件纳入轨道全局优化，由此得到的结果能直接满足指定型号运载火箭的出发条件，不需循环迭代。此方法可以大幅提高总体设计效率，并更易寻得符合工程实际的全局最优方案。

如果无法完全描述弹道终点的约束形式，则可以提出折中的部分联合优化设计方法，即先将运载火箭弹道需要满足的一部分简化条件纳入全局优化，得到结果后再进行精细设计。这一方法虽然仍需循环迭代，但相比原始的独立方法更高效，且易于实现。

如果希望在初步设计阶段就能直接找到满足倾角约束的弹、轨道拼接方案，则可以将基于指定型号运载火箭发射能力的实际弹道计算数据折算为罚函数Pen，将其纳入全局优化，以控制寻优过程：

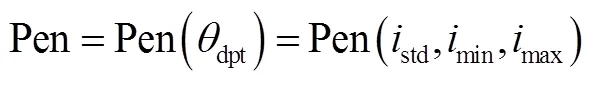
式中max，min分别为该型运载火箭在固定射向发射时能够达到的最大、最小值；std为该型火箭该射向发射时不施加偏航可以到达的标准停泊轨道的轨道倾角值。以上三者和dpt的换算关系可由式（1）获得。通过这一约束得到的全局寻优结果可以直接满足出发弹道倾角约束，避免在接口参数上反复迭代，使设计效率得以提升。第2节中将通过具体算例说明这一方法的科学性。

2 算例与结果分析

2.1 探测目标选取

考虑以小行星带中第4大天体健神星（Hygiea）为探测目标，分析从地球出发至健神星的单圈直接转移轨道。选取出发时间范围为2020年1月1日至2024年12月31日，飞行时间范围为200~1000天。通过求解兰伯特问题，可画出发射速度增量的Pork-Chop图。计算使用的健神星轨道根数数据如下：时刻约化儒略日为2 458 400.5，轨道半长轴469 882 423.9 km，轨道偏心率为0.001 964 944，轨道倾角为0.475 869 838 rad，升交点赤经为4.942 929 521 rad，近地点的幅角为5.449 371 71 rad，平近点角为2.039 696 484 rad。地球出发至健神星出发速度增量等高线如图2所示。

图2 地球出发至健神星出发速度增量等高线

由图2可以看出，从地球出发至健神星的直接发射窗口约每3年多会出现2个能量较低的转移时机，分别对应长弧段和短弧段的轨道方案，这一规律与普遍认知相符。

2.2 弹轨道拼接对运载能力的影响分析

进一步分析能量较低的2020年转移窗口，根据第1节中定义，可以计算每一个出发速度对应的角度约束，画出在此窗口下的dpt等值线，如图3所示。

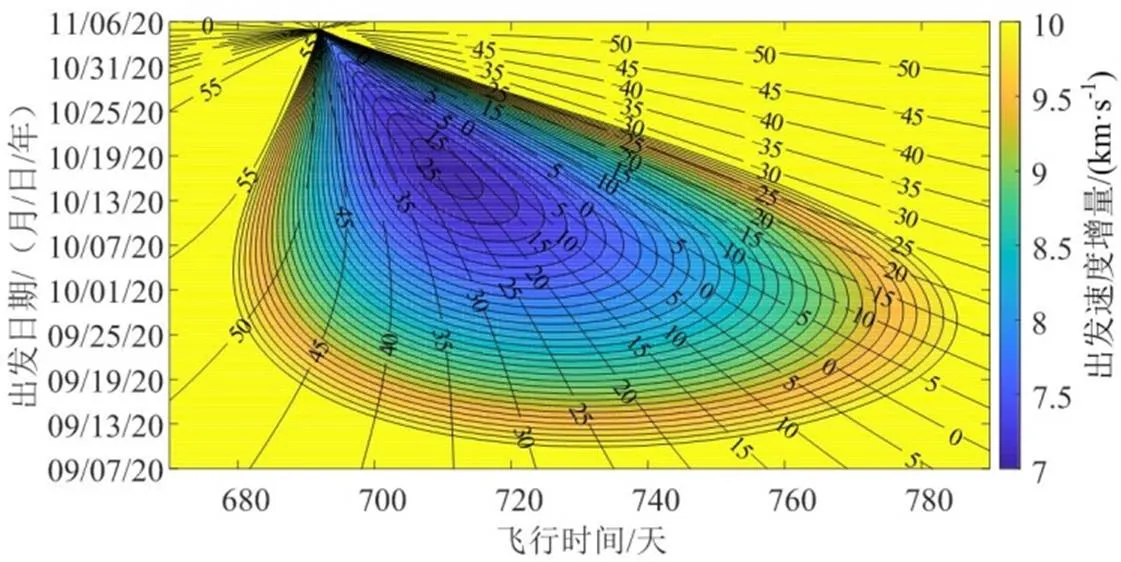
图3 地球至健神星2020年窗口出发速度增量与出发速度角

由图3可看出，针对该窗口的发射机会，如果只考虑发射速度小于7.1 km/s的深色区域，则出发速度角的取值范围约为15~27°，由式（1）知，对应于停泊轨道倾角的可选范围约为63~117°。如果运载火箭的发射能力无法满足这一约束，则意味需要损失运载能力去满足这一窗口[8]，或者选择其他窗口。

选定一型运载火箭执行图3中窗口的发射任务，受限于内陆发射落区约束难以调整射向，其按无偏航标准弹道飞行达到的停泊轨道倾角为28.5°，施加偏航程序后，可将倾角范围扩大至23~37°，超出这一范围的发射会消耗大量燃料用于火箭偏航，甚至出现运载能力为负值的情况，因而通常不作考虑。在28.5°时火箭可以不损失运载能力完成入轨，如要求停泊轨道倾角是23~37°，而非28.5°的值，则相较无偏航发射情况，一定会有部分的运载能力损失。

运载能力大小是深空探测任务设计的重要指标，以往在初步的轨道设计中，并未定量考虑由于弹、轨道拼接倾角问题带来的运载能力损失，在此可进行一般化定量分析。首先对该型运载火箭发射能力范围内的多点运载能力进行计算，并以发射能量为0时的标准运载能力为标准进行无量纲化处理，记该型火箭可达到的最大发射能量为3max、各点以3max为标准无量纲化算得的无量纲发射能量为3、各点算得的无量纲运载能力为m，结果见表1。

表1 不同发射能量和轨道倾角下无量纲运载能力

Tab.1 Normalized Capacity under Different Lauch Energy and OrbitalInclination

C3*无量纲运载能力m*轨道倾角23.0°轨道倾角28.5°轨道倾角37.0° 0.0000.4871.0000.630 0.1250.4000.8670.535 0.2500.3190.7430.444 0.3750.2430.6330.361 0.5000.1720.5300.284 0.6250.1050.4410.211 0.7500.0430.3540.143 0.875-0.0160.2750.081 1.000-0.0710.2070.021

利用表1数据可以插值得到一般情况，使用线性插值方法，通过周边4个点的实际无量纲运载能力数据，能得到任意发射能量和轨道倾角范围内下的无量纲运载能力m(3,)估算值：

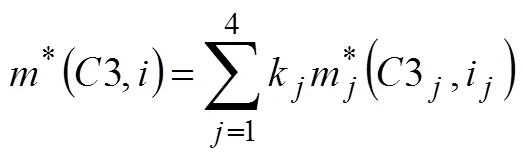
式中 kj为各项的线性插值系数。这一估值虽然不是通过真实的弹道程序运算得到，但可以反映运载能力随发射能量和轨道倾角变化的规律。为了能在同一窗口中表征不同发射能量的弹道是否损失运载能力，再利用同一发射能量下无偏航运载能力进行归一化，并通过线性插值得到所有点数据。根据同一发射能量进行归一化的无量纲运载能力插值如图4所示。

表2为发射情况与无量纲运载能力对应关系。针对不同的发射能量和出发速度角所在区间，可以确定运载火箭的发射弹道是否存在以及是否需要施加偏航，进而计算无量纲运载能力。如果窗口中的出发发射能量高于3max，则将无量纲运载能力置为-0.5，如果发射能量满足但出发速度角不在可行范围内，则将无量纲运载能力置为0，以示区分。其余部分可按插值公式计算。

表2 发射情况与无量纲运载能力对应关系

Tab.2 Correspondence between Launch Mode and Normalized Capacity

发射能量所在区间出发速度角区间发射弹道无量纲运载能力 [C3max，+∞]不考虑无法发射置为-0.5 [0，C3max][-90°,-90°+istd]无偏航发射1 (-90°+ istd，-90°+ imax]施加偏航发射插值计算 (-90°+ imax，90°-imax)无法发射置为0 [90°- imax，90°- istd)施加偏航发射插值计算 [90°- istd，90°]无偏航发射1

按照如上发射能力匹配图3中的发射窗口，发现出于火箭可达轨道倾角范围限制，无法满足其中任何一点出发要求。为了研究弹、轨道拼接问题中的轨道倾角匹配关系，可以假想将弹道能够达到的轨道倾角上限max映射至更大的数值，以此来观察max大小对发射窗口的影响。

2.3 调整偏航能力对弹轨道拼接的影响分析

将max分别映射至50°、70°、90°3个值，并利用式（4）中相同的方法插值计算，只考虑出发速度增量最小的窗口，计算图3中每一点对应的无量纲运载能力，所得结果如图5所示。

图5 不同发射轨道倾角上限对应出发窗口的无量纲运载能力

分析图5中的出发窗口变化规律可发现，max小于50°时有效发射机会很少，尽管深空轨道计算出的发射能量小于运载火箭最大能力，但是由于出发角度限制，深空轨道不满足运载火箭的出发约束。随着max逐渐增大，可以发现窗口中的浅色阴影区域随之扩大，直到max等于90°时，该窗口的全部区域都可以实现发射，但也均有不同程度的运载能力损失，这说明偏航能力大小会影响深空轨道与主动段弹道拼接的裕度。

2.4 调整射向对弹轨道拼接的影响分析

在实际运载火箭弹道设计中，无法实现在保证运载能力不变的情况下大幅增加偏航能力，因此单纯寄希望于增加偏航去覆盖0~90°内所有倾角的停泊轨道是不现实的。保持火箭偏航能力不变，单纯调整发射射向也可以达到不同轨道倾角，分别计算3类弹道，使其达到停泊轨道的倾角偏移量d为10°、30°、50°，得到图3窗口内的无量纲运载能力云图变化见图6。

图6 不同发射射向对应出发窗口的无量纲运载能力

从图6中发现，随着标准弹道对应轨道倾角的偏移量增大，同一窗口下能够实现不损失运载能力的发射窗口也相应扩张，覆盖到图3窗口中63~117°的倾角范围，这是因为大停泊轨道倾角可以适应更多的速度出发角。可以断定，当标准弹道对应的停泊轨道倾角达到90°时，在任意窗口内均可以实现不施加偏航程序的发射，这一发射弹道有利于深空探测任务。

3 结论与展望

本文对考虑发射约束的小行星探测弹、轨道拼接设计方法进行了初步分析，说明了在一般情形下的弹、轨道拼接模式，指出了现有局部优化方法的局限性。通过对地球出发至健神星小行星直接转移轨道的能量分析，得出了不同转移轨道对发射轨道倾角的约束要求，给出了可用于全局优化设计的方法，并且定性分析了运载火箭末级滑行时间对这一窗口的影响。

通过本文的研究分析，可以得到以下3点结论：

a）从深空探测任务规划全局角度来看，弹道设计和轨道设计是全段轨迹设计中的2个部分，对其进行联合优化设计具有很强的工程实际意义。

b）从弹道优化设计角度来看，本文算例中的健神星探测窗口不适合低轨道倾角发射弹道，如果能调整火箭射向以匹配停泊轨道倾角，那么高轨道倾角发射弹道可以更灵活地与深空探测任务出发轨道进行拼接，若设计适用于未来特定任务的深空探测火箭，建议其标准弹道涵盖停泊轨道倾角为90°的发射情况，以增强任务适应性。

c）从轨道优化设计角度来看，基于特定型号运载火箭进行深空发射任务，出发窗口是一个停泊轨道上多维相空间中的概念，如果只单纯限制发射能量对轨道进行优化搜索，相当于只考虑了一维约束。基于指定火箭的发射能力，提出一种联合优化设计方法，可进一步寻找满足轨道倾角约束的发射机会。

进一步展望后续工作，在弹、轨道拼接满足倾角约束后，可以考虑运载火箭末级滑行时间对窗口的影响。依照同样思路，可以通过引入滑行时间罚函数来增强对全局寻优过程的控制。

[1] 李俊峰, 宝音贺西, 蒋方华. 深空探测动力学与控制[M]. 北京: 清华大学出版社, 2014.

Li Junfeng, Baoyin Hexi, Jiang Fanghua. Dynamics and control of interplanetary flight[M]. Beijing: Tsinghua University Press, 2014.

[2] Huntress W T , Moroz V I , Shevalev I L . Lunar and planetary robotic exploration missions in the 20th century[J]. Space Science Reviews, 2003, 107(3-4): 541-649.

[3] 吴伟仁, 于登云. 深空探测发展与未来关键技术[J]. 深空探测学报, 2014, 1(1): 5-17.

Wu Weiren, Yu Dengyun. Development of deep space exploration and its future key technologies[J]. Journal of Deep Space Exploration. 2014, 1(1): 5-17.

[4] 崔平远, 乔栋, 崔祜涛. 小行星探测目标选择与转移轨道方案设计[J]. 中国科学: 技术科学, 2010, 40(6): 677-685.

Cui Pingyuan, Qiao Dong, Cui Hutao. Target selection and transfer trajectories design for exploring asteroid mission[J]. Science China Technological Sciences, 2010, 40(6): 677-685.

[5] 陈杨, 唐歌实, 李黎, 宝音贺西, 李俊峰. 第三届全国深空轨道设计竞赛总结[J]. 力学与实践, 2012, 34(2): 97-101.

Chen Yang, Tang Geshi, Li Li, Baoyin Hexi, Li Junfeng. Summary of 3rd ntional dep sace obit dsign cmpetition[J]. Mechanics in Engineering. 2012, 34(2): 97-101.

[6] 路毅, 车征, 李恒年, 黄普, 李军锋, 黄岸毅, 李济生. 第六届全国空间轨道设计竞赛(题目甲)总结[J]. 力学与实践, 2015, 37(2): 276-281.

Lu Yi, Che Zheng, Li Hengnian, Huang Pu, Li Junfeng, Huang Anyi, Li Jisheng. Summary of 6th national deep space orbit design competition(Subject A)[J]. Mechanics in Engineering, 015, 37(2): 276-281.

[7] 郗晓宁, 等. 月球探测器轨道设计[M]. 北京: 国防工业出版社, 2001.

Xi Xiaoning, et al. Orbit design of lunar probe[M]. Beijing: National Defense Industry Press, 2001.

[8] 余梦伦. 20世纪90年代大运载总体方案论证的一些回顾[J]. 宇航总体技术, 2018, 2(2): 7-16.

Yu Menglun. Review of the demonstration of general scheme of large launch vehicle in 1990s[J]. Astronautical Systems Engineering Technology, 2018, 2(2): 7-16.

Research on Ballistic-orbit Splicing in Asteroid Exploration Mission Based on Orbital Inclination Constraint

Zhang Bo-rong, Ma Ying, Zhou Tian-shuai, He Wei, Rong Yi

(Beijng Institute of Astronautical Systems Engineering, Beijing, 100076）

Ballistic optimization and orbit optimization are both required when designing a complete asteroid exploration orbital scheme. In view of insufficient consideration of terminal constraint of ballistic section and low design efficiency in current splicing design method, constraint form of designated launching trajectory to LEO is calculated based on actual ballistic calculation data. Influence of yaw ability and launching direction angle todimensionless carrying capacity are studied. Results show that detection window of Hygiea is unsuitable for loworbital inclination launch trajectory. Highorbital inclination launch trajectory can better adapt to the requirements of deep-space exploration tasks that fly out of Earth's sphere of influence. According to research results, design requirements for future deep space exploration launch vehicles are proposed.

launch vehicle; launch energy; orbit inclination; asteroid exploration; ballistic-orbitsplicing

O315

A

1004-7182(2020)01-0027-06

10.7654/j.issn.1004-7182.20200105

2017-10-13；

2018-02-23

张博戎（1991-），男，博士研究生，主要研究方向为弹轨道优化设计。

马 英（1978-），男，博士，研究员，主要研究方向为运载火箭弹道设计。

周天帅（1979-），男，高级工程师，主要研究方向为运载火箭弹道设计。

何 巍（1979-），男，博士，研究员，主要研究方向为运载火箭总体设计。

容 易（1978-），女，博士，研究员，主要研究方向为运载火箭总体设计。