直驱风电机组与SVG交互作用引发次/超同步振荡的机理与特性研究

曹 娜，管雪帅，于 群，李 琰

（1.山东科技大学 电气与自动化工程学院，山东 青岛 266590；2.中国电力科学研究院有限公司，北京100192）

0 引言

随着以风电为代表的新能源发展，直驱风电机组 （direct drive permanent magnet synchronous generator，DPMSG）因其自身的优良特性，得到了较多的应用[1]，[2]。由于风电场中的风电机组变流器、无功补偿装置等电力电子装置响应速度快、无惯性、过载能力弱、抗电网扰动能力差等限制，其控制能力对外部电网环境具有较强的依赖性[3]。因此，风电机组与无功补偿装置之间的运行控制相互耦合和影响，有可能诱发并加剧风电机组发生次/超同步振荡的风险。

针对直驱风电场接入弱交流系统出现的次/超同步振荡现象，文献[4]基于小扰动的导纳分析法，建立了直驱风机端口输入导纳模型。文献[5]利用正、负序阻抗建模方法，研究直驱风电机组并网产生次同步振荡的机理，并提出了一种锁相环优化方法。文献[6]在考虑锁相环和解耦控制环节的基础上，采用小信号方法，对直驱风机汇集母线存在的多个次/超同步频率分量现象给出理论解释。文献[7]通过推导直驱风电机组网侧变流器（grid side converter，GSC）控制环节与电网之间谐波的响应过程，分析了次/超同步振荡的引发机理并给出了稳定性判据。上述研究多基于直驱风电并网对电力系统稳定性的影响，缺乏对无功补偿装置与直驱风电机组的运行控制相互耦合作用的认识。

本文根据直驱风电机组网侧变流器与静止无功发生器（static VAR generators，SVG）的电路拓扑及控制策略，利用谐波线性化方法，建立了直驱风电机组与SVG交互作用的正序阻抗模型，并给出了基于阻抗的稳定性判据。在此模型基础上，利用波特图分析SVG控制参数对直驱风电机组的影响，揭示锁相环和电流环控制参数对直驱风电机组与静止无功发生器交互作用的次/超同步振荡特性的作用规律。最后，在Matlab/Simulink中搭建直驱风电机组并网系统模型进行时域仿真，并与频域分析结果比较，验证了阻抗特性分析的合理性。

1 直驱风电机组和SVG正序阻抗模型

风电场中包含n台同型号的1.5 MW直驱风电机组，它们连接于同一条母线上，且控制参数与运行状态一致。风电场发出的电能经升压变压器接入110 kV交流主网，场内安装有无功补偿装置SVG。

利用对称分量法并结合谐波线性化方法，将系统分解成正、负序两个子系统，对于三相平衡的对称系统而言，不存在负序分量。本文在平衡工况下建立直驱风电机组和SVG正序阻抗模型，主要考虑二者的电路结构、控制策略对阻抗特性的影响。

图1为电网电压定向控制的GSC基本电路及控制策略。图中：Uwdc为直流侧电压；Lw为滤波电感；Cw为直流侧电容；Cfw为滤波电容；Rfw为阻尼电阻；uwa，uwb，uwc为 GSC 输出电压；ua，ub，uc和iwa，iwb，iwc分别为GSC的公共并网点（point of common coupling，PCC）三相电压和电流；Zg为电网电抗；uga，ugb，ugc为交流电网三相电压；Hwi（s）为GSC的电流调节器传递函数；Gwi（s）为电流采样延时环节等效传递函数；Kwdq为GSC的交叉解耦系数。

图1 直驱风电机组网侧变流器主电路拓扑Fig.1 The main circuit topology of grid-side converter in full-scale power converter turbine

图2为SVG基本电路及控制策略。图中：Usdc为直流侧电压；Ls为滤波电感；Cs为直流侧电容；usa，usb，usc为 SVG 输出电压；ua，ub，uc和 isa，isb，isc分别为SVG的公共并网点三相电压和电流；Hsi（s）为SVG的电流调节器传递函数；Gsi（s）为电流采样延时环节等效传递函数；Ksdq为SVG的交叉解耦系数。

图2 SVG主电路拓扑Fig.2 The main circuit topology of SVG

1.1 直驱风电机组和SVG锁相环谐波线性化

直驱风电机组GSC和SVG采用同步静止坐标系锁相环 （synchronous reference frame phase locked loop，SRF-PLL），两个锁相环中的传递函数HwPLL（s）和 HsPLL（s）分别为

式中：kwp，kwi和 ksp，ksi分别为直驱风电机组 GSC和SVG的锁相环比例系数与积分系数。

对直驱风电机组的PLL进行频率特性分析。根据谐波线性化方法，假设特定频率的正序电压谐波分量存在于公共并网点，PLL通过对PCC电压锁相，得出dq轴坐标系坐标变换角度θ。假设 θ=θ1+Δθw，其中，θ1为正序基频电压产生的稳态同步并网相角，Δθw为正序电压谐波产生的扰动相角，得到与 Δθw之间的传递函数为[8]

1.2 直驱风电机组与SVG正序阻抗模型

图1中，直驱风电机组输出电压、电流和PCC处电压之间的关系为

直驱风机并网电流经坐标变换和傅里叶变换得到其频域表达。在通过电流调节器后，得到dq轴电压指令值，然后分别经过以θ1和θ为旋转角的帕克反变换转换到abc坐标下，得到不考虑PLL和考虑PLL的直驱风电机组输出电压的频域表达式。结合并网点电流和并网点电压的频域表达，并带入式（7）中，可分别推得不含锁相环和含锁相环的直驱风机GSC正序阻抗模型为[8]

式中：kwip，kwii分别为直驱风电机组GSC电流调节器比例系数、积分系数；Kwdq为GSC的交叉解耦系数；Gwi（s）为电流采样延时环节等效传递函数[5]；D=1/2Dw±j1/2Qw，其中 Dw，Qw分别为直驱风电机组电流调节器 d，q 轴的直流输出量[8]；Gwu（s）为电压采样延时环节等效传递函数[5]；Iw1为基波电流幅值。

同理，根据图2中SVG输出电压、补偿电流和PCC处电压关系，也可得到不考虑PLL和考虑PLL两种情况的SVG阻抗模型，分别如式（10），（11）所示。

式中：ksip，ksii分别为SVG电流调节器比例系数、积分系数；Ksdq为 SVG 交叉解耦系数；Gsi（s）为电流采样延时环节等效传递函数；D′=1/2Ds±j1/2Qs，其中Ds，Qs分别为 SVG电流调节器 d，q轴直流输出量；Gsu（s）为电压采样延时环节等效传递函数。

2 直驱风电机组与SVG交互的正序阻抗模型

2.1 不考虑PLL的交互阻抗模型

不考虑锁相环的影响，由式（8），（10）可得不含锁相环的二者交互的正序阻抗模型为

2.2 考虑PLL的交互阻抗模型

考虑锁相环的影响，由式（9），（11）可得含有锁相环的二者交互的正序阻抗模型为

式中：Bp1和Bp2分别为直驱风电机组和SVG锁相环参数与基频电流、静态工作点和电流环控制参数耦合环节。

2.3 稳定性判据

电网与风电机组之间的稳定性可由级联系统稳定性判据[9]进行判断。图3所示为其等效阻抗网络，ib和ug分别为理想电流源和理想电压源。

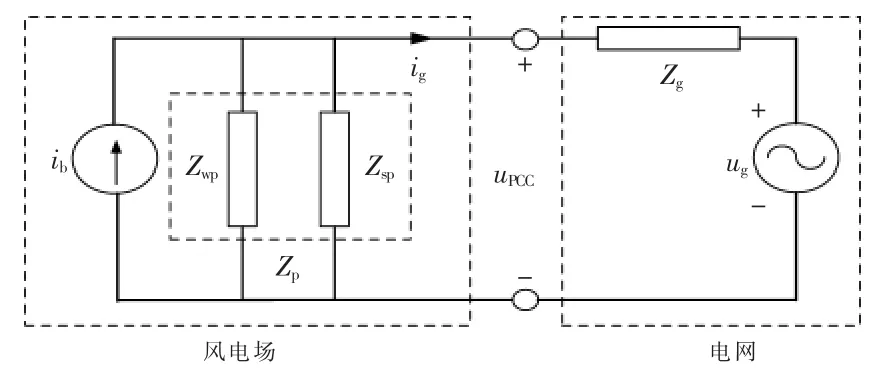
图3 直驱风电机组并网系统正序等效阻抗网络Fig.3 The positive equivalent impedance model of DPMSGs integrated in a grid

由式（15）可知，直驱风电并网系统稳定须满足两个条件：①1/Zp（s）稳定；②在电网阻抗一定的情况下，保证 Zg（s）/Zp（s）满足奈奎斯特稳定性判据。由式（14）可知，控制参数的变化会引起输出阻抗幅值和相位的变化和波动。因此，在输出阻抗幅值变化的绝对值增大、相位波动性较大的频段，如果不满足上述稳定条件，系统发生振荡的风险就会增大。

3 直驱风电机组模型验证及阻抗特性分析

为了验证上述分析建模的合理性，在Matlab平台上建模。在分析过程中，将6台直驱风电机组组成的风电场等值成一台容量为9 MW的风电机组，其主要电气及控制参数如表1所示。SVG的补偿容量为±1 Mvar，参数如表2所示。锁相环和电流环控制参数对系统运行特性的影响将直观地体现于并网电流中。

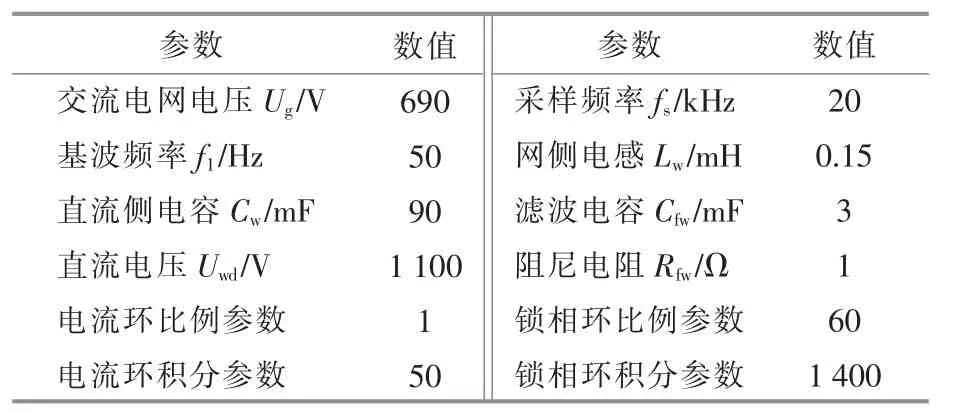
表1 直驱风电机组网侧变流器参数Table 1 Parameters of a grid-side converter in full-scale power converter turbine

表2 静止无功发生器参数Table 2 Parameters of a static var generator

3.1 SVG和锁相环对输出阻抗特性的影响

图4为输出阻抗特性曲线，通过对比Zwp和Zp可知，SVG投入后输出阻抗幅值变小，这种阻抗的变化说明了SVG与直驱风电机组相互控制耦合，共同作用于系统的输出阻抗。此外，由曲线Zp和Z可知，考虑锁相环相对不考虑锁相环时的输出阻抗幅值变小。这是由于在考虑锁相环后，阻抗模型的分母多出了两项表达式者共同作用于阻抗模型的分母中，使得考虑锁相环时的输出阻抗减小，系统受扰后易出现不稳定的状态。

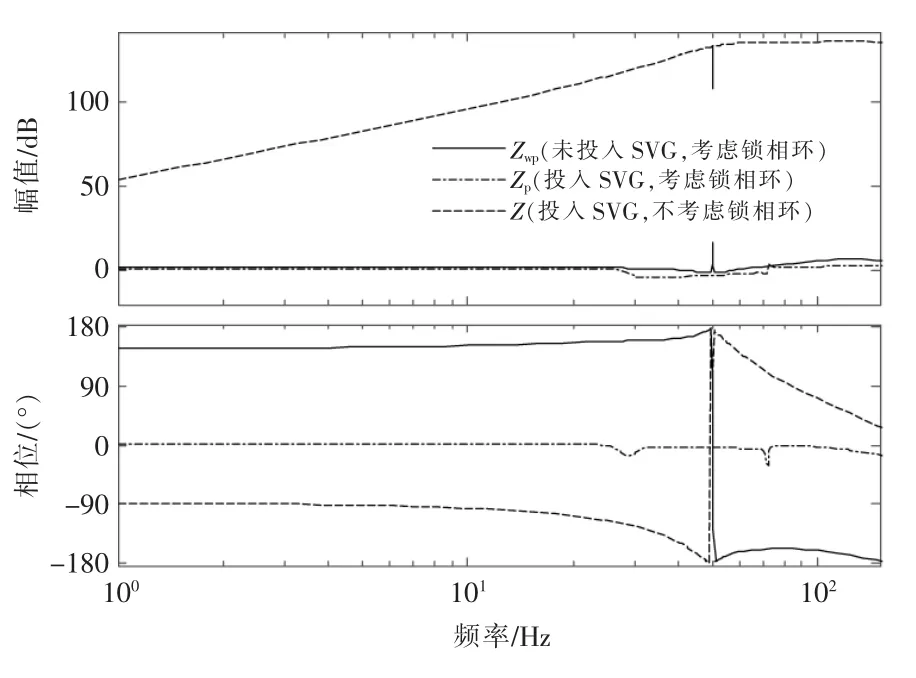
图4 SVG投入前后输出阻抗波特图Fig.4 Bode diagram of output impedance before and after the input of SVG

3.2 直驱并网系统阻抗特性分析及仿真验证

3.2.1 锁相环控制参数影响分析

通过阻抗模型（14）可知，锁相环控制参数影响着直驱并网系统的输出阻抗特性。图5给出了3种情况下的输出阻抗特性曲线：a-直驱风电机组控制参数正常 （kwp=60，kwi=1 400）；b-直驱风电机组锁相环控制参数取值较小（kwp=0.1，kwi=150）；c-直驱风电机组锁相环控制参数取值较小的前提下，投入锁相环控制参数取值较小的SVG（kwp=0.1，kwi=150，ksp=0.1，ksi=150）。

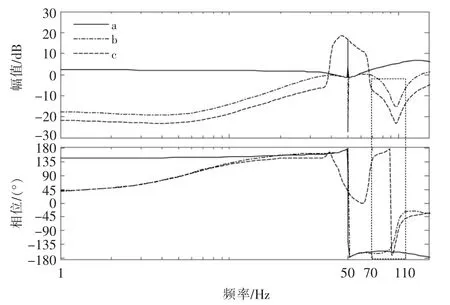
图5 输出阻抗波特图Fig.5 Bode diagram of output impedance

由图可知，b，c两种条件下的输出阻抗幅值在70～110 Hz减小的绝对值增大，相位出现较大波动性，由阻抗稳定性判据可知，相应频段系统发生振荡的风险增大。

为了验证图5中阻抗特性分析的正确性，本文对不同条件下直驱风电机组A相电流输出波形和频谱进行了分析，结果如图6所示。

图6 不同条件下直驱风电机组A相电流输出波形和频谱分析Fig.6 The current waveforms of a DPMSG with different situation and FFT analysis

由图 6（a）可知，在 b，c 两种情况下，直驱风电机组输出电流波形均出现了振荡现象。由图6（b）可以看出：a条件下，系统中无次/超同步振荡分量，处于稳定运行状态；b条件下，系统中超同步频率分量的含量较大，以90 Hz附近分量为主；c条件下，系统中90 Hz附近分量增加。

直驱风电机组锁相环控制参数的取值主要影响超同步频段，且当SVG的锁相环控制参数取值较小时，会加剧超同步振荡的风险。

3.2.2 电流环控制参数影响分析

图7 输出阻抗波特图Fig.7 Bode diagram of output impedance

电流环控制参数的取值也影响着输出阻抗特性。图7所示为3种条件下的输出阻抗特性曲线：d-直驱风电机组控制参数正常（kwip=1，kwii=50）；e-直驱风电机组电流环比例参数取值较小 （kwip=0.01，kwii=50）；f-直驱风电机组电流环比例参数取值较小的前提下，投入电流环比例参数取值较小的 SVG（kwip=0.01，kwii=50，ksip=0.08，ksii=200）。

由图7可知，e，f两种条件下输出阻抗幅值在20～30 Hz和80 Hz附近减小的绝对值增大，相位出现较大波动性，由阻抗稳定性判据可知，相应频段系统发生振荡的风险增大。图8为不同条件下直驱风电机组A相电流输出波形和频谱分析。

图8 不同条件下直驱风电机组A相电流输出波形和频谱分析Fig.8 The current waveforms of a DPMSG with different situation and FFT analysis

由图 8（a）可知，e，f两种条件下并网电流输出波形均出现了一定程度的振荡。由图8（b）可知，e条件下系统中出现了30 Hz和80 Hz附近分量。在此前提下，f条件下系统中30 Hz和80 Hz附近分量的含量则会增大。

直驱风电机组电流环比例参数的取值对次/超同步频段都有影响，且投入的SVG电流环比例参数取值较小时，会加剧振荡。相对于锁相环控制参数的取值对系统稳定性造成的影响，电流环比例参数取值的影响要更小一些。

4 结论

本文推导了含锁相环的直驱风电机组与SVG交互作用的正序阻抗模型，研究了二者交互作用引起的次/超同步振荡问题，得出以下结论。

①SVG的投入减少了直驱风电机组的输出阻抗，二者控制参数相互耦合，共同影响着并网系统的输出阻抗特性。

②直驱并网系统锁相环和电流环控制参数对其输出阻抗特性有着不同程度的影响，这些参数设置不当，会激发系统振荡的风险。直驱风电机组锁相环控制参数的取值主要影响超同步频段，当SVG的锁相环控制参数设置不当时，会加剧系统超同步振荡的风险。直驱风电机组电流环比例参数的取值对次/超同步频段都有影响，当投入的SVG电流环比例参数设置不当时，会加剧系统振荡。