轮式移动机器人全局轨迹跟踪控制

赵 涛，王屹华

(西北机电工程研究所，陕西 咸阳 712099)

0 引 言

随着机器人技术的发展，轮式移动机器人的轨迹跟踪控制问题越来越受到了人们的关注。长期以来，大量学者从事这方面的研究工作。文献[1]采用Lyapunov 重设计方法设计修正项, 使得闭环系统对滑动干扰鲁棒。文献[2]由移动机器人在极坐标系中的运动学方程出发设计一个滑模控制器, 进而提出了一种新的滑模控制方法, 解决了在极坐标系中关于运动学的跟踪问题。文献[3]利用反演技术和积分滑模控制的思想设计了自适应滑模控制器，该控制器能有效地克服未知扰动的影响。文献[4]从轮式移动机器人的运动学特性出发， 根据轮式移动机器人误差的状况， 提出多模态控制和模糊控制相结合的控制方法。文献[5]运用Lyapunov 方法和自适应技术设计了一种自适应统一控制器, 该控制器可以保证跟踪误差全局一致最终有界。文献[6]结合Backstepping 方法设计了基于移动机器人运动学模型的轨迹跟踪控制律, 并给出了参数选取条件。文献[7]提出了一种改进的非线性反推跟踪控制算法，并引入了一个反馈控制律。然而，文献[1-7]可以看出，设计控制器的过程都相当的复杂。

根据轮式移动机器人的运动学模型，通过设计复合跟踪误差，采用级联方法进行轨迹跟踪控制器设计，轮式移动机器人的位置跟踪和航向角跟踪分解为级联系统的形式，基于反演设计方法，通过设计前向推力的控制律，使位置跟踪误差全局一致渐近稳定，同时可以容易地获得航向角跟踪误差的全局指数稳定控制律，从而证明了轨迹跟踪误差的全局渐近稳定性。仿真结果表明，该算法轨迹跟踪效果良好，满足轮式移动机器人的轨迹跟踪控制要求。

1 问题描述

本文研究对象为二自由度轮式移动机器人，当不考虑车轮滑动时，其动力学特性由如下微分方程描述：

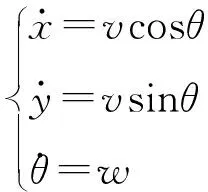
(1)

式中，x、y分别为轮式移动机器人的笛卡尔坐标，θ为轮式移动机器人的航向角，v和w分别为平移速度和转动速度，在运动模型中它们是控制输入。

考虑轮式移动机器人的轨迹跟踪控制时，跟踪控制系统可以用如下方程描述 ：

(2)

式中，vr和wr分别为预定轨迹的参考平移速度和参考转动速度，位置和航向跟踪误差向量(xeyeθe)定义为

(3)

式中：(xryrθr)T为轮式移动机器人的参考位姿指令。图1为轮式移动机器人的误差坐标系。

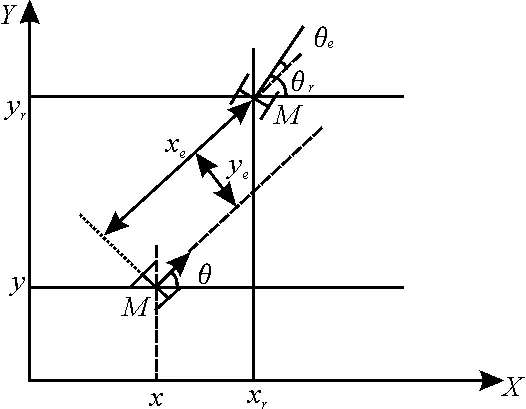
图1 轮式移动机器人的误差坐标系

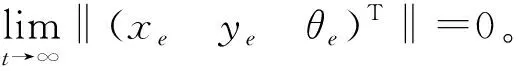
2 控制器的设计

轨迹跟踪误差写作级联形式：

(4)

(5)

采用级联-反演方法设计控制器：

第一步：

定义Lyapunov函数V1为

(6)

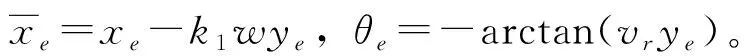
其导数为

(7)

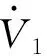
(8)

则有

(9)

根据辅助定理：对于任意x∈R和|x|<∞, 总是存在φ(x)=xsin(arctan(x))≥0。当且仅当x=0时, 方程等号成立。可知，

(10)

第二步：

定义Lyapunov函数V2为

(11)

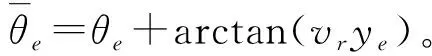
其导数为

(12)

其中，取α=-arctan(vrye)。

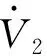
(13)

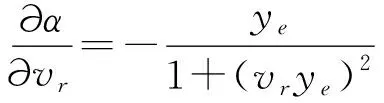
对式(13)，求导则有

(14)

根据式(6)至式(14)，证明了轨迹跟踪误差的全局渐近稳定性。

3 仿真研究

为了验证上述控制算法的控制性能，在Matlab仿真环境下，对轮式移动机器人进行了直线运动和圆周运动跟踪控制。

跟踪参考轨迹为平移速度和转动速度为匀速运动的圆轨迹。位姿误差初始值[3 0 0]。控制参数取为k1=k2=k3=6。参考速度指令vr=wr=1。

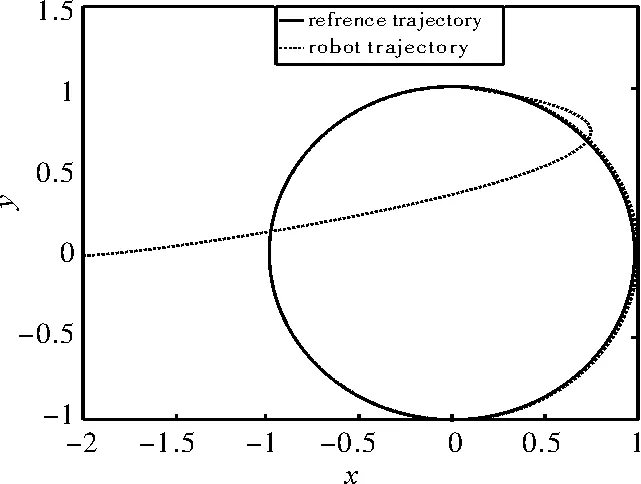
图2 圆轨迹跟踪仿真图

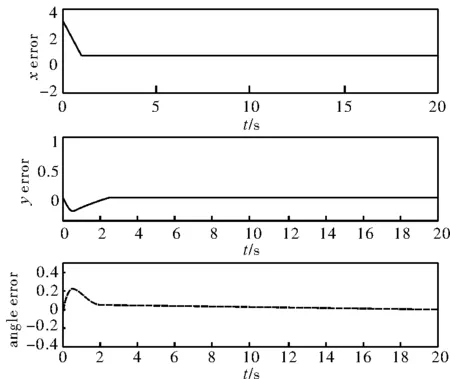
图3 跟踪误差仿真图

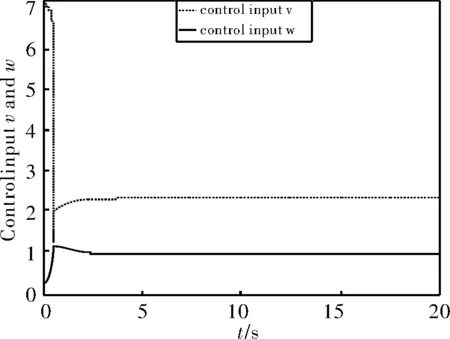
图4 控制输入仿真图

从仿真图2～图3可看出，系统在不到2s的时间内即进入稳态，在所设计的控制器的作用下，跟踪误差快速的收敛到零，具有良好的跟踪性能，且控制输入(vw)T全局有界，满足轮式移动机器人轨迹跟踪控制要求。

4 结 语

基于级联系统理论为轮式移动机器人设计了性能良好的轨迹跟踪控制律，在分析系统稳定性的基础上，保证了控制系统的全局稳定性。仿真结果表明，初始跟踪误差很快收敛于零，闭环系统具有良好的动态性能、轨迹跟踪效果和全局稳定性，适用于轮式移动机器人的全局轨迹跟踪控制。