一种基于残差矢量的六相逆变器故障诊断策略

孙晟桐，刘 剑，宋吉江，赵 博，王新维，谭芳堃

(山东理工大学 电气与电子工程学院，山东 淄博 255000)

0 引 言

六相永磁同步电机具有低压大功率、效率高、可容错、噪声低等性能优点，已被应用于舰船推进、航空推动器等高可靠要求较高的应用场合，国内外学者在六相永磁同步电机的故障后的容错控制已有较多的研究，但目前根据六相永磁同步电机的故障信息如何进行故障诊断的研究还很少。对六相电机或多相逆变器的功率器件进行故障的准确定位和故障诊断是进行容错控制的前提，是提高六相永磁同步电机逆变器可靠性的关键[1-4]。

六相永磁同步电机逆变器开路故障诊断策略可大致分为以电流信息为诊断依据和以电压信息为诊断依据两大类[5-6]。与基于电压变量的故障诊断策略相比，电流变量的获取可避免使用额外的电压传感器，以此达到降低诊断策略的复杂性和诊断成本的目的。因此本文对基于电流信息的故障诊断策略进行研究。

国内外学者的研究多针对多相永磁同步电机逆变器开路故障诊断技术。法国里尔中央理工大学的Moraes T.J.D.S结合空间矢量理论，对六相定子电流按照两套绕组的基波平面电流分量的特性进行研究，仿真验证了基于此的开路故障诊断方法[7]。沈阳工业大学的姜俊使用小波包对定子电流特征进行提取，并基于流形理论进行了优化，同时使用支持向量机对故障样本进行了训练，最后得到故障诊断模型[8]。瑞士联邦工学院Morari博士等为解决一些复杂混合系统的分析、设计等问题提出混合逻辑动态模型[9]。美国德克萨斯农工大学的Niloofar Torabi基于机器学习技术，提出了一种多相永磁同步电机开路故障隔离的故障诊断策略[10]。该方法特点在于将基于组件和基于系统的故障诊断方法相结合，构建了基于组件的信号为输入，而以系统为基础的信号为输出的故障诊断混杂模型。

上述的基于电流信息的故障诊断策略均存在诊断周期长、鲁棒性较低等问题，所以本文将提出一种降低诊断周期、提高诊断策略可靠性的六相永磁同步电机驱动系统逆变器开路故障诊断策略。

本文提出了基于混合逻辑动态模型的逆变器开路故障诊断策略。首先基于六相永磁同步电机驱动系统逆变器建立混合逻辑动态模型，然后将开关管故障时混合逻辑动态模型产生的电流值与电机驱动系统产生的电流值作差，获得包含故障角与幅值的残差矢量，以进行故障诊断与定位。同时为提高诊断策略的鲁棒性，提出了阈值电流判定法。最后，在Matlab/Simulink中对所提的诊断策略进行了仿真，验证了该方法的准确性与有效性。

1 六相永磁同步电机驱动系统混合逻辑动态模型

1.1 六相永磁同步电机电流数学模型

图1 六相永磁同步电机驱动系统示意图

由图1知，六相静止坐标系下的永磁同步电机电压数学模型如下：

(1)

ψk=Lkik+ψfFk(θe)

(2)

式中,ukn为定子相电压矩阵，ik为定子电流矩阵，ψk为定子磁链矩阵，Rk为定子电阻矩阵，Lk为定子电感矩阵，θe为转子纵轴与A相轴线的夹角，Fk(θe)为系数矩阵，Fk(θe)表达式如下：

(3)

由式(1)～式(3)可得下式：

(4)

式中,ek为定子反电动势矩阵，表达式如下：

(5)

式中,ωe为转子电角速度，ψf为永磁体磁链。

结合图1，由基尔霍夫第二定律可得下式：

ukn=ukg-ung

(6)

此处规定两套三相绕组均为星型连接，则根据式(4)和式(5)得到下式：

(7)

结合式(6)、式(7)得到ung的表达式：

(8)

由式(4)、式(6)和式(8)可得定子电流矩阵表达式：

(9)

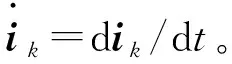
1.2 驱动系统混合逻辑动态模型

用离散开关信号s1-s12表示IGBT的导通和关断：当sj=1时，表示第j个IGBT处于导通状态；当sj=0时，表示第j个IGBT处于关断状态。同时引入表示定子电流方向的参数δk：当δk=1时，表示ik的方向为流入绕组方向；当δk=0时，表示ik的方向为流出绕组方向。此时驱动系统便成为一个由离散变量构成的混合逻辑动态模型。根据逆变器的拓扑结构，便可利用sk和δk来表示ukg，以电压uag为例，表达式如下：

(10)

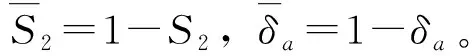
同理，电压ubg-ufg的混合逻辑表达式如下：

(11)

联立式(9)、式(10)和式(11)，得：

(12)

为方便表达，引入参数矩阵η，令

(13)

在等幅值变换原则下，结合式(13)，对式(12)进行Clark变换得：

(14)

式(14)即为六相永磁同步电机驱动系统基于混合逻辑的动态电流模型。

2 基于动态电流模型的故障诊断策略

2.1 故障电流残差法的原理

基于混合逻辑动态模型，构造驱动系统的状态估计器。当出现故障事件,即参数η发生改变时，系统的演化轨迹将发生变化,导致其状态与正常时相比出现偏差。将包含参数η的状态估计值与电机输出的实际值作差，便可诊断逆变器开关管开路故障。

为简化式(14),令

(15)

结合式(14)、式(15)对式(14)求微分得：

(16)

式(16)即为α-β轴、z1-z2轴电流的状态估计器。

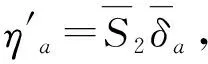
(17)

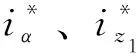
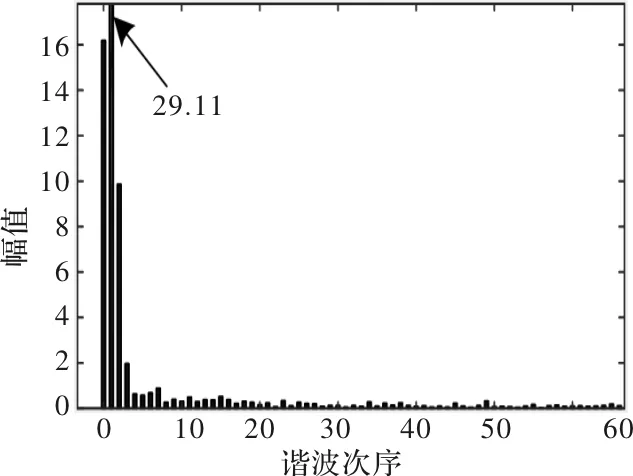
图2 s1发生开路故障后电流的谐波幅值图

此时将故障状态下的混合逻辑电流i*与正常状态下的电机电流i作差，便可得到开关管s1故障状态下的电流残差。故障状态下的混合逻辑电流i*与正常状态下的电机电流i作差结果如式(18)所示。

(18)

同理，当开关管s2发生故障，即s2=0时，此时电流残差便可写为如下形式：

(19)

当a相桥臂上下开关管s1、s2均出现故障，即s1=s2=0时，式(20)便为此时的电流残差：

(20)

式(18)、式(19)和式(20)为a相桥臂开关管发生故障的电流残差情况，剩余五相桥臂的开关管发生故障时的详细计算步骤不再陈列，对应电流残差大小分布如表1所示。

表1 故障开关管与电流残差关系图

2.2 电流残差矢量与故障定位

(21)

(22)

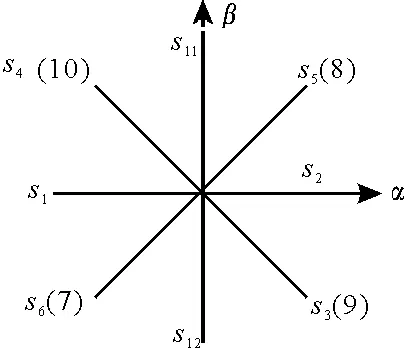
图3 α-β轴电流残差矢量图

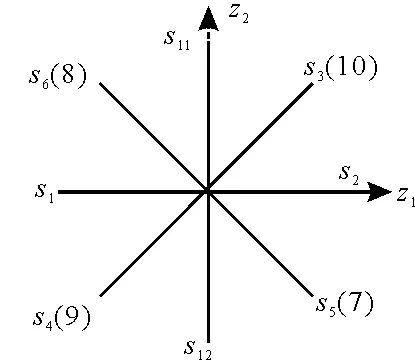
图4 z1z2轴电流残差矢量图

故障相诊断过程如下：当θαβ分别等于0°、90°、180°和270°时，此时故障开关分别为s2、s11、s1和s12。当θαβ位于4个象限内时，需同时考虑θz1z2。以开关管s5和s8为例：若θαβ位于第一象限，此时仅根据图3无法判断开关管s5和s8哪一个为故障开关，则需再根据θz1z2进行判断，若此时θz1z2位于第四象限，则表示故障开关管为s5；若此时θz1z2位于第二象限，则表示故障开关管为s8。除第一、第六相以外，其他相故障开关管的定位步骤与之相似，详细步骤如图5所示。

2.3 增加故障诊断策略的可靠性

图3、图4中的电流残差矢量为理想条件下的残差，而在实际条件下，为了增加诊断策略的可靠性，需采取以下措施：①以额定电流值为半径，以原点为圆心在图3、图4中作一个圆，以起到设定阈值的作用，解决非故障情况下电流残差矢量仍存在的问题。阈值取额定电流，根据电机参数，得到额定电流为5A。②分别将图3、图4平均划分为八个扇区，解决故障情况下残差矢量偏移故障相对应轴的问题。如图6、图7所示。

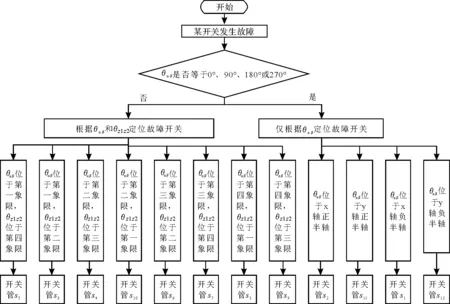
图5 故障开关定位步骤图

图6 α-β轴电流残差矢量扇区图

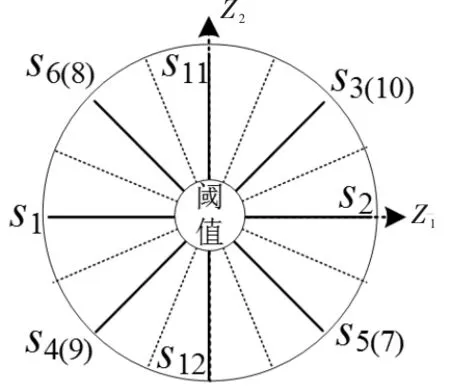
图7 z1z2轴电流残差矢量扇区图

3 实验仿真

为验证本文提出的故障诊断策略，利用Matlab/Simulink平台，搭建了转速电流双闭环的六相永磁同步电机驱动系统，并建立了基于混合逻辑动态模型的逆变器开路故障诊断模型。电机参数如表2所示。

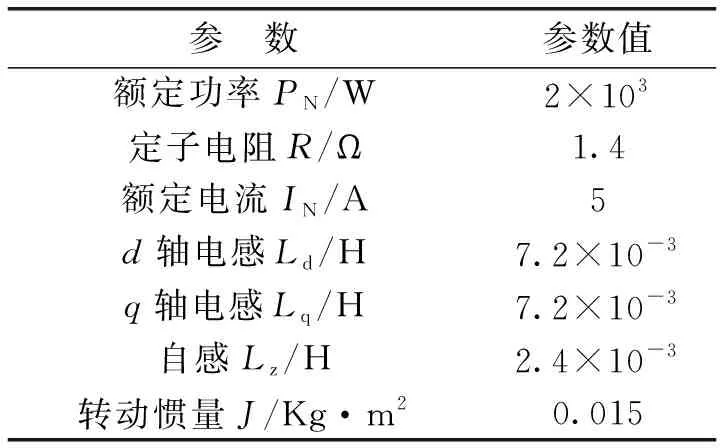
表2 电机参数

在逆变器无故障的条件下对电机增加7N·m的负荷，观察无故障的电机在增加负荷时电流残差是否会超过阈值，仿真结果如图8所示。

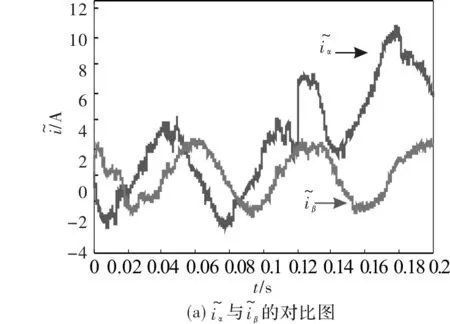
逆变器在0.12s时发生开关开路故障。图9至图11列出了开关管s1、s2发生开路故障的仿真结果。

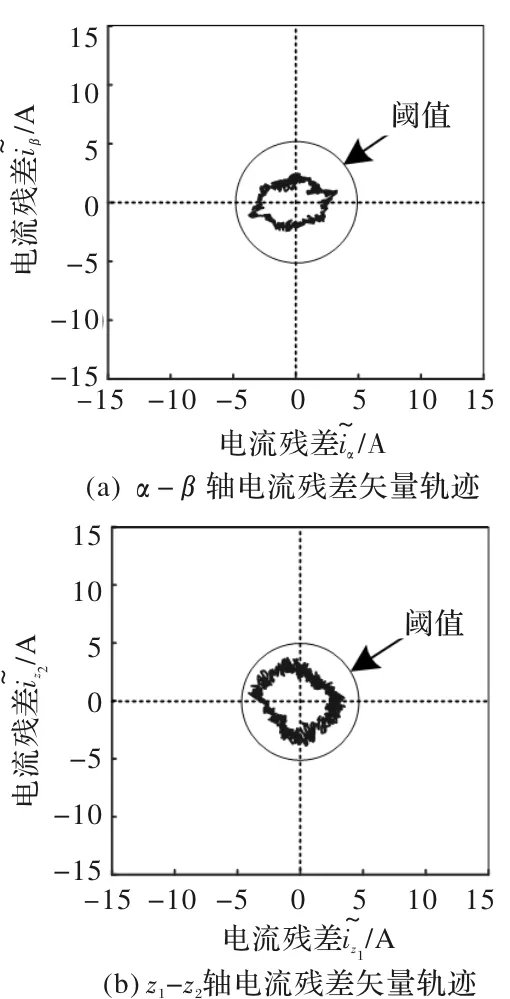
图8 无开路故障时电机增加7N·m负荷的电流残差矢量轨迹

仿真结果显示，逆变器无开路故障时，电机为7N·m负荷，电流残差矢量尽管不等于零但不会超过阈值，验证了诊断策略的鲁棒性。

图9 s1发生开路故障时的仿真图

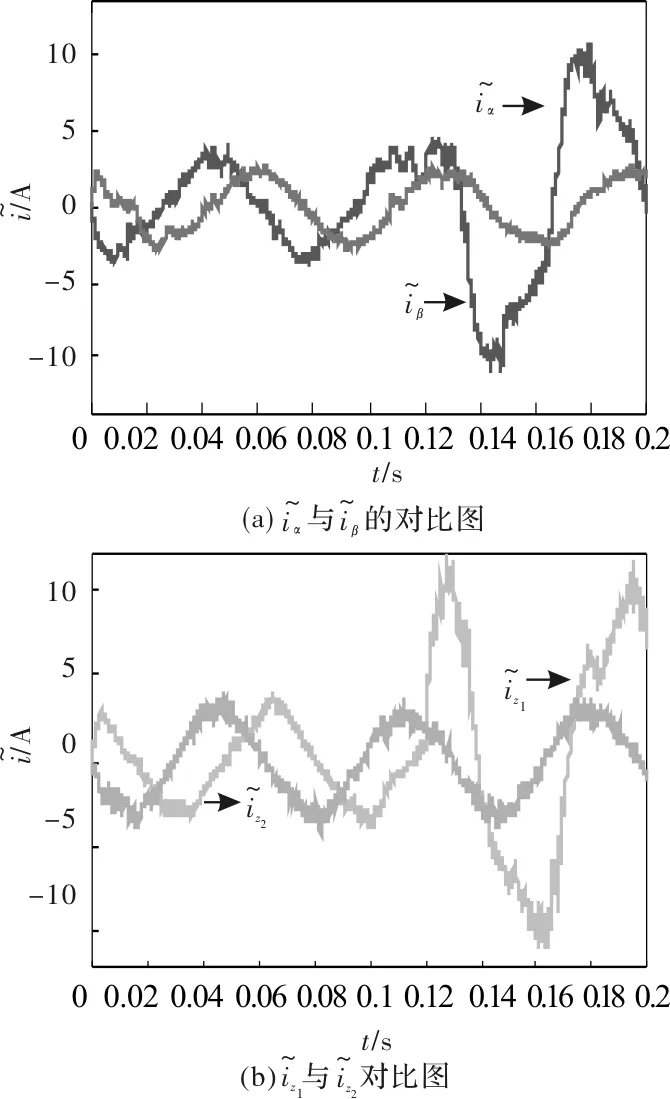
4 结 论

本文针对六相永磁同步电机驱动系统逆变器出现开路故障时单相电流发生的变化，提出了基于混合逻辑动态模型，构建电流残差矢量的故障诊断策略。与其他基于电流分量的诊断策略相比，该诊断策略具有以下优势：①将故障诊断周期降至四分之一个基波周期。②消除了系统闭环控制算法带来的影响，降低了系统的复杂度，增加了诊断策略的鲁棒性。③无需使用传感器，减少了诊断策略的成本，克服了传感器适应性低的问题。④单一开关管开路故障与上下桥臂同时发生开路故障均可被定位。