多轴电传操纵系统非线性机构与自适应控制分析

邓 俊，钟伦超

(1.四川科技职工大学，成都 610101；2.清华大学 深圳国际研究生院，广东 深圳 518000)

0 引 言

电传操纵系统(Fly by Wire，简称FBW)是控制无人直升机(Unmanned Helicopter)桨叶偏转的关键部件，其性能的好坏直接影响着无人直升机的性能和飞行安全[1-2]，电传操纵系统介于发动机齿轮箱输出到最终桨叶之间，是执行飞行控制系统的伺服、传动与控制机构。电传操纵系统接收来自飞控舵面控制指令，然后经过传动结构来控制旋翼的舵面偏角，以达到控制无人机稳定飞行和完成轨迹规划任务的目的。电传操纵系统相比于传统的机械操纵系统，省去了复杂的连杆机构，不仅重量轻，而且响应速度快[3]，更容易模块化集成，模块化更换，能够有效减小外场作业时间，提高作业效率，降低维护费用[4-5]。电传操纵系统除了确保沿整个包线飞行、操纵品质优良和均匀外，它还提供输入监测、提供警告和闭环反馈等功能，从而大大提高飞机的安全，实现关键目标“无忧无虑的操纵”[6]。

目前双旋翼直升机主要以机械传动为主，因此存在结构复杂、重量大、机械故障率高等缺点。目前所知使用同类技术及开展预研的国外机型仅有俄罗斯新一代直升机技术验证机卡92和美国X2直升机[7-8]。本文针对所研制的小型通用无人直升机，采取非线性自适应技术，对机械结构线性化处理，并在无人直升机上做了实际飞行测试。

1 机构坐标解算与模型分析

无人直升机操纵包括总距、俯仰、滚转和航向4个通道的操纵指令，即[uc,ue,ua,ur]T。所有的操纵指令都是提高舵机的控制输出执行，即对舵杆的伸缩量[l1,l2,l3,l4,l5,l6]T进行综合解算与控制，由操纵结构的运动学对应为上、下旋翼的桨距角[θu,θl]，然后采取旋翼动力学输出三轴力与力矩，进而改变无人直升机的姿态和位置。在对FBW的控制器进行设计前，需要对操纵机构进行运动学分析，操纵机构运动学建模是控制分解的理论依据。

本节采取逆运动[9]将非线性的操纵系统部分线性化，对系统位置进行正逆向的运动学分析[10]，从而建立整个系统的运动学模型。

1.1 坐标解算

上下层各自的操纵机构坐标解算如图1所示，坐标系O0x0y0z0分别与上下三个舵机传动输出轴连接，零点处于主轴的中心，将分别位于φ=0°，120°，240°的3个舵机编为U1～U3号，倾斜盘与舵机拉杆连接处为Ci(i=1,2,3)，设方位角φ沿O0x0轴负方向为0°。

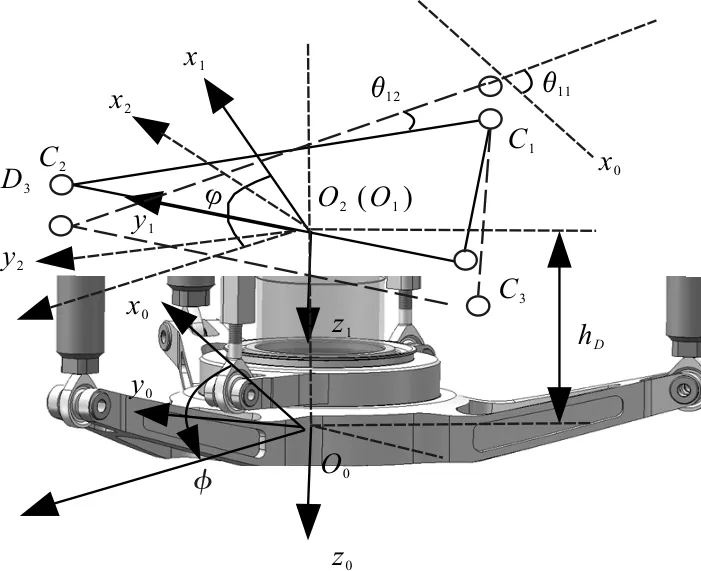
图1 操纵机构坐标表示

因为倾斜盘外环绕内环旋转，因此在不同方位角处桨距是不同的，就需要用不同位置处的倾斜角φ来表示倾斜盘的空间指向。如图1所示，实线为舵机初始位置，虚线为运动后的位置，运动后的坐标系O2x2y2z2原点位于倾斜盘中心，O2z2沿主轴向下，O2x2指向倾斜盘外环上的点D3在x2O2y2平面内进行的投影。该坐标系是动坐标系，会随着外环绕O2z2轴旋转而旋转，x2O2z2平面与倾斜盘的交叉线为O2D3，其与O2x2的夹角即为倾斜盘在该方位处的倾斜角φ(φ)，O2D3在O2x2上方时φ为正。

沿O1z1，O2x2，O2y2，O2z2的单位矢量k1，i2，j2，k2和在O0x0y0z0坐标系中表示为

(1)

(2)

(3)

(4)

由于k1与j2正交，同时O2D3为两平面交线，因此可得沿该方向的某矢量：

(5)

进一步可求得rt与和i2之间的夹角为

(6)

为求逆模型，设在倾斜盘内的两个单位矢量rt1和rt2，沿x2O2z2平面和y2O2z2平面各自与倾斜盘的交线，分别对应的角度为φf=φ和φf=φ-90°。假设已知这两处方位角倾斜盘的倾斜角分别为φ、φ′。倾斜盘单位法向量k1在O0x0y0z0中表示为

(7)

结合式(1)可得：

δx=arctan(cosφcosφsinφ′-sinφsinφcosφ′)

(8)

δy=arcsin[(-cosφsinφcosφ′-sinφcosφsinφ′)/cosδx]

(9)

1.2 模型分析

图2为上层操纵机构运动模型简化示意图(下层操纵机构运动模型类似)，设定逆时针为正(俯视)3个舵机拉杆伸缩长度分别为li(i=1,2,3，以舵机初始化找中后的初始平面为基准)，倾斜盘内环半径为d2，舵机拉杆与主轴中心距离为d3。坐标系O1x1y1z1与倾斜盘刚性连接，平面与倾斜盘同面，O1x1轴负向指向C1。上层操纵机构直接倾斜盘带动连杆，连杆带动桨毂，桨毂带动桨叶；下层操纵机构计算的2个变距通过2根变向杆连接关节轴承，关节轴承带动主轴内的两根拉杆调节上桨毂的偏转，桨毂带动桨叶。

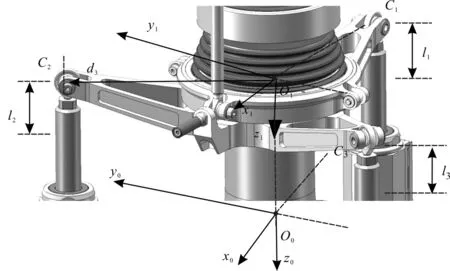
图2 操纵结构运动模型示意图

(10)

根据上式，参考文献[11]，可以进一步得到正、逆运动学模型，最终求解为下列方程组得：

(11)

(12)

(13)

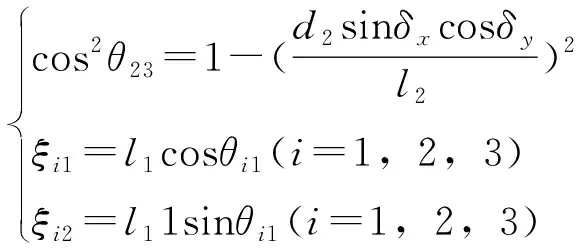
通过以上对电传操纵系统的坐标解算，进一步推导得出了倾斜盘空间指向的表达式，然后建立了操纵机构的运动学模型，为控制分解提供了理论依据。

2 自适应控制器的设计

2.1 自适应律简化

自适应控制在航空航天及空间探测飞行器的控制中大量运用，能消除参数变化与外部干扰对系统性能的影响[14]。工程中许多含有不同量级时间常数的系统都可描述为如式(14)的非线性奇异摄动系统[12-13]

(14)

在式(14)中令ε=0，同时不考虑快变状态z在两个端点处z(t0)=z0和z(tf)=zf的要求，则有

(15)

非线性奇异摄动系统的两点优化问题变换为求最优控制量u[15～16]，只需要求系统的状态x，z从起始状态的x(t0)=x0，z(t0)=z0到终点状态的x(tf)=xf，z(tf)=zf，同时让指标J达到最小。

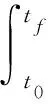
(16)

式中，L为连续的非线性标量函数。

2.2 系统辨识

电传操纵系统的辨识是在系统初始化时进行，需要获取控制的基本参数，然后根据得到的参数写进控制算法，整个辨识过程使用Matlab辨识工具箱，用ARMAX模型辨识出传递函数，建立幅频特性曲线如图3所示，然后基于此幅频裕度进行控制器的参数设计与控制性能分析。

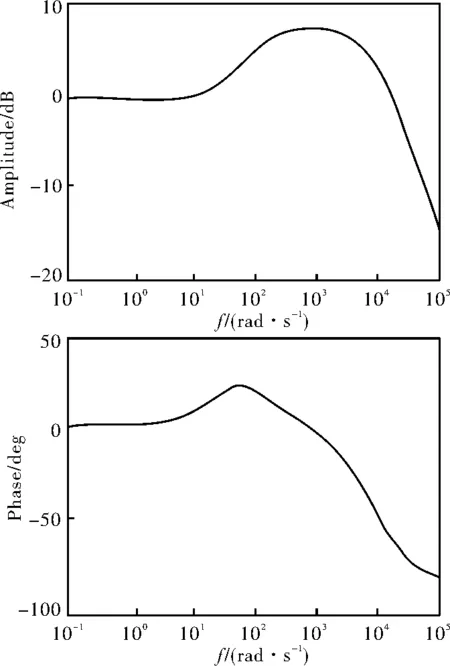
图3 系统辨识的波特图

2.3 结合扫频激励的自适应控制器设计

由于电传操纵系统使用的是永磁同步电机，为了验证前述系统辨识的有效性，获取磁链ψ，定子、转子电阻Rs、Rr，定子、转子自感Ls、Lr等参数，采取正弦扫频信号作为舵机输入激励。扫频函数选取式(16)所表示的函数。

(17)

式中，fl为扫频频率范围的下限，fh为扫频频率范围的上限，t1为扫频过程的持续周期。将得到的电机参数代入下文电机的状态方程式(18)。

永磁同步电机定子两相状态方程为

(18)

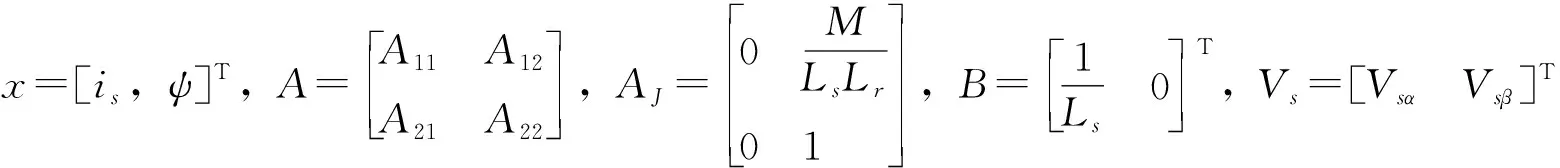
则控制器表示为

(19)

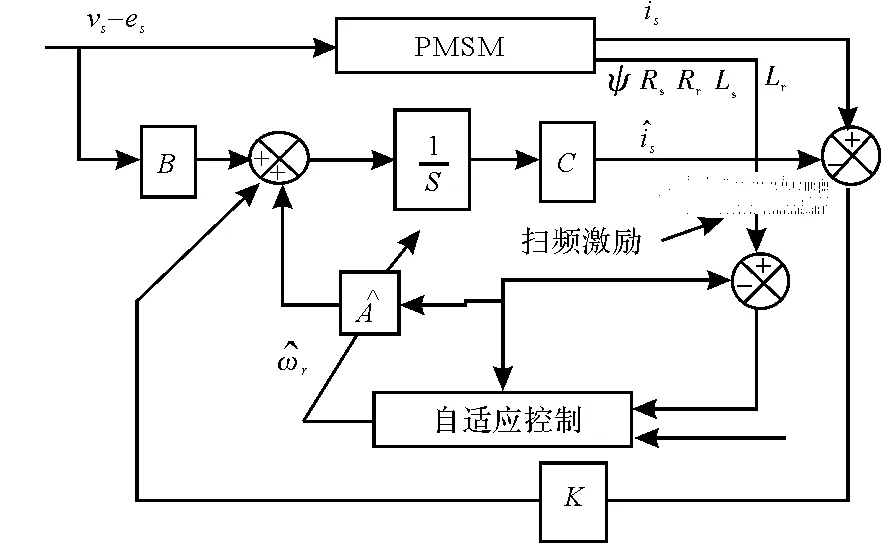
图4 结合扫频激励的自适应控制器结构图

由式(18)、式(19)得到误差方程为

(20)

(21)

电传操纵系统在飞行过程中，随着环境当中的气压、温度等因素的影响，舵机及电路中的电阻、电感等参数会随时改变。由式(21)可知，选择合适的增益矩阵K可以使控制器在一定范围内不会受到电机参数变化而对系统产生影响。

3 实验测试

3.1 实际测试

为了对系统进行多负载测试，分别在30kg、50kg负载下进行电流环的测试，图5为舵机控制与实际电流变化曲线，由图可知，不同负载的实际控制电流略高于期望电流，而且能快速响应期望值，但实际电流和期望电流值保持了很好的跟随性，满足无人直升机电传操纵系统的动力载荷需求。

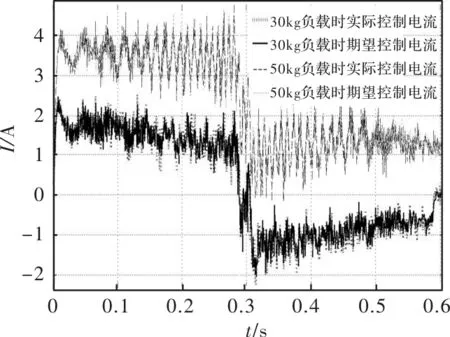
图5 舵机控制电流变化曲线

整个电传操纵系统的外环采取电位计与旋转变压器做综合位置解算，旋转变压器提供内环位置环，电位计作最终位置计算，电位计的电压信号为每个舵机控制提供高精度的位置反馈。如图6所示，飞控给予2.25s的控制指令，驱动电传操纵系统执行动作，整个系统控制误差小于0.05mm，系统控制精度小于1%，满足无人直升机电传操纵系统位置精度要求。

图6 飞控舵面位置指令与实际位置数据图

3.2 性能比较

图7给出了电传操纵系统模拟遭遇外界干扰(如风力)情况下，分别在自适应控制与传统PID控制下的系统响应，从内外到外环路均做出比较。测试给定如下：在系统初始化后，瞬间加载干扰至30kg，然后持续0.4s去掉干扰。从图中可以看出，自适应控制与传统PID控制均能加大电流进行增益调整，达到比较好的位置跟随效果，最终的位置误差都能保持在10-2mm级。但如图所示，无论在电流的利用效率还是响应速度上，自适应控制均明显优于传统PID控制，从图7(b)中可以看出，无论是初始化后的静态还是加载后的动态下，PID控制误差均比自适应控制大，尤其是遇到强干扰时，误差增大2-3倍，由此表明采用自适应控制能让系统具有很强的动静态特性，能快速反应系统环境变化，具有很强的抗干扰能力，起到精确跟随飞行控制指令的目的。

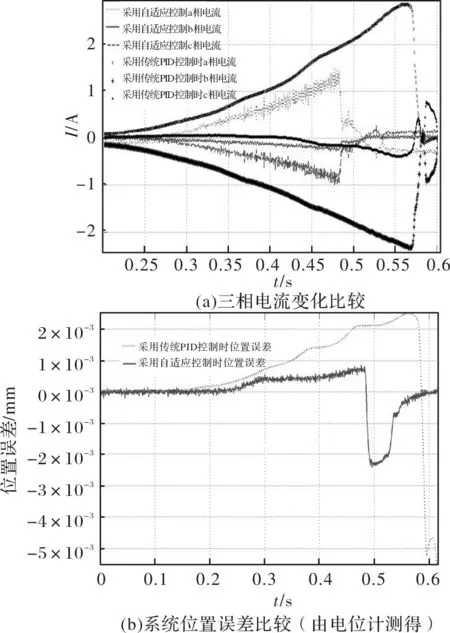
图7 存在环境扰动时不同控制策略性能比较

4 结 语

本文对电传操纵系统进行了坐标解算，运动学的模型分析，进行了正向、逆向运动学推导。根据电传操纵系统在飞行过程中，随着环境当中的气压、温度等因素的影响，舵机及电路中的电阻、电感等参数会随时改变，首先建立系统辨识数据，然后采取扫频技术导入到建立的系统模型中对电传操纵系统进行非线性自适应的控制器设计。最后利用所研发的无人机进行了相关的飞行试验，包括实际的飞行测试以及在强干扰情况下的性能比较，证实所提出的自适应控制方法在此非线性的操纵机构下环境适应能力强，并且可以取得很好的电流、速度、位置跟随与控制效果，整个无人直升机有很好的鲁棒性。