交换环上的w-内射模性质探究
2020-03-26吴明科
吴明科
(西南科技大学 城市学院,四川 绵阳621000)
1 引言
内射模是同调代数中非常重要的模类,本文通过导出函子Ext以及相对w-子模的概念,推广内射模的定义,建立w-内射模。通过讨论将指出w-内射模是内射模的真推广,并利用w-内射模的概念建立w-Noether环的一个等价刻画.在本文讨论中如无特殊说明,提到的环均假设是有单位元的交换环。
2w-内射模
设M是R-模,I是R的w-理想,如果 Ext1(RR/I,M )=0,则称M为w-内射模。由于M为内射模当且仅当对R的任意理想I有 Ext1(RR/I,M )=0,从而得出内射模是w-内射模。
引理1:设M是R-模,A是M的子模。那么A为M的相对w-子模当且仅当GV-tor(M/A)=0。
定理1:设M为R-模,则M为w-内射模当且仅当对任意的循环GV-无挠模模N, Ext(1RN,M )=0。
证明:设M为w-内射模,N为GV-无挠的循环模,显然有N≅R/I,其中I是R的w-理想。
由定义有 Ext(1RR/I,M )=0,所以 Ext1(RN,M )=0;反之,设I是R的w-理想,由引理1有R/I是GV-无挠的,而,则R/I是循环模,所以 Ext1(RR/I,M )=0,所以,M为w-内射模.
定理2:设M为R-模,则以下等价。具体为:①M为w-内射模;②任意同态f∶A→M都可以扩张为同态g∶B→M,其中A是B的相对w-子模,B/A是循环模;③同态f∶I→M都可以扩张为同态g∶R→M,其中I是R的w-理想。
证明①⇒②。根据条件建立如下的正合列0→A→B→B/A→0。其中,A是B的相对w-子模,且B/A是循环模,从而有长正合列
由引理1知,B/A是GV-无挠的,根据定理1可以得到Ext1(RB/A ,M )=0,所以有正合列0→HomR(B,M)→HomR(A,M)→0,显然每个同态f∶A→M都可扩张为同态g∶B→M。
②⇒③,取A=I,B=R,显然是可证的。
③⇒①,建立正合列0→I→R→R/I→0,其中I是R的w-理想,所以得到长正合列0→HomR(R/I,M)→HomR(R,M)→HomR(I,M)→ Ext(1RR/I,M )→Ext1(RR,M)→…,因为 Ext(1RR, M) =0,所以HomR(R,M)→HomR(I,M)→Ext(1RR/I,M )→0,根据条件同态f∶I→M可以扩张为同态g∶R→M,显然有正合列HomR(R,M)→HomR(I,M)→0,所以 Ext(1RR/I,M )=0,则M为w-内射模。
通过上面的讨论,从模扩张的角度建立的等价定义如下所示。
设M为R-模,任意给出的模与同态图形如图1所示。
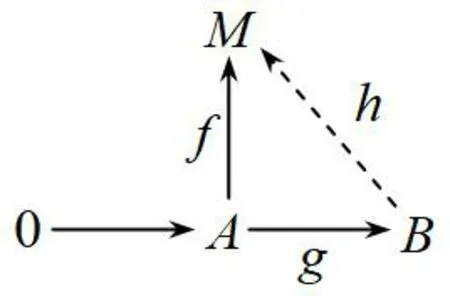
图1 任意模与同态图形
恒存在模同态h∶B→M,使图1完备为一交换图,则称M为w-内射模,其中底行是正合的,并且Im(g)是B的相对w-子模,B/Im(g)是循环模。
从正合列的角度来看,w-内射模有以下结论。
定理4:设M为R-模,则以下等价。具体为:①M为w-内射模;②任意正合列0→M→B→C→0都是分裂的,其中C为GV-无挠的循环模;③对任意的正合列有正合列其中,C是循环的GV-无挠模。
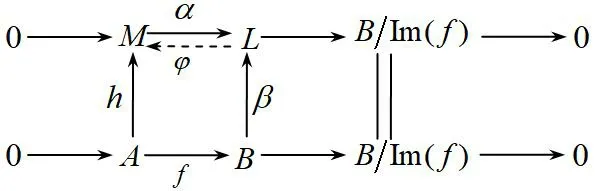
图2 正合交换图
由引理1知GV-tor[B/Im(f)],所以B/Im(f)是GV-无挠模。图2中下行是正合列,因此上行也是正合列,所以由于上行是分裂的,则存在同态φ∶L→M,满足φa=1E。令g=φβ,则有gf=h,因此M为w-内射模。
①⇔③,由定理3显然成立,已经了解内射模是可除模,下面证明w-内射模也是可除模。
定理5:如果M为R上的w-内射模,则M是可除模。
证明,设a是R的一个非零因子,令I=(a),显然可证I是R的w-理想。任取x∈M,并建立同态映射f∶I→M,其中f(ra)=rx。由于M是w-内射模,所以该同态f可扩张到R上,即有同态g∶R→M,使得,则有因此M是可除模。
根据文献[6],设M是R-模,I是R的主理想,如果对任意同态f∶I→M都可以扩张到R上,则称M为P-内射模。
引理2:设R是整环,M是R-模,如果M是w-内射模,则M是P内射模。
特别之处在唯一分解整环,可进一步得到以下内容。
定理6:设R是唯一分解整环,M是R-模,则M是P-内射模当且仅当M是w-内射模。
证明,设M是P-内射模,I是R的w-理想,根据文献[2]得到I是主理想,利用P-内射模的定义,对于任一同态映射f∶I→M都可扩张到R上,因此M是w-内射模;反之,由引理2显然成立。
定理7:设R是唯一分解整环,则每个w-内射模是内射模的充分必要条件是R是Dedekind环。
证明:先证必要性,设M是P-内射模,根据定理6在唯一分解环R上M是w-内射模,由条件M是内射模,根据文献[2]得到R是Dedekind环。再证必要性,设R是Dedekind环,M是w-内射模,根据定理6,M是P-内射模,利用文献[6]得到M是内射模。
在唯一分解整环的条件下,建立定理7的逆否命题如下所示。
定理7':设R是唯一分解整环,则存在一个w-内射模不是内射模的充分必要条件是R不是Dedekind环。
由于作为唯一分解整环,又不是Dedekind环的例子是存在的,例如R=Z[x],因此在R=Z[x]上,必然存在一个w-内射模不是内射模,这样便证明了w-内射模是内射模的真正推广。
3 w-Noether环的一个等价刻画
w-Noether环是经常讨论的一种环类,下面将利用w-内射模在直和方面的性质,建立w-Noether环的一个等价刻画.
引理3:设M是R-模,M=A⊕B,则A是M的相对w-子模当且仅当B是GV-无挠模。
引理5:设有模同态f∶M→N,其中模M是有限型的,且M=(AM)w,A是有限生成的,则
定理8:设R为环,则以下各条等价。具体为:①R为w-Noether环;②任意多个GV-无挠的w-内射模的直和是w-射内射模;③可数无限多个GV-无挠的w-内射模的直和是w-内射模。

通过上面的定理8的讨论,利用w-内射模在直和方面的性质建立w-Noether环的一个等价刻画。
