基于振动频率法准确测量较短吊杆索力的研究

韩亮亮，王行耐，彭霞，王亚飞，张志伟

山东交通学院交通土建工程学院，山东济南 250357

0 引言

目前主要通过施工期间千斤顶准确张拉确定吊杆索力，通过振动频率法反推计算索长作为运营期间吊杆索力评估的参数，可保证较长吊杆的计算精度，但短索吊杆的误差较大，对于成桥安装阻尼装置的吊杆也有较大误差[1-4]。Zui等[5]提出拟合经验公式，利用前两阶振动频率求解索力；Ren等[6]基于能量法将索力影响因子μ引入短索的计算公式，不同的μ对应不同的索力计算公式；Mehrabi等[7]通过有限差分法提出考虑抗弯刚度的短索索力计算公式；李胡生等[8]采用频率分解的方式计算短索索力；陈强等[9]在频率法计算公式中引入索力修正系数α、β及参数η；徐宏等[10]提出“复合边界条件”的计算方法，通过测量吊杆索前四阶振动频率可以较准确地计算短吊杆的实际索力。上述计算方法修正系数较多，部分计算方法需测量多阶次振动频率，较为繁琐，在实际应用中需找到更为准确地拟合公式，快速、准确计算吊杆索力，为工程施工提供可靠数据[11-16]。

本文结合工程实例，分析实际边界条件和抗弯刚度影响，以吊杆振动基频为基础，结合有限元计算分析，修正吊杆实际计算索长并引入修正系数，拟合公式更简单快捷，适用于短吊杆索力计算。

1 振动频率法

振动频率法采用拉索单元线性振动理论测试吊杆索固有的振动频率，通过建立振动频率和索力的计算关系求解吊杆索索力。

计算索力时，考虑动力平衡理论，得吊杆索的运动平衡方程[17]为：

(1)

式中：E为吊杆弹性模量，Pa；I为吊杆截面惯性矩，m4；T为吊杆索力，kN；ρL为吊杆索的线密度，kg/m；x为沿吊杆的轴向坐标，m；t为吊杆索振动时间，s；y为x坐标点在t时刻的横向振幅，m。

对式(1)求解转换，可得一般索力

(2)

式中：K为索力系数；fn为吊杆n阶振动频率，Hz；n为吊杆振动阶次；K=4ρLl2，其中l为吊杆长度，m。不考虑吊杆索的抗弯刚度影响时，式(2)可简化为T=Kfn2/n，计算细长索索力较准确。计算短吊杆索长时，虽可修正实际索长，但由于抗弯刚度的影响，在实际工程中式(2)并不完全适用[17-18]。

2 索力的拟合公式

2.1 拟合公式假定条件

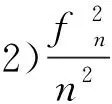
2.2 工程实例

工程主桥桥梁设计为(20+100+20)m三跨简支体系桥，主跨100 m下承式钢箱拱桥，全桥共28根吊杆。进行吊杆张拉时，为保证吊杆张拉力准确及试验结果可靠,采用油压千斤顶和压力传感器同时控制[23-24]；采用索力动测仪测量吊杆振动频率。吊杆上锚点安装阻尼减震构件，下锚点为吊耳式锚头，根据边界条件修正实际吊杆索长，修正安装阻尼减震块的吊索索长从阻尼块算起，未安装阻尼块吊索的计算索长从锚具护筒最前端算起，这种修正方式考虑了桥梁运营期间阻尼装置拆卸不便的情况，修正方式如图1所示，修正结果如表1所示。修正后最短索长为2.171 m，最长索长为14.307 m。

图1 吊杆长度修正方式

表1修正前后吊杆索长m

吊杆编号1#2#3#4#5#6#7#原索长4.5078.05311.01213.38215.16016.34816.943修正索长2.1715.7178.67611.04612.82414.01214.307

2.3 拟合公式计算结果与实测数据

在工程现场进行吊杆张拉试验时，分级控制吊杆张拉力，即张拉过程中张拉力分20%、50%、80%、100%额定张拉力4个加载等级进行张拉，因现场难以准确采集1#吊杆索振动频率，只对2#～7#吊杆张拉过程的吊杆索力进行对比分析，以4#吊杆为例，张拉数据如表2所示。

由表2可知，索长较短时，只考虑抗弯刚度的索力计算公式与实际结果偏差较大，但修正索长后的结果可降低测量误差。

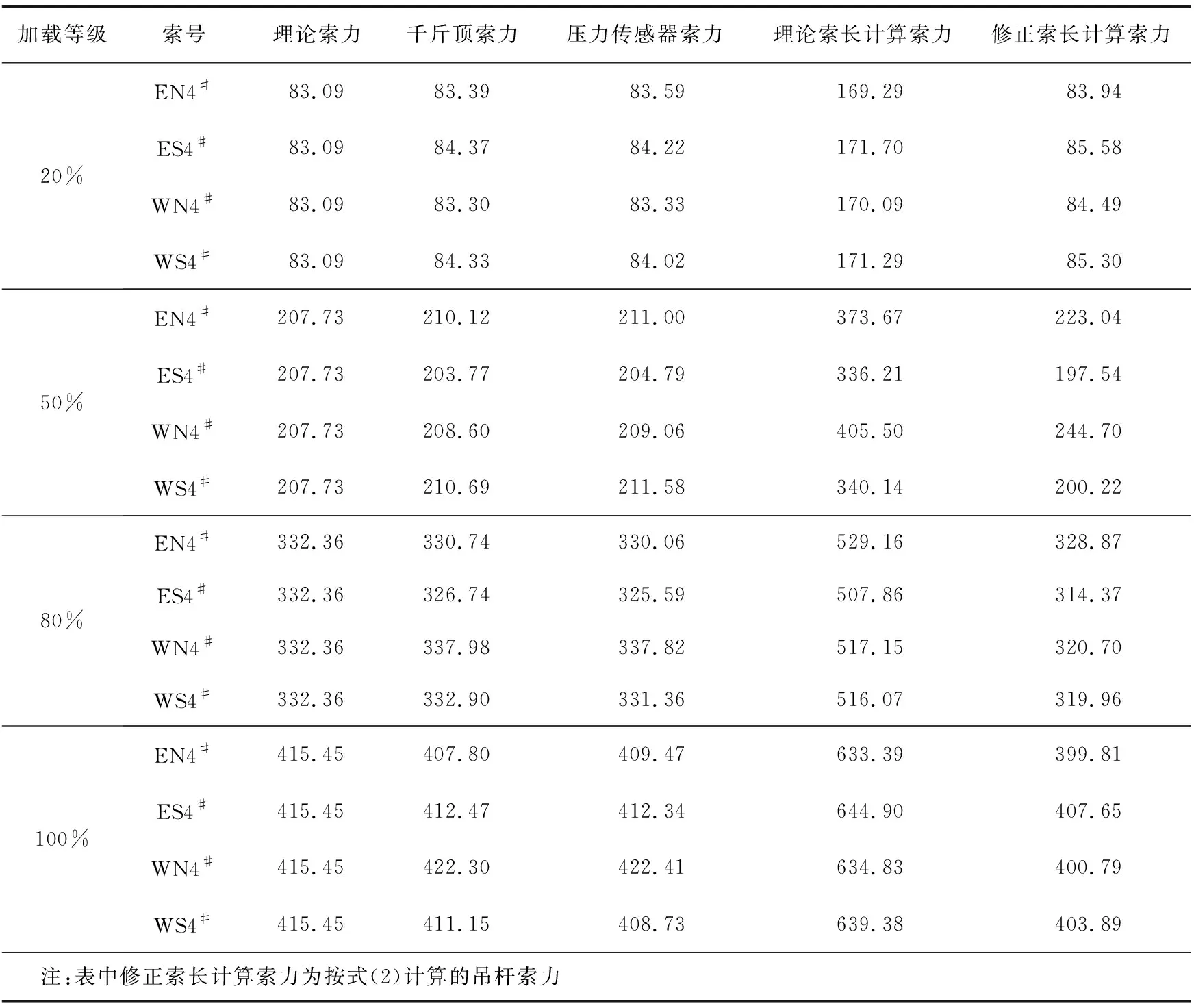
表2 4#吊杆张拉数据对比 kN

2.4 二次修正

经一次修正后索长后仍有一定测量误差，为进一步减小计算结果与实测结果的差距，采用振动频率法测量短吊杆索力时引入修正系数α，则索力

(3)

式中l′为修正索长。

考虑吊杆振动基频，式(3)可简化为：

(4)

2.5 修正索长l′与修正系数α

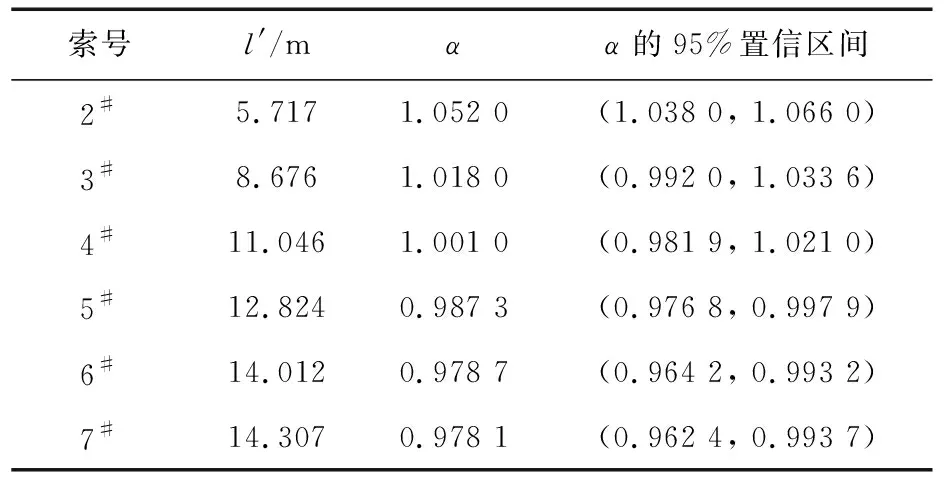
表3 各吊杆修正系数

将表2数据带入式(4)，利用MATLAB对每根吊杆l′的α拟合求解，结果如表3所示。

根据表3，利用MATLAB对l′与α的关系进行拟合[25]，结果为：

α=αl′2+bl′+c，

(5)

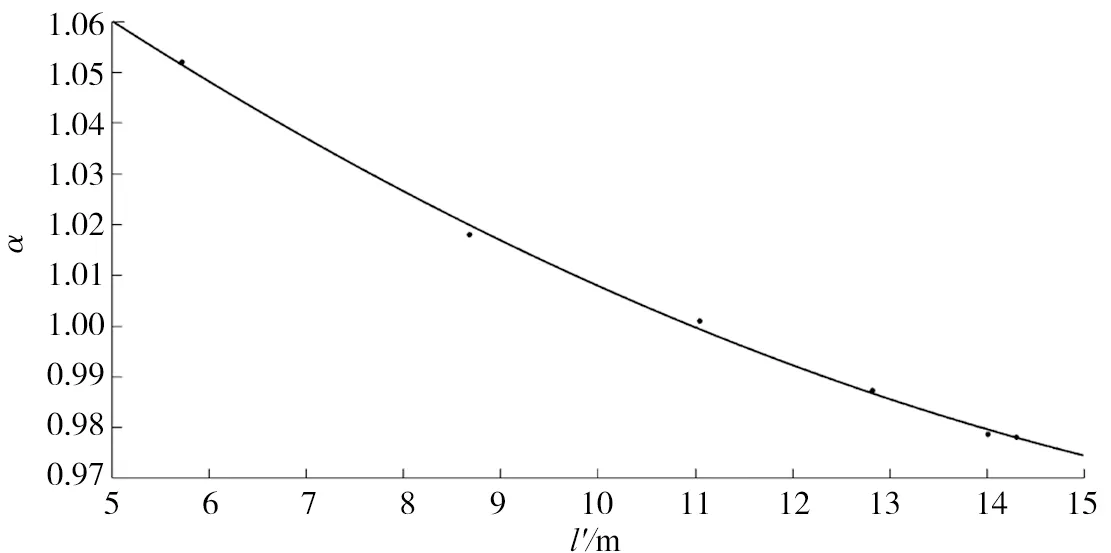
图2 l′与α的拟合关系曲线

由表3得拟合系数a=0.000 374 4，b=-0.016 04，c=1.131。

l′与α的关系如图2所示，则可得各个索长对应的修正系数。

3 拟合公式的适用性

由式(4)计算工程成桥后的索力，结果如表4所示。

由表4可知，式(4)计算的索力误差较小，最大误差为4.92%，符合成桥索力误差小于5.00%的要求。

利用式(4)对其他相似拱桥的吊杆索力进行计算，以验证拟合公式的适用性。某系杆拱桥跨径64 m，全桥拱22根吊杆索，吊杆上锚点安装阻尼减震构件，下锚点为吊耳式锚头，修正后最短吊杆索长4.945 m，最长吊杆索长14.012 m。因在现场难以准确测量1#吊杆索的振动频率，所以仅计算2#～6#吊杆的初次张拉力，结果如表5所示。

表4 成桥索力

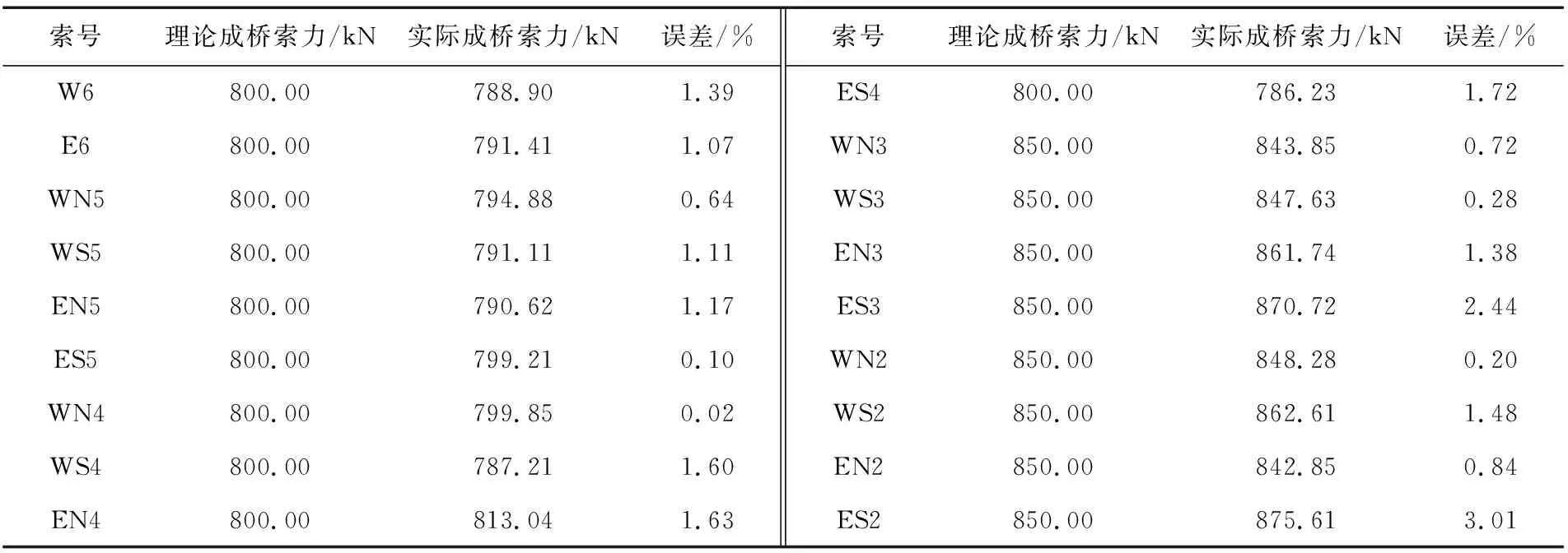
表5 2#～6#吊杆的初次张拉力

由表5可知，索力的拟合公式计算误差均小于5.00%，符合索力控制要求。

为提高拟合公式的可靠性，根据两工程实例索长取值范围，按交集原则，对式(4)索长取值有效区间进行修正并取整，修正后式(4)索长取值的有效区间为[6 m,14 m]。

4 结论

针对一般索力计算公式难以对较短吊杆索索力准确计算的问题，通过实际工程项目提出拟合公式，根据实际情况修正计算索长，引入索长修正系数α的计算公式。在不同工程项目中试验表明，本拟合公式对于修正索长6～14 m吊杆的索力计算结果与实际情况的误差符合施工要求，可作为施工过程中快速测量、计算较短吊杆索力的计算方法。拟合公式考虑了桥梁运营期间实际情况，采集数据时无须拆卸阻尼减震构件，数据采集更加便利可靠。但拟合公式基于准确采集吊杆索基频的前提，这对现场数据采集提出了更高的要求。