基于改进遗传卡尔曼算法的短时路段行程时间估计

林园

上海同济城市规划设计研究院有限公司城市开发规划研究院，上海 200092

0 引言

城市道路交通拥堵问题在我国城市化进程中日益严重,传统的解决方法主要是增加道路和桥梁建设。据统计，车辆数量的增长速度约为道路增长速度的2～3倍[1]。因此，采用成熟的交通信息网络和交通信息提取技术辅助交通管理，已成为缓解当前城市交通拥堵问题的热门课题。

全球定位系统(global positioning system，GPS)在居民日常生活中得到了普遍应用。装载GPS设备的城市浮动车成为交通信息采集的重要节点，浮动车可获得海量的交通数据。有关学者就如何对采集到的数据信息进行筛选和提取、发现数据之间的内在联系、利用数据建立模型、获得动态交通信息等进行了诸多研究，当前已有研究针对特定时间段内的车辆即时运行速度进行计算，从而估计路段行程时间。武小云[2]分别以1、2、5 min 3种间隔为单位时间窗口，对各车辆的平均速度进行统计分析，获取路段的行程时间，选择行程时间序列标准差中离散程度的最小值作为评价标准，但没有考虑车辆在道路交叉口处的延误，降低了对道路行程时间估计的准确度。李宇光[3]采用临近GPS数据点间的运行速度和距离估计各车辆通过道路节点的时间，以数理统计分析方法推测不同道路路段的行程时间。王志建等[4]对低频数据在道路交叉口处相邻定位点的4种分布进行总结，依托车辆运行的速度特征估算通过交叉口的时间，该方法侧重于分析交叉口对车辆运行造成的延误，忽视了非交叉口处车辆运行速度的变化。道路交通状态的变化通常是渐进时变的过程，利用KF算法可以较好地比较和修正车辆运行的时变特征，提高系统状态的预测精度[5-9]。

为进一步优化行程时间预测效果，本文针对数据源本身存在的精度问题，提出用高斯滤波算法优化数据，结合城市GIS信息提出路段地图匹配方法，利用KF算法估计预测道路行程时间。以上海市外环路为例，结合道路线圈测量数据，对路段行程时间估计结果的准确性进行分析。

1 数据格式及预处理

浮动车GPS数据是安装在城市浮动车上的GPS设备采集的车辆定位数据。对于不同的GPS数据采集设备，采集数据格式的标准有所区别。

本文使用的浮动车GPS数据样例如表1所示。

表1 GPS数据格式样例

由于GPS卫星信号在空间传播过程中极易受到环境干扰，造成定位位置数据与实际位置有偏差，同时，浮动车GPS数据包含因漂移等问题产生的噪音数据，严重影响后续道路行程时间的预测精度。因此，采用高斯滤波器对已有数据进行除噪预处理，以减小数据偏差[10]。

对每一个点的坐标(x、y)，滤波后分别为：

图1为高斯滤波前后GPS速度的对比。由图1可以看出：滤波前最大速度约为50 m/s，滤波后的速度均小于10 m/s，滤除了明显不合理的数据，得到与实际情况更符合的数据。同理，对经纬度等数据进行高斯滤波，为下一步的算法提供较好的数据基础。

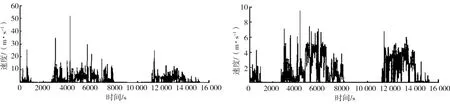
a)滤波前 b)滤波后图1 滤波前后GPS速度对比

2 路段行程时间预测模型

2.1 地图匹配算法

地图匹配算法是一种定位误差修正技术，基本思路是将设备输出的车辆定位点与城市地理信息系统(GIS)中的路网信息相匹配。当GPS浮动车在目标路段的路网范围内行驶时，将GPS定位数据、车辆运行轨迹和电子地图主路数据综合比较，通过合适的地图进行算法匹配。本研究根据位置点到路段的距离以及位置点到候选路段位置角的差值选取匹配路段，将车辆匹配到最近的路段上。地图匹配过程对GPS数据定位的误差要求小于20 m，因此可能会有多个候选路段出现，从候选路段中挑选目标路段的具体规则根据选取的具体算法确定。本文从候选路段中选择与车辆轨迹相似度较高的路段作为目标路段[11]。

GPS速度计算精度在很大程度上与路径搜寻、位置确定有关。地图匹配算法的任务是：选择备选路段，并从中识别出目标路段；将位置点投影到目标路段上，以确定浮动车的实际物理位置。

1)选择候选路段

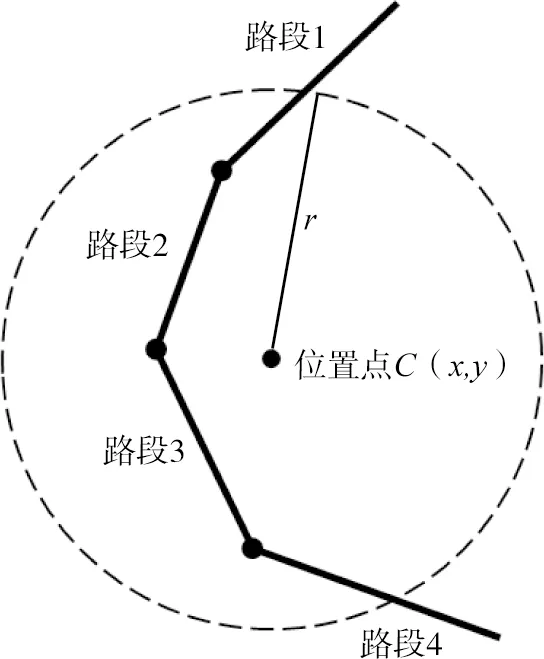
图2 位置点候选路段集

由于GPS设备在定位过程中通常存在定位误差，GPS浮动车的定位坐标总是落于实际位置周边一定范围内，这个范围称为“误差范围”。一般认为，20 m以内的误差不会对结果产生较大的影响[12]。关于误差范围的计算方法已有一些成熟的研究[13]。通常，误差范围假定为圆形或者矩形等形状，为简化计算过程，提高算法运行效率，将误差区域假定为以位置点为圆心，误差距离15 m为半径r的圆形，圆形误差区域内的m个路段构成初始候选路段集Lm，位置点的圆形误差范围与候选路段集如图2所示。

2)候选路段筛选与比对

确定初始候选路段集后，需通过设置条件进一步选择比对路段集。本文主要通过研究位置点到候选路段的最短距离以及两者方向角的差值2个控制变量来确定最终路段集。

假设路段K1(K1∈m)两端点的坐标为P1(x1，y1)，P2(x2，y2)，GPS浮动车位置点的坐标为P3(x3，y3)，如图3所示。点P(x，y)坐标的计算公式为：

计算定位点P3至目标路段K1的距离

式中：a=R(y3)-R(y)，其中R(y3)=πy3/180，R(y)=πy/180；b=R(x3)-R(x)，其中R(x3)=πx3/180，R(x)=πx/180；Re为地球半径。

路段筛选还需用到GPS车辆行进方向角ψ与路段指向方向角θ的差值，即α=ψ-θ，α定义为“误差角”，如图4所示。ψ、θ两者同是以正北方向为0°起始角，顺时针旋转，ψ∈[0°， 360°]，θ∈[0°， 360°]。

图3 点到直线的距离示意图 图4 误差角α示意图

θ的计算公式为：

式中：Δx=x2-x1，Δy=y2-y1。

α的计算公式为：

为保证GPS浮动车行驶方向与路段方向最大可能一致，避免位置点P3匹配到相反方向的路段上，要求α=0～45°。研究表明：当车速低于11 km/h时，GPS浮动车的θ很不稳定，为避免删除可靠数据，此种情况需特殊考虑。1)当瞬时车速大于11 km/h时，α=0～45°，选择P3到路段距离最短的2个路段；2)当瞬时车速小于11 km/h时，选择P3到道路距离最短的4个路段。

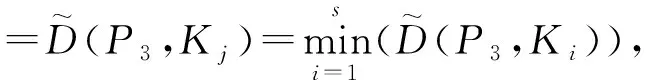
2.2 基于KF的路段行程时间估计

路段行程时间是运行车辆沿某路段从某路口行驶至下个路口所花费的时间，通常根据车辆路段行驶长度与运行速度的比值计算。由于浮动车GPS测量的瞬时速度存在误差，取其测量平均值作为道路行程速度具有较大的不确定性。本文利用KF算法预测路段的行程时间。

短时路段行程时间预测可以根据前几个时段的路段行程时间和时间估计误差确定。为了及时响应路段状况的变化，短时预测以 1 min 为时间间隔，即以路段上第kmin 的路段行程时间预测第(k+1)分钟的路段行程时间[14]。

用k，k-1，…，k-n+1时刻的路段行程时间预测k+1时刻的路段行程时间，模型为：

T(k+1)=H0(k)T(k)+H1(k)T(k-1)+…+Hn-1(k)T(k-n+1)+ω(k)，

(1)

式中：Tk为k时刻的路段行程时间的状态向量，Tk=[ktk]T，其中k为时刻，tk为k时刻的路段行程时间；H0(k)，H1(k)，…，Hn-1(k)为参数矩阵；ω(k)为测量噪声，假设其是均值为零的白噪声，用R(k)表示它的协方差矩阵[15]。

转换式(1)，将其以状态空间形式表达，同时状态空间里的点集以时变参数表示，从而更有利于利用卡尔曼滤波理论对状态变量进行预测估计。则KF的系统状态方程和观测方程为：

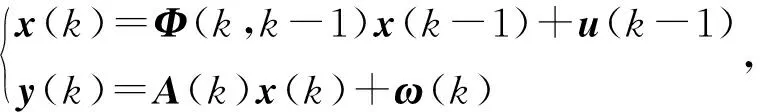
式中：y(k)为观测向量，是滤波的输入；x(k)、x(k-1)分别为k、k-1时刻的状态向量；Φ(k,k-1)为状态转移矩阵；A(k)为转换矩阵，用于将k时刻状态变量映射到测量值所在空间中；u(k-1)为均值为零的高斯白噪声，其协方差矩阵为Q(k-1)。

至此，状态空间表示由原时间序列模型重新构建转换[16]，根据KF算法，其递推方程表达式为：

(2)

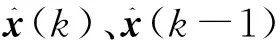
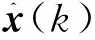
1)算法初始化

令k=k0，确定k0时刻的初始值x(k0)和P(k0)。

2)预测过程

状态预测

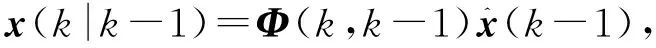
(3)

协方差预测

P(k|k-1)=Φ(k|k-1)P(k-1)ΦT(k|k-1)+Q(k-1)。

(4)

3)计算卡尔曼增益

4)估计过程

状态值更新

协方差更新

P(k)=[I-K(k)A(k)]P(k|k-1)。

(5)

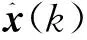
5)循环条件

令k=k+1，重复步骤2)～5)，估计下一个时刻结果。

6)没有新的观测值时，跳出循环。

2.3 基于遗传算法的卡尔曼参数优化

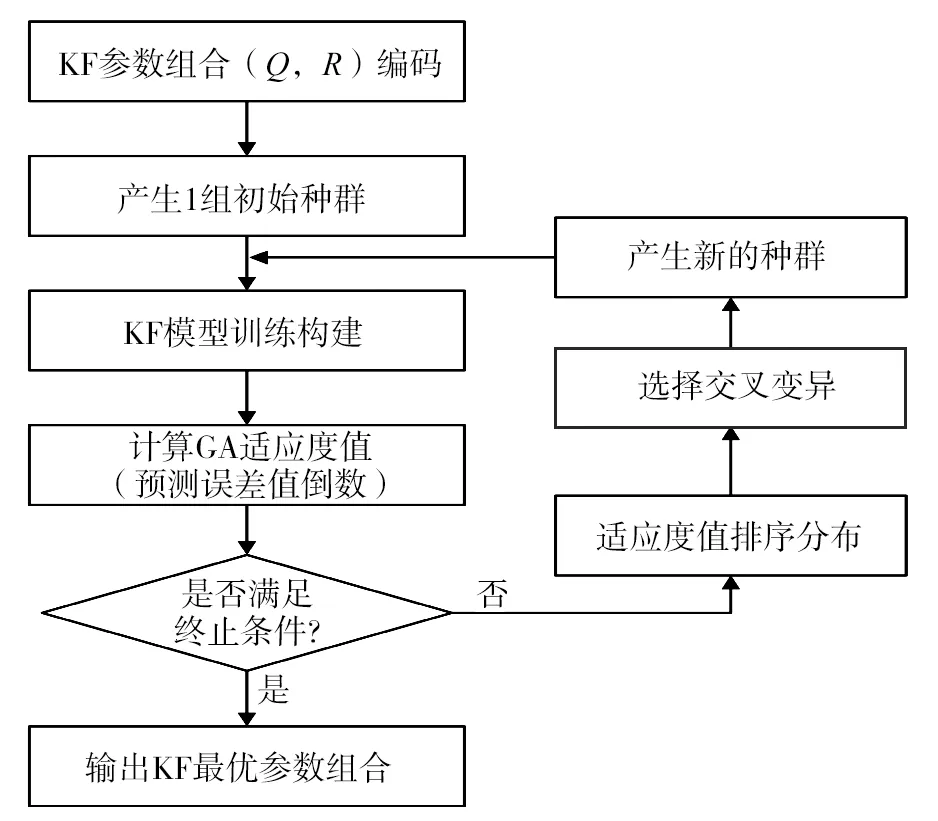
图5 基于GA的KF参数优化

KF算法中的观测噪声协方差和测量噪声协方差是影响KF预测效果的重要参数。由于这2个参数难以直接测量，本文选用GA对这2个参数的初始值Q和R进行联合优化，以达到更加理想的预测效果。该优化流程除使用浮动车GPS数据外，还加入同时段的道路线圈采集的数据，作为车辆运行状态的真实数据。

GA是借鉴自然遗传选择的随机搜索最优化算法，根据自主确定的适应度函数，经历遗传中的选择、交叉和变异对参数个体进行筛选，从而达到更优的参数组合[23-26]，优化流程如图5所示。

优化步骤如下：

1)设置待优化参数Q、R的取值范围为[0，1],且精确到4位小数。对2个参数进行二进制编码，确定染色体编码长度为30，随机生成初始种群。

2)初始化KF算法参数构成的种群。由于GA求解的是极大值，而通过KF算法预测值与道路线圈测量值的误差(绝对值)越小越好，因此取误差的倒数作为GA的适应度，然后确定种群大小、迭代次数、交叉概率和变异率等GA参数，通过“选择-交叉-变异”等遗传选择过程，获取最优参数组合Sopt=(Q,R)，其中Q为优化后的初始观测噪声协方差，R为优化后的初始测量噪声协方差。

3)利用Sopt=(Q,R)训练道路行程时间预测的KF模型，见式(2)。

4)利用训练好的KF模型对浮动车GPS数据进行处理识别，评估模型整体性能。

3 实例分析

本文采用上海外环路2016年8月上传的浮动车GPS数据，共1400万条。浮动车GPS采集频率为1 Hz。本文将道路线圈设备采集的信息作为路段行程时间的真实数据[27]。

利用高斯滤波算法和地图匹配算法对浮动车GPS数据进行处理，采用Matlab软件建立GA-KF模型并进行训练。参数设置：最大遗传代数为60，种群数量为30，交叉概率为0.9，变异概率为0.05，以模型预测值与线圈测量值误差(绝对值)的倒数作为适应度函数。通过GA对参数进行优化，确定初始观测噪声协方差Q=0.563 8，测量噪声协方差R=0.381 6。最后利用GA优化后的KF模型进行各个路段行程时间预测。

图6为对应时刻下路段行程时间预测的部分结果。由图6可以看出：GA参数优化后的KF算法比原始KF算法的预测误差更小，平均提高约7.69 s。

图6 路段行程时间预测结果

图7为对应时刻下路段行程时间实际测量结果与GA-KF预测结果的相对误差。由图7可知：预测误差均在0.5 min内，平均值为0.148 min，预测效果较好。

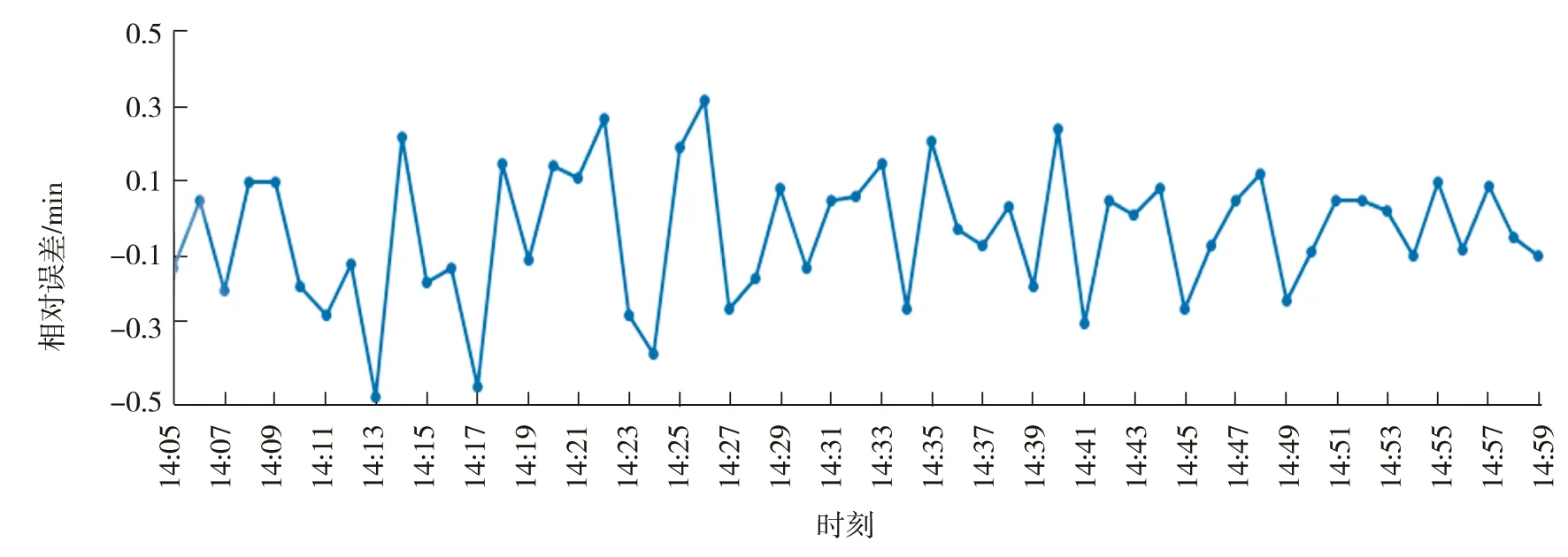
图7 路段行程时间预测相对误差

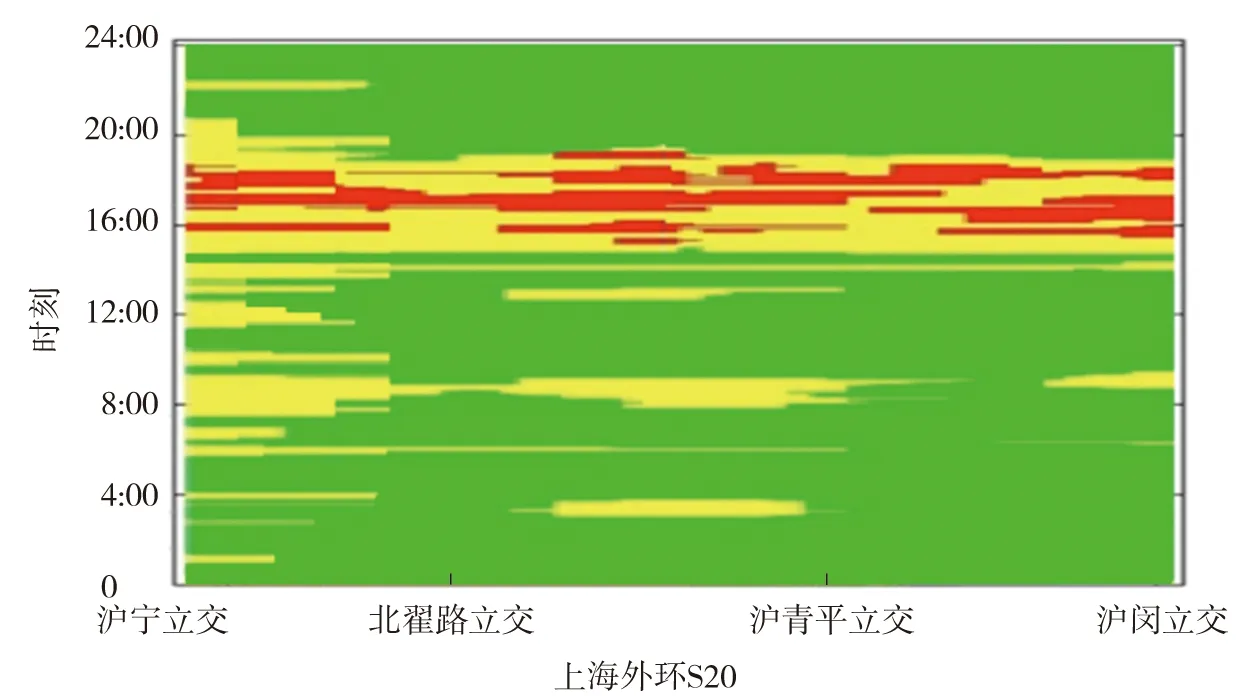
图8 上海外环路段行程车速分布

根据预测得到的路段行程时间，结合GIS中的路段长度，可以得到路段交通流参数中的速度分布，如图8所示，可据此开发城市道路拥堵情况监测平台。图8中:绿色表示当前该路段的车辆行驶速度大于70 km/h，黄色表示路段车辆行驶速度为45～70 km/h，红色表示路段车辆行驶速度小于45 km/h。由图8可以看出：16:00—19:00上海外环路普遍呈现红黄色，表明该时间段内道路处于较为拥堵状态，而早高峰8:00—10:00外环路呈现黄绿色，表明该时间段内道路相对畅通，即早高峰拥堵并不明显。

4 结语

本文利用浮动车GPS数据，建立基于遗传算法优化的卡尔曼滤波模型，与传统卡尔曼滤波器相比，能有效提高预测精度，道路行程时间预测误差小于0.5 min，能够满足实际交通管理的需要。

浮动车数据采集系统得到的数据能较为均匀地覆盖目标道路，较好地补充了当前一些已有固定设备数据采集的缺陷。高速公路上的检测器种类众多，除了GPS浮动车之外还有感应线圈、视频检测、收费站检测、雷达检测等。未来工作将融合多源道路监测数据，以提高道路行程时间预测的效果和时空覆盖率，构建上海市道路状态监测发布平台，为交通管理部门的政策制定提供参考。