人行悬索桥人致振动分析

杨赐，邵志向

中铁第四勘察设计院集团有限公司，湖北武汉 430063

0 引言

本文以某人行悬索桥为工程背景，研究Rayleigh阻尼在选用不同参考频率时对人致振动响应计算结果的影响，提出Rayleigh阻尼合理取值的策略。

1 人致振动和Rayleigh阻尼基本原理

1.1 人致振动

人行走时重心上下波动，同时左右两腿交替支撑，从而产生周期性的竖向动力荷载和水平侧向动力荷载。行人行走的竖向步频为1.7～2.1 Hz(一阶谐波)，侧向步频为0.7～1.0 Hz，这一行走过程被称为“窄带随机过程”[3]20-23。当人行桥上行人密度较大时，必然会有一部分人的步频接近而产生同步效应，当这一同步频率与人行桥的某阶自振频率接近时，将会造成行人与桥结构之间的同步激振，继而造成人行桥大幅度振动[3]57-59。

行人行走荷载模型可采用傅里叶级数展开，为静荷载与几个简谐动荷载之和[2]15-20，竖向荷载

(1)

横向荷载

(2)

其中：m为人的自身质量，g为重力加速度,t为行走时间,fp和fl分别为竖向步频和侧向步频,φvi和φli分别为竖向力和侧向力第i阶谐波相位角,αvi和αli分别为竖向力和侧向力的第i阶动载因子。

模拟n个随机行人组成的行人流，可用n′个完全同步的行人组成等效理想行人流，后者考虑行人之间的同步现象。假设2种行人流对结构的影响相同，但是等效的行人流可作为1种确定性荷载建模[11]，等效同步人群

南宋周密《武林旧事》的记录更有意思了，“小经纪”逐条罗列了杭州城的各种小商品与宠物服务，其中有“猫窝、猫鱼、卖猫儿、改猫犬”，猫窝、猫鱼、卖猫儿的含义好理解，“改猫犬”很可能是给宠物猫、宠物犬做美容。《宋史·孝义传》记载，“江州德安陈昉”之家，“有犬百余，共食一槽，一犬不至，群犬不食”。养了一百多条狗，恐怕就不单纯是出于实用目的，而应该对狗有特别的感情。又据洪迈《夷坚志》，宋人员琦，“养狗黑身而白足，名为‘银蹄’，随呼拜跪，甚可爱。忽失之，揭榜募赎”。这条“甚可爱”的小狗，有名字，有一日丢失了，主人还贴出启事，悬赏寻狗，显然员家已将“银蹄”当成宠物来饲养了。

式中：n为桥面上的随机人数,ξi为结构阻尼比。

由于高阶谐波响应很难同步且影响较小，本文取一阶谐波因子进行计算，采用文献[11]16-18的动载因子，则式(1)(2)可简化为：

(3)

(4)

1.2 Rayleigh阻尼

Raleigh阻尼作为经典的结构阻尼，其表达形式简单，力学概念清晰，可以表示为刚度矩阵和质量矩阵的线性表达式[12]：

C=αM+βK，

(5)

式中：C、M、K分别为结构的阻尼矩阵、质量矩阵和刚度矩阵，α为质量矩阵系数，β为刚度矩阵系数。

根据正交性原理，任意一阶模态阻尼比ξi和自振频率ωi满足

(6)

联合结构两阶固有频率ωi和ωj，并代入式(6)，可求得

(7)

通常假定各阶模态的阻尼比相同，即ξi=ξj=ξ，则有：

(8)

2 实例分析

2.1 工程概况

某大跨度人行悬索桥是单索面地锚式悬索桥，主桥跨径为400 m，主梁为双分离式箱型加劲梁，采用拱形桥塔。桥梁单幅宽度为8.5 m，从跨中到桥塔左右两幅单箱梁的距离由2 ～16 m曲线变化，顺桥向俯瞰主梁似X形。人行悬索桥效果图、整体立面图及主梁跨中断面如图1～3所示(图2、3单位为cm)。

图1 某人行悬索桥效果图

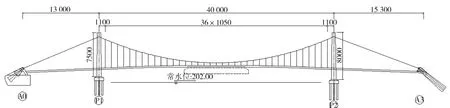
图2 某人行悬索桥整体立面图

图3 某人行悬索桥主梁跨中断面图

2.2 建模

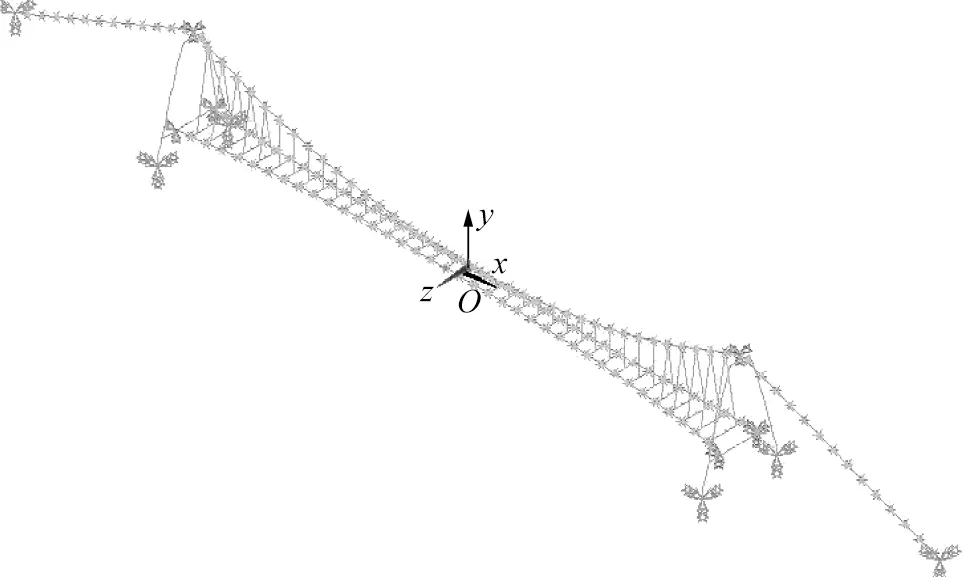
图4 某人行悬索桥全桥有限元模型

根据式(1)～(8)编制ANSYS程序，计算人行悬索桥全桥三维有限元模型人致振动时程响应[13-14]。该人行悬索桥主梁为钢箱型加劲梁桥，根据文献[15]，取阻尼比为0.005。文献[16-19]表明，行人在桥面上正常行走时人群密度通常为0.2～1.5 人/m2，本文取人群密度为1.0 人/m2。由于人的自身质量m、步行速度v的差异性影响较小，取重量G=mg=800 N，v=1.5 m/s。

利用ANSYS软件建立符合实桥结构的有限元模型，主塔、加劲梁、刚臂结构采用空间梁单元BEAM4模拟，主缆与吊杆采用空间杆单元LINK10模拟，桥面铺装、护栏、索夹、锚头等质量及质量惯性矩采用节点质量单元MASS21模拟，如图4所示。桥塔基础模拟为固结结构；主梁梁端支座处设置竖向约束、横向约束和扭转自由度，其他自由度释放；主缆两端在桥塔处与主塔鞍座位置处进行自由度耦合。

人行悬索桥有限元模型前65阶模态竖向自振频率及振型如表1所示。

表1有限元模型前65阶竖向振动频率及振型Hz

阶次频率/Hz振型描述30.229一阶反对称竖弯40.307一阶正对称竖弯50.418二阶正对称竖弯70.623二阶反对称竖弯150.921三阶正对称竖弯211.277反对称竖弯311.703正对称竖弯阶次频率/Hz振型描述372.740正对称竖弯492.941两根主梁交错竖弯513.348反对称竖弯553.521两根主梁交错竖弯604.020正对称竖弯654.165两根主梁交错竖弯

从表1中可得：仅第31阶模态频率(1.703 Hz)处于竖向步频敏感频率范围内，当行人同步频率与此频率相等时，实桥结构将有可能产生较大的激振。故取式(3)中fp=1.703 Hz。本文仅分析竖向人致振动响应，侧向人致振动的分析方法与竖向类似，故不再过多阐述。

2.3 计算结果

当实桥结构处于弹性阶段时，振型叠加法计算的动力结果可作为实桥结构的真实响应。以此计算结果为基准，采用不同的两阶参考频率，构造不同的Rayleigh阻尼矩阵，研究阻尼矩阵对人行悬索桥人致振动响应计算结果的影响：工况1选取振型叠加法计算结构振动响应为比较基准；工况2选取第3阶频率(一阶反对称竖弯)和第4阶频率(一阶正对称竖弯)；工况3选取2个第31阶频率进行计算(人致振动敏感频率范围)；工况4选取第3阶频率(一阶反对称竖弯)和第31阶频率(人致振动敏感频率范围)；工况5选取第3阶频率(一阶反对称竖弯)和第65阶频率(较为靠后的竖弯模态)。

不同工况的计算结果进行相对误差分析，采用公式

式中：e为相对误差，Δ1为工况1的人致振动时程响应，Δi表示工况2～5的人致振动时程响应。

利用式(3)(4)，将工况1～5的人群荷载加载到ANSYS三维有限元模型进行动力时程分析。工况2～5采用Rayleigh阻尼，按照式(8)采用不同的两阶参考频率计算，工况1采用模态叠加法和固定模态阻尼比。不同工况下人行悬索桥人致振动位移时程s和加速度时程a响应结果如图5～9所示，不同工况下结构振动响应的相对误差如表2所示。

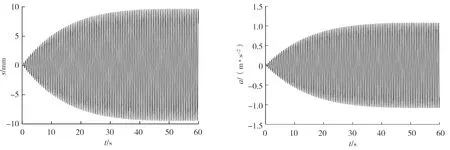
a)位移 b)加速度图5 工况1人行悬索桥人致振动位移时程和加速度时程响应

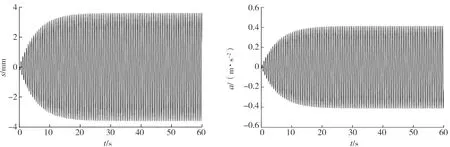
a)位移 b)加速度图6 工况2人行悬索桥人致振动位移时程和加速度时程响应

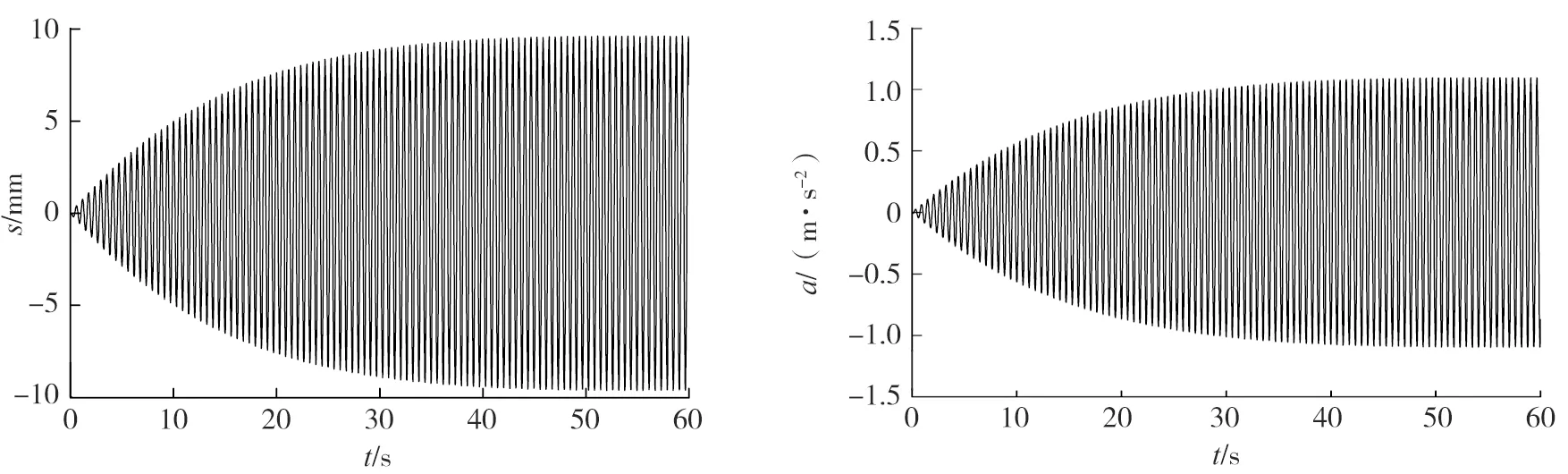
a)位移 b)加速度图7 工况3人行悬索桥人致振动位移时程和加速度时程响应

a)位移 b)加速度图8 工况4人行悬索桥人致振动位移时程和加速度时程响应

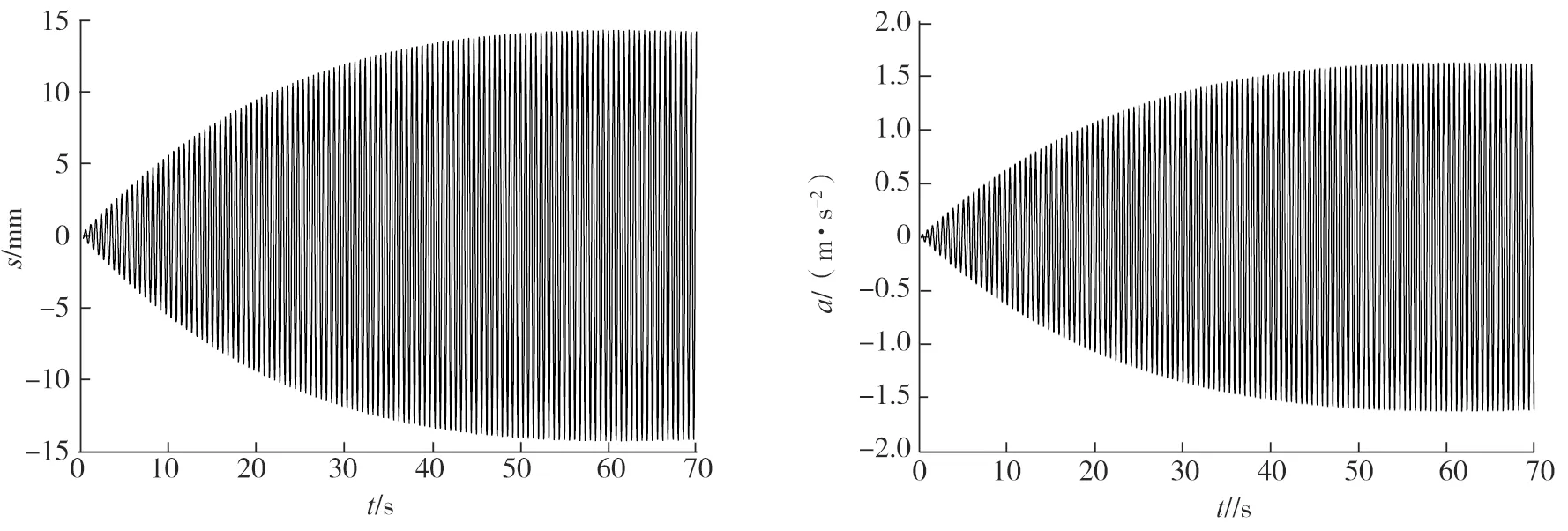
a)位移 b)加速度图9 工况5人行悬索桥人致振动位移时程和加速度时程响应

表2不同工况下结构振动响应误差

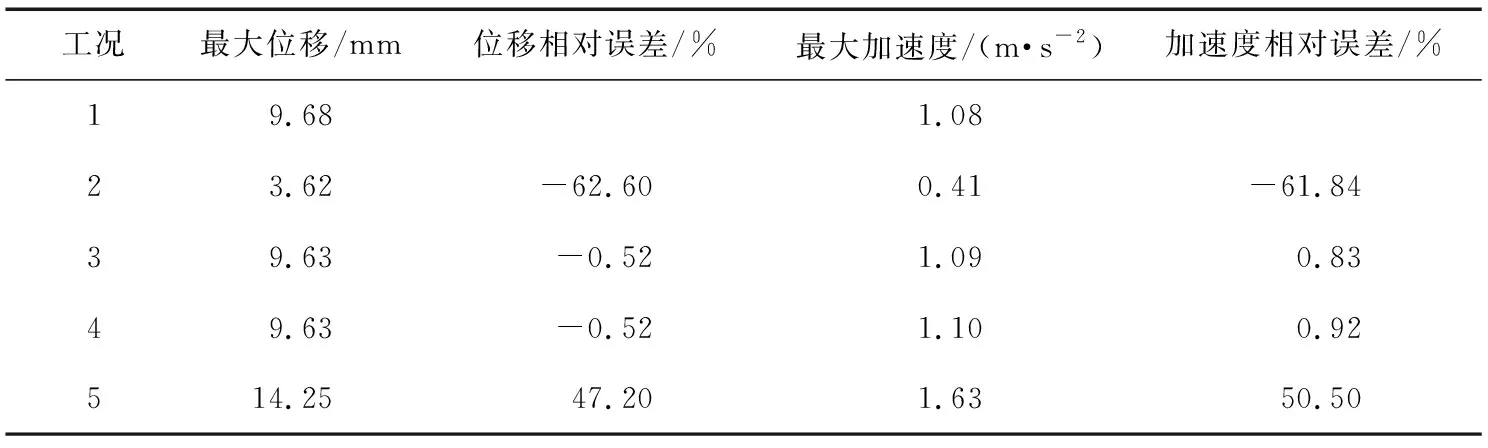
工况最大位移/mm位移相对误差/%最大加速度/(m·s-2)加速度相对误差/%19.681.0823.62-62.600.41-61.8439.63-0.521.090.8349.63-0.521.100.92514.2547.201.6350.50

从图5～9和表2中可以看出：1)工况2采用第3阶和第4阶频率，即一阶反对称竖弯和一阶正对称竖弯，这两阶模态是实桥结构最先出现的2种竖弯振型，其竖弯频率远小于人致振动敏感频率，其位移和加速度响应均低于工况1，结构的振动响应被低估。2)工况3采用两个第31阶竖弯频率，该两阶模态频率均处于人致振动敏感频率范围内，工况3的结构振动响应计算结果与工况1比较接近。3)工况4采用第3阶和第31阶竖弯频率，即一阶反对称竖弯和一阶处于行人敏感频率范围内的竖弯模态，可以看出工况4结构振动响应与工况1大致接近。4)工况5采用第3阶和第65阶竖弯模态，即一阶反对称竖弯和一阶较为靠后的竖弯模态，可以看出工况5动力响应明显高于工况1，动力响应明显被高估。通过以上计算分析表明：Rayleigh阻尼选取不同的两阶参考频率对人致振动响应结果影响显著，因此，选取合理阻尼参考频率对计算结果的可靠度非常重要。

2.4 误差原因分析

通过两阶参考频率计算获得不同工况下的Rayleigh质量矩阵系数和刚度矩阵系数，代入式(6)，反推出Rayleigh阻尼矩阵其余各阶竖弯模态的阻尼比。各工况下模态阻尼比ξ与竖弯频率f的关系曲线如图10所示。

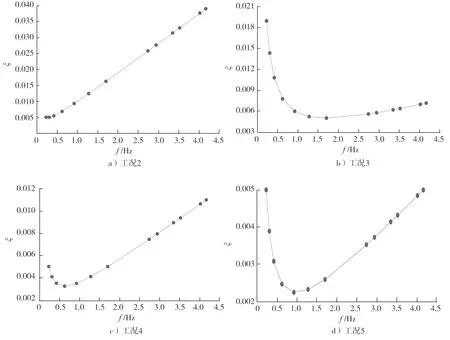
图10 各工况模态阻尼比与竖弯频率的关系曲线

从图10中可以看出：1)工况2中，第3阶和第4阶竖弯模态的ξ=0.005，其余各阶模态ξ均大于0.005，且随着频率的增大而不断增加。处于竖弯敏感频率范围(1.7～2.1 Hz)内的模态振型ξ=0.016～0.020，远高于指定ξ=0.005。ξ增大，实桥结构振动响应被缩小，计算结果偏不安全。2)在工况3中，仅第31阶模态ξ=0.005，竖弯敏感频率范围(1.7～2.1 Hz)内的结构模态ξ=0.005～0.0051，非常接近指定模态ξ=0.005，对人致振动响应的计算结果较为真实。3)在工况4中，第3阶和第31阶模态ξ=0.005，两者之间的模态ξ<0.005，最低为0.0032。竖弯敏感频率范围(1.7～2.1 Hz)内的结构模态ξ=0.005～0.0059，很接近指定模态ξ=0.005，结构计算反应较为真实。4)在工况5中，第3阶和第65阶模态的ξ=0.005，两者之间的模态ξ远小于0.005，最低可达到0.0022。竖弯敏感频率范围(1.7～2.1 Hz)内的结构模态ξ=0.0026～0.0029，远低于指定的模态ξ=0.005。由于ξ减小，实桥结构的振动响应被夸大，计算结果过于保守。

由此可看出：将处于敏感频率范围内的结构模态ξ模拟的较为准确时，其响应计算结果真实可靠。而敏感频率范围外的模态ξ不管是增大还是减小，其对动力响应的计算结果影响比较小。行人敏感频率范围内的结构模态振动对人行悬索桥的人致振动结构响应起主导地位，类似于地震中的“卓越周期”，所以在进行人致振动时程分析时，要综合考虑输入荷载和结构动力特性的影响，保证敏感频率范围内的结构模态ξ模拟准确，使计算结果更加真实可靠。

3 结论

以某大跨度人行悬索桥为工程背景，编制ANSYS分析程序进行人致振动时程计算，研究Rayleigh阻尼在选取不同两阶参考频率进行计算时对结构振动响应结果的影响。

1)进行人行悬索桥人致振动计算时，结构敏感频率范围内的模态振动对结构动力响应的贡献占主导地位。

2)敏感频率范围外的模态ξ的变化对动力响应的计算结果影响不大。

3)在实际运用中，综合考虑输入荷载和结构动力特性的影响，针对控制设计的部分选取合理的参考频率来确定Rayleigh阻尼矩阵，以准确反映人行悬索桥敏感频率范围内的振动模态ξ。