基于ICA-RBF神经网络的沥青混合料疲劳性能预测

李友云，王中恩*，张彪,2

1.长沙理工大学交通运输工程学院，湖南长沙 410114；2.湖南路桥建设集团，湖南长沙 410004

0 引言

沥青混合料疲劳性能的预测研究越来越受到道路工作人员的重视，现行路面结构设计规范将沥青层疲劳开裂作为沥青路面设计的控制指标。各国科研人员对疲劳性能提出了不同的研究方法，建立针对沥青混合料自身影响因素的疲劳预测模型，但不同区域的研究成果存在一定的差异[1-8]。20世纪60年代，Monismith等[9]建立基于应变控制的疲劳寿命预测模型。吴宏宇等[10]认为沥青混合料的疲劳性能受众多因素影响，常规方法难以准确、有效预测，提出采用混沌神经网络模型预测沥青混合料的疲劳性能。谭忆秋等[11]采用BP神经网络预测沥青混合料的体积参数，并结合灰关联法分析得到体积参数的主要影响因素，通过调整网络内部的结构形式，最终建立预测模型。袁斌等[12]认为荷载条件、环境条件及沥青混合料本身性质对疲劳性能产生一定影响，已往的疲劳试验方程并不能完全体现出各变量之间的复杂关系，提出采用遗传算法结合神经网络研究不同变量对疲劳性能的影响，最终建立了疲劳性能预测模型。只考虑单一变量的数据分析与试验对研究疲劳性能难度较大，研究人员提出了多变量预测模型[13-15]。

对比分析不同预测方法后，本文采用帝国竞争算法结合神经网络预测模型，并量化不同因素间的权重，对多变量下沥青混合料疲劳性能的研究具有一定意义。

1 网络模型

径向基(radial basis function，RBF)网络是一种3层前馈神经网络，结构较简单，收敛速度较快，逼近能力较强，在解决函数拟合和分类问题中应用广泛。其隐藏层神经元以径向基函数为激活函数，输入数据离隐层神经元数据中心的距离越远，输出结果越小。假设样本总数为P，m个输入层，n个隐藏层，l个输出层，则m-n-l结构RBF网络可表示为：

(1)

式中：f(x)为输出层神经元的激活函数，ρj为第j个隐藏层的径向基函数，cj为数据中心值，Wjk为第j个隐藏层与第k个输出层间的连接权值。

假设网络隐藏层神经元有P个样本数据，数据中心即为各样本数据，径向基函数的宽度设为定值，此时网络参数只有输出权重未知，依次将样本输入网络，组成一个方程组，再使用最小二乘法，求得输出权重。在采用RBF神经网络训练时，通常要确定隐层节点数(数据中心个数)、数据中心、扩展常数及输出权值4类参数。RBF神经网络的训练过程就是确定参数的过程。完成一次网络参数更新后，重复RBF网络正向计算与参数梯度更新过程，直到网络的误差函数e<ε，ε为预定误差。

帝国竞争优化算法(imperialist competitive algorithm，ICA)是通过模拟殖民地同化机制和帝国竞争机制而形成的一种算法。ICA也是一种基于群体的优化方法，其解空间由称为国家的个体组成。ICA将初始群体分为几个子群，称为帝国，在每个帝国内，ICA通过同化机制使非最优国家(殖民地)向最优国家(帝国主义国家)靠近，最优国家(帝国主义国家)之间也会相互竞争合并，最终竞争合并成一个帝国。帝国竞争算法有很好的全局收敛性和普适性，与下降算法不同，其对求解域无可微或连续要求，求解稳定；算法本身对样本依赖性不大，即使样本有部分缺陷，也不会影响全局最优结果；利用竞争算法得到能量最大的帝国，将此帝国中的殖民国变量作为最优网络权值和阈值，把这些变量应用到神经网络的初始权值和阈值中，克服常规神经网络易陷入局部最优的不足，保证预测模型性能，提高预测精度[16-18]。

结合RBF网络与ICA的优势，采用梯度法更新RBF网络参数，利用ICA对RBF网络的参数进行全局寻优，最终获得基于ICA的RBF网络，构建ICA-RBF优化神经网络模型。

2 疲劳试验

2.1 混合料的设计

以AC-13C型沥青混合料为试验载体，采用石油SBS改性沥青，集料采用玄武岩矿料，填料采用石灰石矿粉。原材料各项技术指标都满足文献[19]中关于沥青、集料、矿粉的要求。

按照AC-13C级配设计要求及已往工程试验，一般采用油石质量比为4.5%～6.5%，同时满足文献[19]的要求，故选择4.5%、5.0%、5.5%、6.0%四种不同油石质量比制作马歇尔试件，以达到神经网络检验样本数据的理想覆盖率。

2.2 疲劳试验方案

采用UTM伺服液压沥青混合料动态试验系统HYD-25进行劈裂强度及疲劳试验，采用应力控制模式进行疲劳试验，在15 ℃时进行间接拉伸疲劳试验，选取0.2、0.3、0.4、0.5四种不同的应力比，荷载波形采用连续正弦波，疲劳试验加载频率分别为5、10、15 Hz。

2.3 试验结果

参照文献[20]的劈裂疲劳试验资料，设置不同变量及沥青混合料疲劳试验条件，在52组多变量因素试验结果中随机选取12组作为模型检验样本，结果如表1所示。

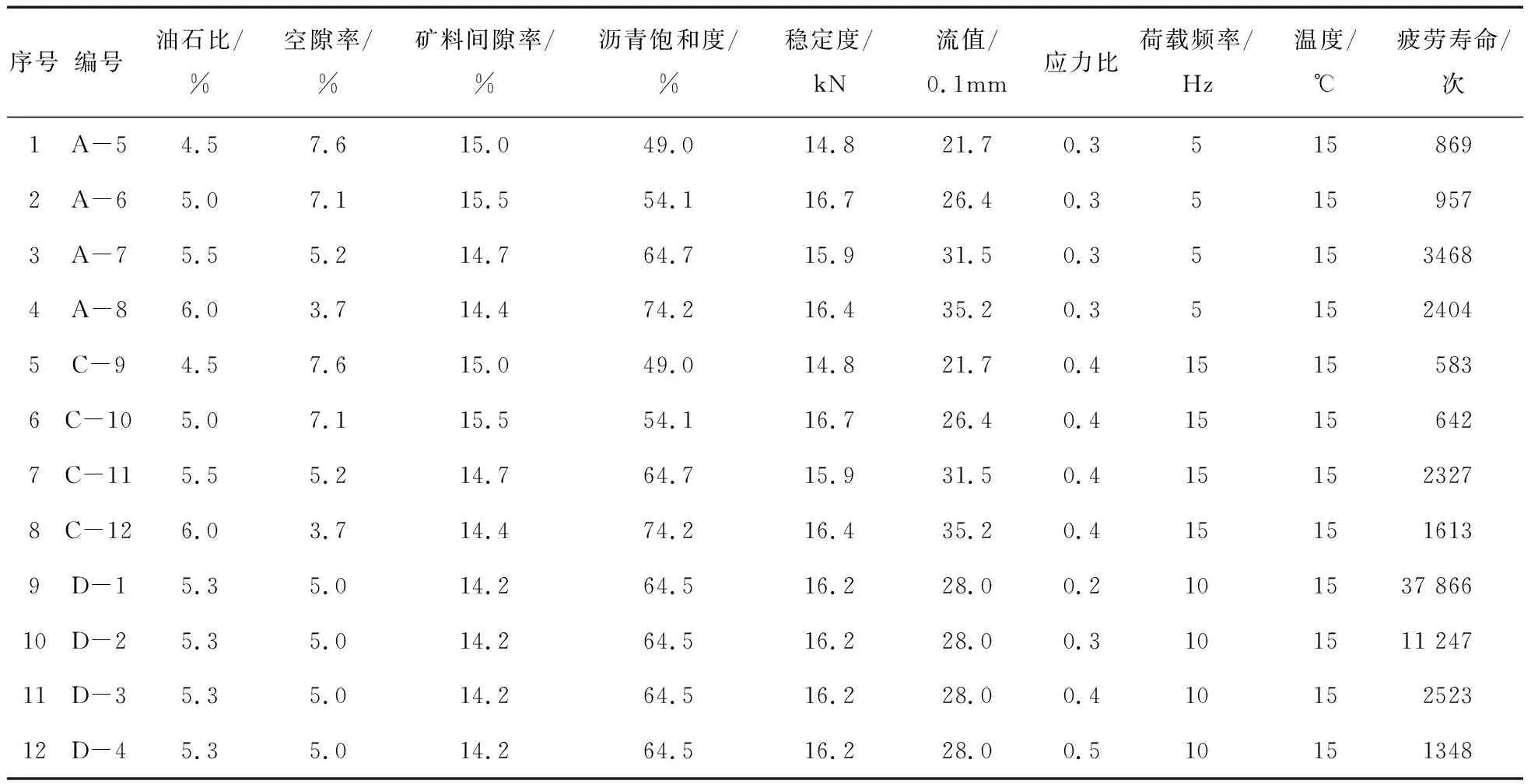
表1 不同条件下12组检验样本的疲劳试验结果

3 模型预测和对比

参考文献[21]的编辑程序，在MATLAB上建立多变量沥青混合料疲劳性能预测模型，并分析比较其预测效果，从而得到最优疲劳性能预测模型。为对比各算法的优越性，预测过程中对不同算法的模型设定数据处理模块，只需将试验数据按程序要求整理为训练集和检测集，由MATLAB自动运行，将输入数据集划分为训练集、验证集与检验集，并通过运算得到相应预测结果、误差分析及预测公式的输出参数，根据这些输出参数对预测模型进行评估与选择。根据统计学对数据集的划分依据(训练集、验证集、检验集在所选取数集所占比例分别为50%、25%、25%)，结合实际情况，从52组疲劳试验数据随机选用12组作为检验样本，剩余部分归入训练样本，输入参数即为疲劳性能的影响变量(即油石比、空隙率、矿料间隙率、沥青饱和度、稳定度、流值、应力比、荷载频率)。

3.1 疲劳寿命的预测模型

RBF算法的预测模型分为导入数据、归一化处理、RBF神经网络、结果输出4个模块，无需调节隐藏层层数。在检查训练集检测情况时，出现了过拟合情况，使得预测结果失真，由此判断BRF神经网络模型对疲劳性能的预测结果不稳定，在选择疲劳预测模型时应避开。

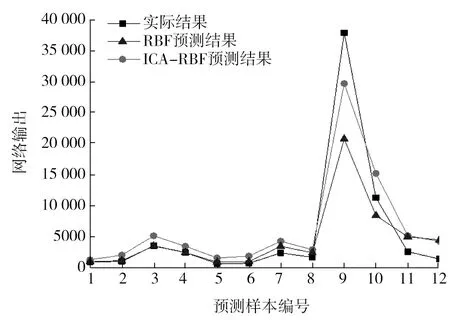
图1 两种网络模型的预测结果曲线

在RBF网络模型基础上建立的ICA-RBF神经网络优化预测模型，无需调节隐藏层层数，运算时间较长。ICA-RBF优化算法预测模型结构较复杂，大致分为使用ICA训练径向基网络、数据的输入、归一化处理、RBF参数、网络参数的形状、根据PrimitiveStates产生殖民地集合、调试时考虑缩小VarMin和VarMax、算法参数的设定、learnRBF、结果输出等10个模块。

RBF和ICA-RBF两种模型的预测结果曲线如图1所示，两种预测模型网络输出误差如表2所示。

由表2可知，ICA-RBF预测模型的结果优于RBF预测模型，但在预测过程中，RBF预测模型训练集中的验证集出现了过拟合效应，表现不稳定；优化模型优于一般神经网络模型，虽然ICA-RBF预测结果的平均相对误差比RBF高，但ICA-RBF模型更稳定，整体精度也较高。

表2 两种预测模型网络输出误差对比

3.2 权重

神经网络预测模型的优势为可量化对比不同因素间的权重。在学习过程中，网络的输入层和隐藏层之间的连接权矩阵可根据实际数据不断调整优化，探究数据间的映射关系，在一定程度上权重反映该指标对结果的影响程度。因此，可依据输入层到隐含层间的连接权矩阵V计算各变量的权重，各变量的权重[22]

(2)

式中：ωj为第j个输入项的权重，m为输入项个数，k为隐藏层节点数，vij为第j个输入项在第l个节点对应的权值。

由式(2)导出ICA-RBF预测模型的权值矩阵V、权向量W，并代入变量权重ω的计算公式，得到各影响因素的权重。根据ICA-RBF预测模型的权值矩阵V可知，隐藏层共20层，有9个输入节点，其中HN1～HN8分别与油石比、空隙率、矿料间隙率、沥青饱和度、稳定度、流值、应力比、荷载频率这8个变量对应，-1输入层对应HN9，然后由式(2)计算各影响因素所占权重，结果如表3所示。

表3 各影响因素的权重

由表3可看出：外荷载及混合料空隙结构对疲劳寿命影响较大，符合工程实际情况。实际疲劳试验结果表明：相同条件下，荷载作用越大，材料结构性能越差，其疲劳试件所测得的疲劳寿命越短。

4 结论

基于常规RBF神经网络算法的理论学习，结合RBF网络与帝国竞争算法的优势，采用梯度法更新径向基网络参数，利用帝国竞争算法对径向基网络参数进行全局寻优，最终获得基于帝国竞争算法的RBF神经网络算法，构建ICA-RBF优化神经网络模型。

1)优化神经网络可处理多变量因素预测问题，通过调整内部节点的权值与阈值逼近复杂的非线性关系，适用于沥青混合料疲劳性能的预测。

2)优化神经网络模型同样具备量化对比不同因素间权重的优势。根据预测结构中各变量权重比值可以看出，沥青混合料疲劳寿命在一定程度上受外荷载影响较大。数据显示应力比对寿命的影响大于孔隙率、流值等因素。

3)对比RBF神经网络模型和ICA-RBF优化神经网络模型可知，均方根误差、拟合优度两项指标显示ICA-RBF模型优于RBF模型。虽然ICA-RBF模型预测的平均相对误差比RBF模型大，但在训练过程中，RBF模型训练集中的验证集出现过拟合效应，表现不稳定。因此，ICA-RBF模型更加稳定且整体精度更高。