基于EViews的国内客车销售发展趋势分析

王艳杰，韩广德，闫安，王国泰

山东交通学院汽车工程学院，山东济南 250357

0 引言

我国的客车生产从以中外合资及技术引进为主到自主研发生产为主，种类从最初单一的柴油客车拓展到新能源、纯电动、氢能源客车等，目前已达到世界领先水平，产品远销全世界60多个国家。由于近几年飞机、高铁、地铁等交通方式的快速发展，人们对交通出行方式的选择更加多样化，长途客车的需求量有所降低，节假日高速公路通行费减免以及共享汽车、电动汽车的大力推行，在一定程度上抑制了公路客运的发展。客车行业经历了2008—2015年的快速发展期后，从2016年开始客车销量逐渐下滑，公路客运量下降。

1 我国客车行业的发展现状

1.1 客车销售现状

我国作为世界最大的客车市场，主要以生产销售宇通、中通、比亚迪、金龙等品牌客车为主，其产品在国内市场的占有率高达90%，国际市场占比达30%以上[1]。近几年客车销量如图1所示。

由图1可知：客车销量在2008—2015年快速增长，在2015年销量达到顶峰,为57.15万辆;从2016年开始连年下滑，2018年降至最低,为48.5万辆。

车型不同，销售情况不同。大型客车降幅较大，2018年全年销量仅7.7万辆，较2017年下降18%，而中小型客车以及校车整体减幅相对较小[2-3]。

1.2 公路客运量

近10 a的公路客运量如图2所示。由图2可知：2009—2012年公路客运量稳步增长，自2013年开始，客运量逐年下降。这是因为：自2013年起，铁路与民航客运量、私家车拥有量出现较大增长，以滴滴出行、神州租车为代表的出行平台开始快速推广，使公路客运受到影响。

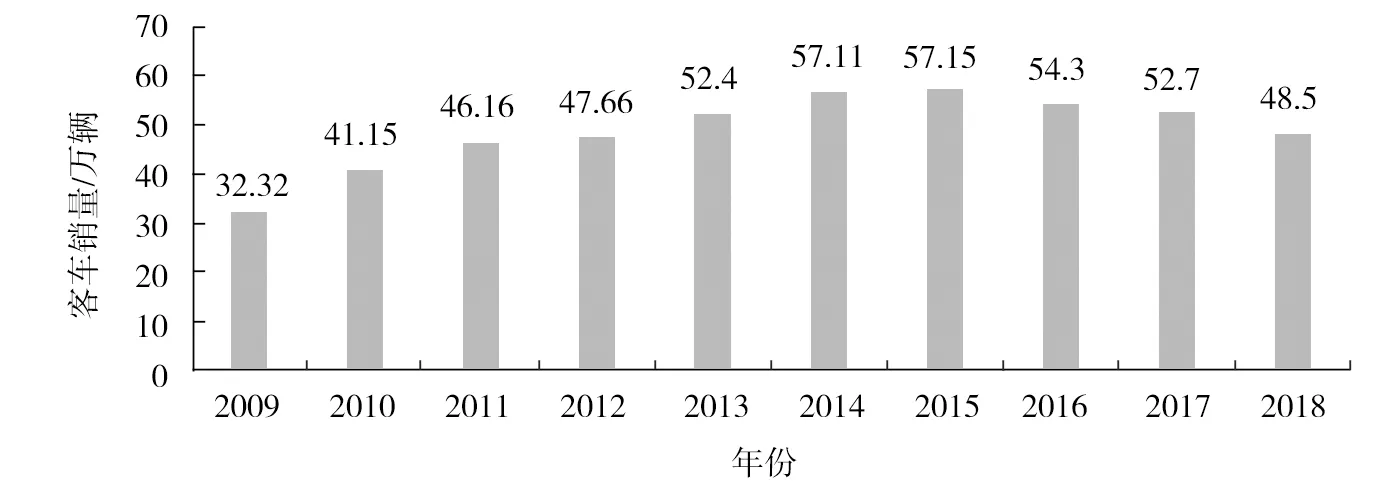
图1 2009—2018年客车销量

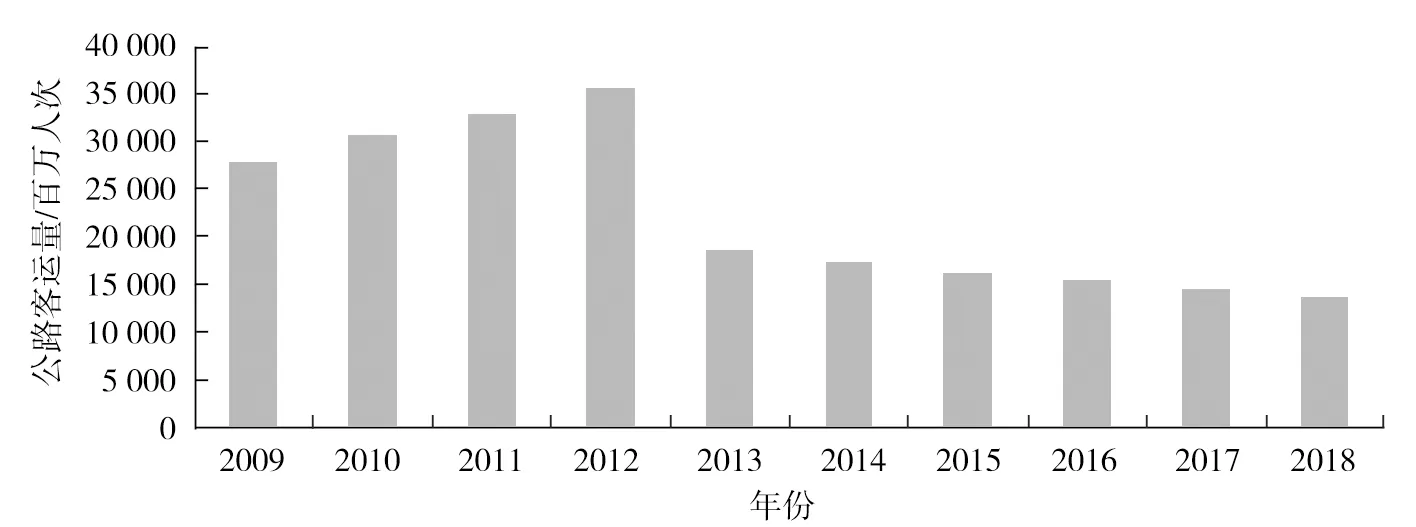
图2 2009—2018年公路客运量

2 影响客车销量的因素

1)国内生产总值

国内生产总值(GDP)是一个国家经济实力最重要的宏观衡量标准。2018年中国的GDP为90万亿元，占全世界GDP总量的1/6。国家GDP的增长给国家工业带来了发展机遇，客车行业也不例外[4-5]。

2)国家政策

国家将新能源客车的研发列入“863计划”，从2010年起国家开始对新能源客车实施补贴，对客车企业在新能源技术研发以及市场推广方面投入了大量资金，促使新能源客车市场迅速发展，截至2018年底，新能源客车的销量已达到91 642辆。但随着新能源汽车补助标准的降低，客车销量开始出现下滑[6-8]。2019年新能源客车补贴额度下降幅度较大，国家政策向纯电动客车与氢能源客车倾斜[9]，加上国五排放标准汽车的禁售，这些对柴油客车市场都造成较大的冲击。

3)轨道交通客运量

轻轨、地铁等轨道交通的快速发展，减缓了城市公交车的发展速度。城市公交车在整个客车销售市场份额占比高达70%以上，故轨道交通客运量是影响整体客车市场的重要因素[10-11]。近10 a轨道交通的客运量如图3所示。

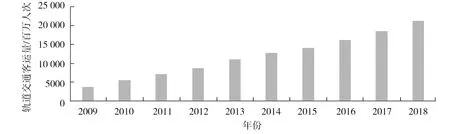
图3 2009—2018年轨道交通客运量

4)公路里程

日益增长的公路里程使交通网络四通八达，为长途客运、中短途客运、城际客运、公路货运提供了保障，所以公路里程是影响客车销量的主要因素。

5)铁路营运里程

21世纪以来，中国的铁路里程居世界第一，高铁平均运行速度居世界第一。铁路建设的快速发展，影响了人们的出行选择，长途客运量明显减少，故铁路营运里程是影响客车销量的主要因素。

6)其他因素

轻量化设计、智能化控制等客车制造关键技术的应用，发动机、高性能车桥等客车主要零部件产业基础的发展,客车企业的知名度与国际影响力以及车型的实用性与经济性等因素对客车市场也有较大影响[12-13]。

3 线性回归模型的构建

3.1 变量的选取与数据收集

客车销量作为因变量y，选取国内生产总值x1、轨道交通客运量x2、公路里程x3、铁路营运里程x4等影响客车销量的因素作为自变量，并以表1所示2009—2017年的统计数据(数据来自中国国家统计局-数据查询)作为参考，建立多元线性回归模型，利用EViews软件进行参数估计，并对模型的相关性进行检验[14]，确定拟合优度系数较高、概率低于0.01的影响因素，建立多元线性回归模型[15]。

表1 2009—2017客车销量及影响因素

3.2 模型建立与检验

3.2.1 多元线性回归数学模型的建立

根据表1中的数据建立多元回归模型：

y=β0+β1x1+β2x2+β3x3+β4x4+μ,

(1)

式中：β0～β4为偏回归系数,μ为随机干扰项[16]。

基于EViews软件,运用普通最小二乘法得出模型(1)的拟合优度系数R2=0.891 097，表明模型的拟合程度一般，且显著性检验未通过，回归效果不好,因此，对模型(1)进行合理调整，经过多次建模与检验分析，建立新的客车销量与各影响因素间的多元线性回归模型

lny=β0+β1lnx1+β2x2+β3x3+β4lnx4+μ。

(2)

基于表1、式(2)，借助EViews软件，利用最小二乘法进行参数估计[17]，线性回归结果如表2所示。表2中的T检验是对自变量的显著性检验，F检验是对模型(2)的显著性检验。

表2 线性回归结果

由表2可知：拟合优度系数R2=0.995 696，F检验值对应的概率较小，表明该模型的拟合程度较高，lnx1、lnx3、lnx4的T检验概率均较小，但x2的T检验概率比较大，表明变量x2可能不适用于该模型，或者存在多重共线性[18]。

3.2.2 多重共线性检验

表3 各因素间的相关系数

通过EViews软件得到各因素之间的相关系数，分析自变量和因变量间的相关程度，如表3所示。

由表3可知：x2、x3均与lny正相关，但在表2中这两个自变量的回归系数为负值，即与lny为负相关，结果相互矛盾；x3与lnx4、x3与x2之间的相关系数大于0.99，呈高度相关，存在多重共线性[19]。所以需要对模型进行进一步检验，并确定是否删除其中的某些因素。

3.2.3 逐步回归分析

运用逐步回归法解决模型(2)中的多重共线性问题[20]。

将表1中各自变量分别代入模型(2)，在给定的显著性水平下，分别建立一元回归方程,对每个自变量进行T检验，并对比各自变量的拟合程度，从中选取对y影响显著的变量所对应的方程作为一元回归初始模型。在一元回归模型的基础上逐步引入其他变量，建立二元回归方程。以此类推将变量逐一引入方程，最终建立多元回归方程。每一步都需要对各变量进行T检验，如果因为引入某一变量而使模型变得不再显著时，则将该引入变量删除。直到将所有的显著变量都引入回归方程，剔除不显著的变量，则逐步回归验证结束。同时也要对已选定的影响因素依次进行F 检验[21]。

1)一元回归模型检验

对lny与lnx1、x2、x3、lnx4进行回归分析检验，一元回归模型分析结果如表4所示。

表4 一元回归模型分析结果

由表4可知：lnx1对应的R2最大，表明模型对因变量拟合的较好，因变量的真实值更接近拟合值。且T检验的概率最小并小于0.01，因此lny受lnx1的影响最大，故综合考虑，选择y=f(lnx1)作为二元回归模型检验的初始回归模型。

2)二元回归模型检验

对y=f(lnx1)与x2、x3、lnx4进行回归检验，其回归分析结果如表5所示。

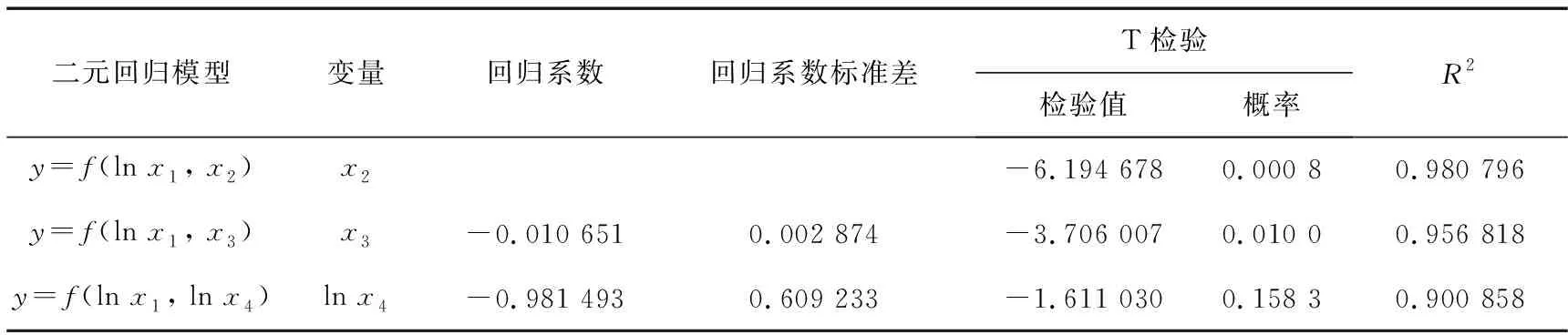
表5 二元回归模型分析结果

由表5可知：x2对应的R2最大，且T检验的概率最小并小于0.01，lny受x2的影响最大，因此将y=f(lnx1，x2)作为三元回归模型检验的初始回归模型。

3)三元回归模型检验

对y=f(lnx1，x2)与x3、lnx4进行回归检验，其回归分析结果如表6所示。

表6 三元回归模型分析结果

由表6可知，x3、lnx4T检验的概率远大于0.01，且对应的T检验值的绝对值小于T检验的临界值4.032，所以三元回归中的T检验未通过验证。

经过上述逐步回归检验，去除公路里程x3、铁路营业里程x42个因素，保留轨道交通客运量、国内生产总值作为自变量，建立新的线性回归模型

lny=β0+β1lnx1+β2x2+μ。

(3)

3.2.4 相关性检验

对新建模型(3)重新进行检验，利用T检验、DW检验(判断模型的自相关状态)和F检验方法判断用最小二乘法估计出来的参数的优劣程度。

基于表1、式(3)，在EViews软件中，利用最小二乘法进行参数估计，得到线性回归结果，如表7所示。

表7 新建模型的线性回归结果

由表7可知，R2=0.980 796，表明模型拟合效果很好，进一步对该模型进行相关性检验。

1)F检验。由于选取了9个样本(2009—2017年数据)，且自变量数量为2，在0.01的显著水平下，由表7可知，F的统计值为153.215 4，远大于临界值10.925，伴随概率为0.000 007，远小于0.01，所以模型通过F检验[22]。

2)T检验。表7中自变量项系数对应的概率分别为0.0001、0.0008，且对应的T检验值的绝对值大于T检验的临界值3.707，自变量均通过了显著性检验[23]。

3) DW检验。在0.01的显著水平下，依据样本容量和自变量数由文献[21]得：DW的下临界值DL=0.408 000，上临界值DU=1.389 000，由表7可知，该模型的DW=2.499 897，因为DU

综上所述，模型(3)通过了相关性检验，基于表7中的数据，最终建立客车销量的多元线性回归模型

lny=-8.358 190+0.986 610lnx1-0.023 241x2。

(4)

3.2.5 实例验证

采用回归模型(4)，对我国近10 a的客车销量进行实际销量与预测销量的对比检验，结果如表8所示。

表8 客车实际销量与模型预测销量对比 万辆

2018年我国轨道交通客运量高达2 127 659万人次，国民生产总值GDP为90.030 95万亿元，经模型预测2018年销量为50.60万辆， 2018年我国客车的实际产、销量分别为52.05、48.5万辆，预测结果与实际销量相差较小。将2009—2017年的国民生产总值和轨道交通客运量的数据分别代入模型对客车销量进行预测，与实际销量相比，绝对误差较小，准确度较高。说明多元线性回归模型(4)的预测具有较高的准确性。

4 结论

1)客车销量与轨道交通客运量正相关，随着轨道交通客运量的增加，客车销量呈现上升趋势。说明轨道交通的发展在某种程度上激增了客车的需求量，因此要加快客运供给侧改革，运用“互联网+”，尽快实现客运与传统铁路、城际轨道交通和城市轨道交通的无缝衔接，促进客车行业的发展。

2)客车销量与国内生产总值负相关。GDP的提高促进了家用汽车市场的发展，也促进了人们消费形式及出行方式的多元化发展，私家车、网约车、共享汽车、高铁及飞机等便捷出行方式的发展对客车市场有一定的抑制作用。建议：我国客车企业注重技术创新，在节能与减排技术方面加大研发力度、提高客车智能化水平；扩大海外市场，避免产能过剩；完善服务体系，提升用户满意度。