鹅掌楸人工林生长最优模型选择研究
2020-03-25朱祥锦
朱祥锦
(福建省政和县林业科技推广中心,福建 政和 353600)
鹅掌楸(Liriodendron chinense)又名马褂木、双飘树,为木兰科(Magnoliaceae)鹅掌楸属落叶大乔木,是我国特有的古老孑遗树种,现列为国家二级珍稀濒危保护植物[1—4]。鹅掌楸干形挺拔通直、材质优异且纹理均匀细致,常用于制作高档家具和工业用材,在立地条件较好的山地种植表现出显著的速生丰产性[5]。此外,鹅掌楸的落叶可将雨水吸持渗入,起到涵养水源、保持水土的作用,落叶分解成腐殖质,将N、P、K等养分元素归还林间,又可改良林地土壤[6—8]。鉴于鹅掌楸经济价值和生态价值突出且用途多样,福建省将其列为用材林基地建设中优先发展的树种并广泛种植[9]。近年来,关于鹅掌楸的研究颇多,但主要集中在杂交育种、种苗繁育、木材性能、适生性、园林绿化应用、逆境胁迫等方面,而对鹅掌楸合理轮伐期的确定具有重要意义的人工林生长过程的研究及模型拟合则尚无人涉及[10—16]。为此,笔者在鹅掌楸人工林中选择标准株进行树干解析,并对其树高、胸径及材积生长与造林时间建立数学模型,以期筛选出拟合程度高、最能反映鹅掌楸人工林生长的方程式,为鹅掌楸以及其他树种人工林生长期的判定和划分提供理论依据,促进人工林经营水平的提升。
1 样地概况
鹅掌楸人工林样地位于石门林场场部工区66林班95 大班6 小班,面积9.8 hm2,地理坐标118°38′22″~118°38′36″E,27°19′40″~27°19′59″N,海 拔 346 ~457 m 。 该 林 分 前 茬 为 杉 木(Cunninghamia lanceolata)人工林。2009 年采用挖大穴回表土的方式营造鹅掌楸人工林,造林密度每公顷2400 株。样地所在区域地处武夷山脉东南,鹫峰山脉西北坡。受中亚热带季风湿润气候影响,年均温18.4 ℃,日极端最高气温40.1 ℃,日极端最低温度-7.6 ℃;年均降雨量1590.5 mm,年均蒸发量1498.4 mm,年均相对湿度78%;年均日照时间1952.5 h,年均无霜期262 d。土壤类型为黄红壤,土层厚度 1.5 m 以上。林下植被以五节芒(Miscanthus floridulus)、观音座莲(Angiopterissp.)为主。
2 试验方法
2.1 标准地的设置与标准木选择
在试验样地内按品字形设置3 个30 m×30 m 标准地。通过每木检尺测定标准地内鹅掌楸的胸径、树高。然后每块标准地选择1 株平均木作为标准木。2018 年10 月,将标准木在根颈部伐倒,在0 m、1.3 m、2 m 处及2 m 之后按1 m 的区分段分别锯取一个5 cm 厚的圆盘。在圆盘非工作面标注解析木号数、区分段号、南北向等信息进行解析。
2.2 生长模型建立与筛选
将解析木圆盘的工作面刨光、打磨使其剖面光滑、年轮清晰,采用LA2400 Scanner 扫描仪以600分辨率扫描圆盘图像,通过年轮宽度换算各龄级生长量,采用中央断面区分求积法计算各区分段材积以及标准木整株材积。然后用Excel 软件绘制胸径、树高、材积生长量与生长年限的散点图,并通过添加趋势线初步判断其所适应的数学模型。在DPS V15.10 数据处理系统中采用Logistic、Webull、二次曲线等13 个有代表性的数学模型逐一进行方程拟合[17]。根据拟合结果,选择决定系数(R2)最高的为最优生长模型,若决定系数相同,则以残差平方和最小的模型为最优[18]。
2.3 模型验证
根据优选出的数学模型,计算鹅掌楸各龄阶胸径、树高及材积的理论值。采用F统计检验法、偏差统计量法以及预测精度检验法对鹅掌楸的胸径、树高和材积生长模型进行检验和评价[19]。
3 结果与分析
3.1 鹅掌楸胸径生长模型选择
将鹅掌楸胸径生长的实测数据依次采用Logistic、Webull、二次曲线等数学模型进行拟合,各数学模型的拟合方程及决定系数、残差平方和如表1。除Michaelis Menten、Quadratics Ratio 两个模型拟合效果稍差,另11 个数学模型均能较好地拟合鹅掌楸胸径(D)与林龄(T)的回归关系。其中Webull、二次曲线、Gompertz、Johnson Schumacher、Morgan Mercer Florin、Peal-Reed 和Richards 等7 个模型的拟合效果最佳,决定系数均为0.9994,高于其余6个模型。但Webull、二次曲线、Gompertz、Johnson Schumacher、Morgan Mercer Florin、Peal-Reed 和Richards 模型的残差平方和分别为0.3443、0.3922、0.3621、0.3464、0.3531、0.3470、0.3630。说明Webull模型D=75.6887{1-e-[(T+2.3354)/19.5656]^3.1489}较其他12种模型能更好的拟合鹅掌楸胸径与林龄的回归关系,是鹅掌楸胸径生长模型的最佳选择。
3.2 鹅掌楸树高生长模型选择
采用Logistic 等13 个数学模型对鹅掌楸树高生长进行拟合,13 个模型均能较好地拟合树高(H)与林龄(T)的回归关系(表2)。除Michaelis Menten、Quadratics Ratio、Yield Density 模型的决定系数低于0.9900,其余10个模型的决定系数均高于0.9972,其中Webull、Morgan Mercer Florin 模型拟合的决定系数均为0.9999,高于其他11 个模型。但Webull模型的数学方程的残差平方和为0.0405,Morgan Mercer Florin 模型拟合的数学方程的残差平方和较0.0405 要小,说明Morgan Mercer Florin 模型的拟合效果更优于Webull 模型,是13 个数学模型中鹅掌楸树高生长的最优模型,该模型的数学方程为H=(55.5498+34.2298T1.9310)/(119.6386+T1.9310),其决定系数为0.9999,残差平方和为0.0367。
3.3 鹅掌楸材积生长模型选择
鹅掌楸材积拟合的系列数学方程、决定系数、残差平方和见表3。其中决定系数因拟合数学方程的不同而呈现较大分化,决定系数最大的数学模型有3 个,分别是Webull、Gompertz 和Richards 模型,其决定系数均为0.9999,Logistic、二次曲线、Johnson Schumacher、Peal-Reed、Yield Density 的决定系数分别为0.9993、0.9809、0.9716、0.9982、0.9894,相对Webull 等3 个模型较小,但均在0.9500 以上。而Gauss、Michaelis Menten、Morgan Mercer Florin、Cubics Ratio、Quadratics Ratio 等5 个模型的拟合效果相对较差,决定系数分别只有0.7474、0.5151、0.7615、0.8630、0.6509。拟合效果最好的3 个模型中,以 Webull 模型的残差平方和最小,为0.00001544。综上,鹅掌楸较好的材积生长模型为Webull 的V=2.5736{1- e-[(T-2.2455)/16.3381]^3.8741},T为林龄。

表1 鹅掌楸胸径生长拟合数学模型Table 1 The Fitting results of DBH growth mathematical model of Liriodendron chinense

表2 鹅掌楸树高生长拟合数学模型Table 2 The fitting results of tree height growth mathematical model of Liriodendron chinense

表3 鹅掌楸材积生长数学模型拟合结果Table 3 The fitting results of volume growth mathematical model of Liriodendron chinense
3.4 鹅掌楸生长模型验证
采用F检验方法对筛选出的鹅掌楸胸径、树高和材积生长最优模型进行验证,并计算各性状最优数学模型下与实际值的平均偏差、平均绝对偏差、平均相对偏差、平均相对偏差绝对值等指标,以评估模型拟合的效果和精度。由表4 可见,筛选出的鹅掌楸胸径、树高、材积的模型均通过了F值检验(P=0.0001<0.01)。胸径生长模型的平均偏差、平均绝对偏差、平均相对偏差、平均相对偏差绝对值分别为0.0027、0.1353、0.7669%、2.5295%;树高生长的平均偏差、平均绝对偏差、平均相对偏差、平均相对偏差绝对值分别为-0.0026、0.0648、-0.4410%、1.2603%;材积生长的平均偏差、平均绝对偏差、平均相对偏差、平均相对偏差绝对值分别为0.0001、0.0007、-2.1334%、2.6864%。三个模型的预测精度分别为99.7258、99.8827 和99.7930。以1 年为一个龄阶,分别代入鹅掌楸的胸径生长模型D=75.6887{1-e-[(T+2.3354)/19.5656]^3.1489}、树高生长模型H=(55.5498+34.2298T1.9310)/(119.6386+T1.9310)、材积生长模型V=2.5736{1-e-[(T-2.2455)/16.3381]^3.8741},将实测值与预测值进行比较并计算残差(表5)。结果表明,采用这3 个模型分别对鹅掌楸胸径、树高和材积生长进行预测,预测值与实测值之间差异小、预测精度高,表现出极好的拟合效果。说明本研究优选出的生长模型可以较好地拟合鹅掌楸的胸径、树高及材积生长,可用于指导生产实践。为方便生产操作,根据胸径、树高和材积的实测值,计算鹅掌楸的平均生长量和连年生长量,并绘制趋势图(图1),发现除树高的平均生长量和连年生长量在第11年开始交汇外,胸径和材积在第12 年仍处于上升趋势。说明试验地内的鹅掌楸处于树高生长的减缓期和胸径、材积的速生期,宜继续培育获得更大的生长量。

表4 鹅掌楸最优生长模型检验Table 4 Test of the best growth modle of Liriodendron chinense
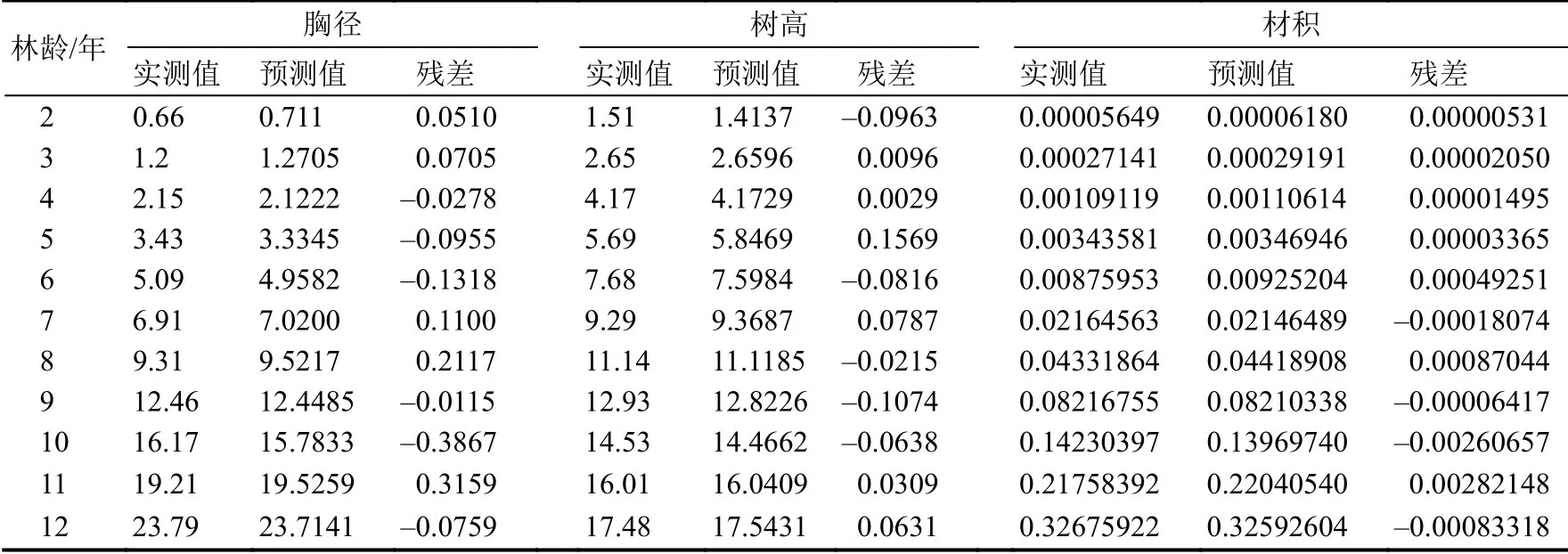
表5 鹅掌楸生长模型实测值与预测值的比较Table 5 Comparison of measured value with predicted value in the growth modle of Liriodendron chinense
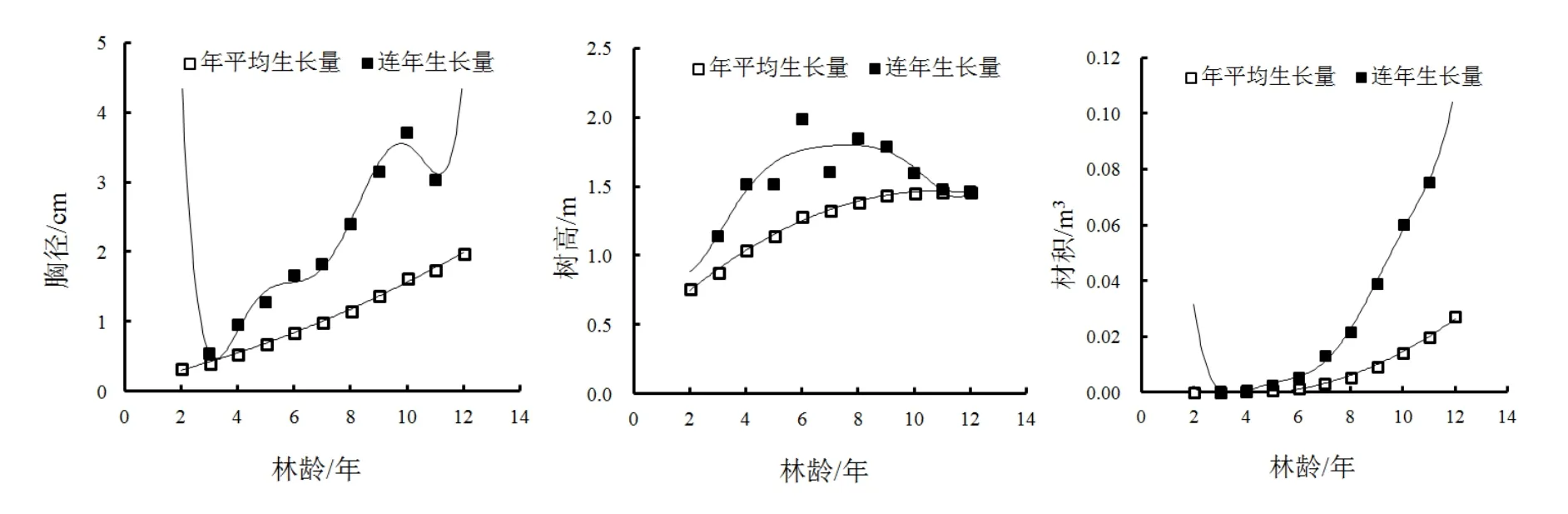
图1 鹅掌楸胸径、树高、材积生长趋势Fig. 1 Trend of DBH, height and volume growth of Liriodendron chinense
4 讨论
在人工林生产经营实践中,选择长势接近平均值的标准株进行树干解析,进而研究胸径、树高和材积生长模型,如果模型拟合性好,不砍树就能较为准确地估计人工林中树体的生长情况,减少人力物力的消耗和对树体的破坏[19]。该方法已用于探讨峦大杉(Cunninghamia konishii)[18]、火力楠(Michelia macclurei)[20]、灰木莲(Manglietia glauce)[21]、川西云杉(Picea likiangensisvar.balfouriana)[22]、侧柏(Platycladus orientalis)[23]、 黧 蒴 栲(Castanopsis fissa)[24]、长白落叶松(Larix olgensis)[25]、麻栎(Quercus acutissima)[26]的生长规律。其中,欧建德等[18]更是通过材积拟合方程计算峦大杉在福建省南平市来舟林场的数量成熟年限为32~34 年,并确定了峦大杉的合理轮伐期为32 年。
本研究在DPS V15.10 数据处理系统中采用Logistic、Webull、二次曲线等13 个有代表性的数学模型对福建省南平市政和县鹅掌楸人工林中标准木的胸径、树高和材积生长逐一进行方程拟合,筛选出鹅掌楸的胸径、树高、材积生长最佳模型,其拟合精度均达99.5%以上,且平均偏差、平均绝对偏差、平均相对偏差、平均相对偏差绝对值较小。各林龄段的生长预测值和实测值相比较,数据吻合度高,残差总体偏小,趋势线表现一致。可以用于指导预测鹅掌楸人工林的生长情况。
本研究中,鹅掌楸胸径以及材积的生长趋势都显示林龄为12 年时鹅掌楸尚处于高速生长阶段,说明样地内的鹅掌楸林分尚未达到成熟年限,应当延长周期继续培育,此时应加强林分抚育管理和补充树体营养,促进早成材成好材。需注意的是,鹅掌楸是对立地条件敏感的树种,在不同地域或不同立地条件下种植的鹅掌楸人工林,运用本研究得出的最优生长模型进行生长预测,可能会存在一定的误差。此外,本试验林分年龄为12 年,尚未达到数量成熟,在时龄更大时或达到数量成熟年龄时,需对本试验林分进行再调查和生长模型研究,以对本研究的最优生长模型进行验证和优化,从而更好地应用于生产。
