基于NSGA-Ⅱ的多目标航班登机口调度研究
2020-03-25文笑雨孙海强王蒙冯士浩
文笑雨,孙海强,王蒙,冯士浩
(郑州轻工业大学 河南省机械装备智能制造重点实验室,河南 郑州 450002)
0 引 言
近几年,由于旅游业的快速发展,民航客运量大幅增加,各大机场相继出现了候机紧张的状况,飞机在登机口调度的不合理性已经成为航班延误的重要原因之一[1]。为了适应未来的发展,解决登机口的调度问题,机场往往都会新建候机楼或扩大候机楼的面积,随之登机口的数量也会相应增加。虽然增加登机口可以缓解候机紧张的压力,但是对中转旅客的航班衔接具有一定的影响,这增加了中转旅客步行时间,削弱了民航运输的便捷程度[2],因此,减少中转旅客的步行时间对于机场管理具有非常重要的意义。
仅考虑登机口分配的航班-登机口的优化分配问题已经被很好地解决了[3],在登机口调度过程中考虑减少中转旅客的步行时间,属于多目标下的优化调度问题。近年来,多目标登机口的调度问题逐渐成为了研究热点。A.Drexl 等[4]进一步讨论H.Ding等[5]的模型,模型中考虑了航空公司对登机口的偏好,建立了多目标优化数学模型,最后通过帕累托模拟退火算法求解;B.Maharjan 等[6]建立了登机口网络流优化模型,以最小化飞机在机场地面的航空燃油费用和总的乘客不满意度为优化目标进行优化;U.Dorndorf 等[7]考虑了登机可用性约束建立模型,并设计启发式算法分阶段求解;TANG C H等[8]将航班偏好作为优化目标的主要影响因素进行了分析研究;王志清等[2]在图论的基础上建立了登机口的网络模型,提出了该模型在使用中的实用算法,其结果缩短了旅客步行距离,提高了设施利用率;WU D等[9]提出了以最小化乘客步行距离和最小化各登机口被使用量为优化目标的多目标优化模型,设计了一种基于蚁群协同策略和信息素更新策略的改进蚁群优化算法(ICQACO)求解。由上述文献可知,针对优化分配登机口的同时考虑最小化旅客总步行时间的研究仍很有限。因此,本文针对多目标航班登机口调度问题开展了研究,以最小化登机口总使用量、最小化旅客总步行时间为优化目标,设计了这两个优化目标的函数,提出基于NSGA-Ⅱ算法求解,以快速非支配排序及拥挤距离为适应度评价方法,根据柔性作业车间调度问题与航班登机口调度问题的共性特点进行类比,提出一种问题假设与数据处理方法,采用基于工序、基于加工机器分配的两部分编码方法,最后通过对实例的求解,验证所建立数学模型和设计算法的有效性。
1 多目标航班登机口调度模型
1.1 问题描述
多目标航班登机口调度问题的描述如下:某机场共有m个可用登机口,其中国际厅T拥有r个登机口(可停靠任意航班且具有出入境功能),国内厅S 拥有k个登机口(仅可停靠飞往国内的航班),国际厅T与国内厅S之间存在一段距离,如图1所示,对于中转旅客需步行一段路程。已知n个航班在登机口上的启用与停用时间。本文的调度目标是在上述已知条件下确定各个航班的登机口位置、确定登机口各个航班停靠顺序,使得多种性能指标得到兼顾,从而确定一组均衡解。
为了形象描述多目标航班登机口调度问题,以9个航班的停靠信息为例(表1),该机场有5个登机口,其中T厅2个(M1,M2),S厅3个(M3,M4,M5),则9个航班5个登机口的调度问题求解包括两部分:确定9个航班的登机口;确定5个登机口当天所有航班的停靠顺序。表2给出了该问题的一种求解结果。
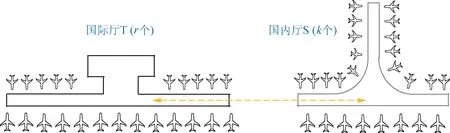
图1 国际厅与国内厅位置示意图
Fig.1 Schematic diagram of the international and domestic offices
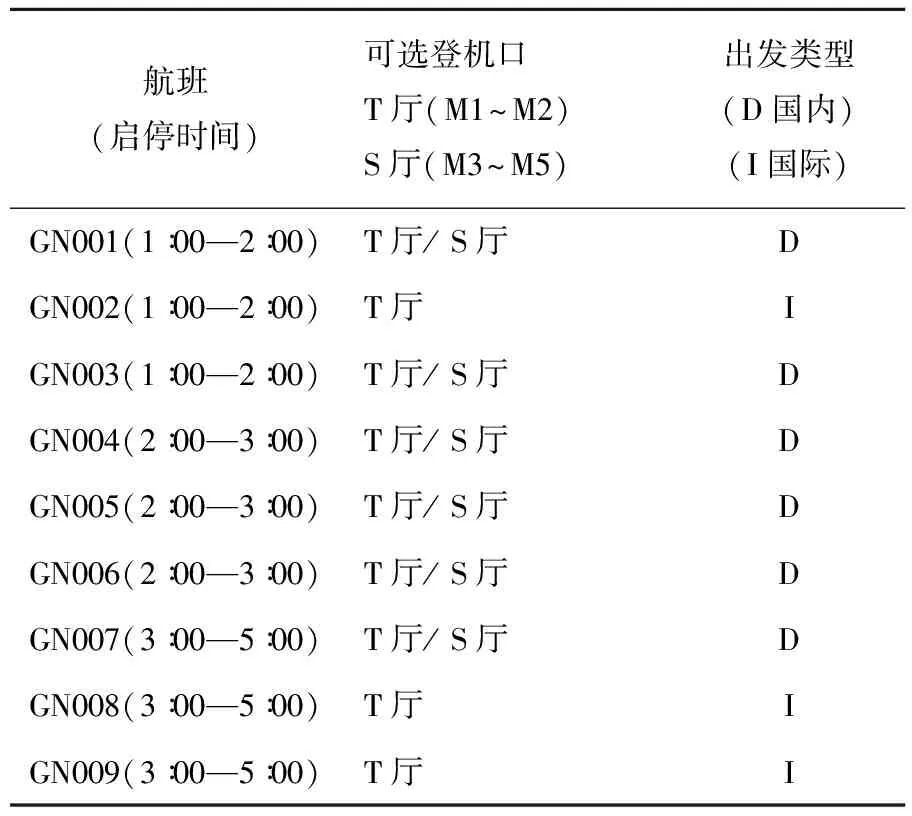
表1 9个航班的停靠信息

表2 9个航班5个登机口调度问题的求解结果
1.2 数学模型
针对多目标航班登机口调度问题,本文以最小化登机口总使用量和最小化旅客最大总步行时间为性能指标,建立如下条件假设:
(1)同一登机口同一时刻只能停靠一架飞机。
(2)不论S厅还是T厅登机口停靠的飞机必须在同一登机口出发。
(3)航班在各个登机口的启用与停用时间已知且相同。
这两种性能指标的目标函数定义如下。
(1)f1:最小化登机口总使用量(sum)

(1)
(2)f2:最小化旅客最大总步行时间(Tp)
minTp={maxPTj,j=1,…,m},
(2)

pnj,k为j登机口k航班的中转人数;twalk步行时间;PTj为j登机口所有航班的总步行时间。
决策变量包括登机口的选择决策xk,r、登机口航班的排序决策yj,k,k′以及中转旅客步行时间的决策Ωj,k。
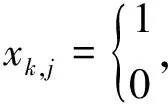
(3)
式中,xk,j=1 时为k航班在j登机口停靠,xk,j=0时为k航班不停靠在j登机口。

(4)
式中,yj,k,k′=1时为j登机口k航班在k′航班之前停靠,yj,k,k′=0时为j登机口k航班在k′航班之后停靠。

(5)
式中:Ωj,k=1时为j登机口的k航班不是T厅到达T厅出发,即k航班的中转旅客需要一定的步行时间,Ωj,k=0时为j登机口的k航班是T厅到达T厅出发,k航班上的中转旅客不需要步行。
S.T.同一登机口各航班的停靠时间顺序约束
(Cj,k-Cj,k′-tj,k)×xk,j×xk′,j×yj,k,k′≥0, (6)
式中:Cj,k,Cj,k′为j登机口k航班和k′航班的出发时间;tj,k为j登机口k航班的停靠时长。
每个航班仅能选择一个登机口停靠

(7)
式中,Mk为k航班可停靠的登机口集合。
1.3 问题假设与数据处理
柔性作业车间调度问题中每个工件包含多道工序,调度目标是为每道工序选择最合适的加工机器、确定每台机器上各工件工序的最佳加工顺序及开完工时间,对于航班登机口调度问题,各航班的到达、出发时间是预先确定的(工件的开完工时间已确定),调度的目标是确定每个航班最合适的登机口(每道工序选择最合适的加工机器)、确定每个登机口当天停靠飞机的最佳顺序(每台机器上各工件的加工顺序)。由于航班登机口调度与柔性作业车间调度存在一些共性特点,因此本文将航班登机口调度问题与柔性作业车间调度问题进行类比,并做出如下问题假设:
(1)各航班的到达、出发时间是预先确定的,基于此可将停靠时间段互不交叉的航班假设为同一工件中的不同工序,将停靠时间段发生冲突的航班假设为不同工件的工序。
(2)每个登机口同一时间段内只能停靠一架航班,类似于每台机器上同一时间仅能加工一个工件,故将所有的登机口设为各个工件的加工机器。
以表1中9个航班的停靠信息为例,根据问题假设,对9个航班进行随机分配,确定各个航班的工件号,按照时间的先后顺序对归属于各个工件的航班进行排列,确定各个航班的工序号,如表4所示。
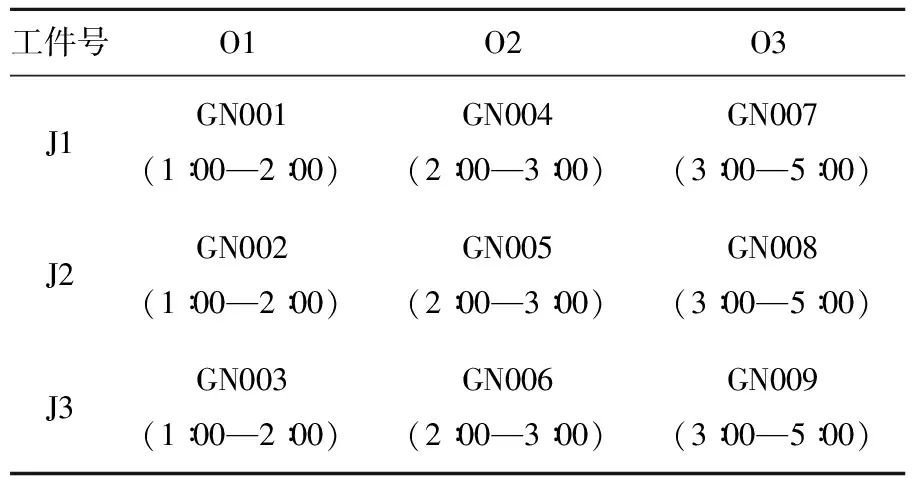
表4 9个航班的工件归属信息
2 基于NSGA-Ⅱ求解的多目标航班登机口调度问题
NSGA-Ⅱ(A Non-dominated Sorting Genetic Algorithm-II)算法是WU D等[9]于 2000 年在 NSGA 的基础上提出的。它是目前最流行的多目标优化算法之一,广泛应用于诸多组合优化问题。该算法可同时兼顾多个优化目标。
2.1 编码、解码与初始化
对于多目标航班登机口调度,编码由两部分组成:第一部分采用基于工序的编码方法[10];第二部分采用基于机器分配的编码方法[11]。具体编码操作如下。
(1)基于工序的编码。该编码方法是以染色体基因序列中某工件号的出现次数定义该工件待加工的工序号,染色体基因的个数为所有工件的工序的总数,即当日航班总数。表4给出了9个航班的工件归属信息,设表5的1条染色体基因序列为[1 2 1 2 3 2 3 1 3],该染色体共有9个基因,其中3个1依次代表着归属于工件J1的3个航班分别为O1(GN001)、O2(GN004)、O3(GN007),染色体中2,3为归属于工件J2、J3的航班。
(2)基于机器分配的编码。基于机器分配编码的基因序列长度为工序总数l(当日航班总数),分别用工序号1,2,…,l表示。根据l道工序形成了l个可选机器的子集{S1,S2,…,Si,…,Sl},Si为第i个工序的加工机器集合,即第i个航班登机口集合,表示为{m1i,m2i,…,mni},Si中每个元素均为登机口。
基于机器分配编码的基因序列表示为[g1,g2,…,gi,…,gl],gi为集合Si中的第gi个登机口mgi。以表4工件归属信息为例,染色体基因序列[1 2 1 2 3 2 3 1 3]中的第二个基因2代表着归属于工件J2的航班O1(GN002)。由表1可知,该航班拥有两个登机口S2={1,2},若设机器基因序列[2 1 2 1 2 1 2 1 3],则g2=1,可确定航班O1(GN002)的登机口为S2中的第1个登机口M1,以此类推,可确定染色体序列中各个航班的登机口,如图2所示。
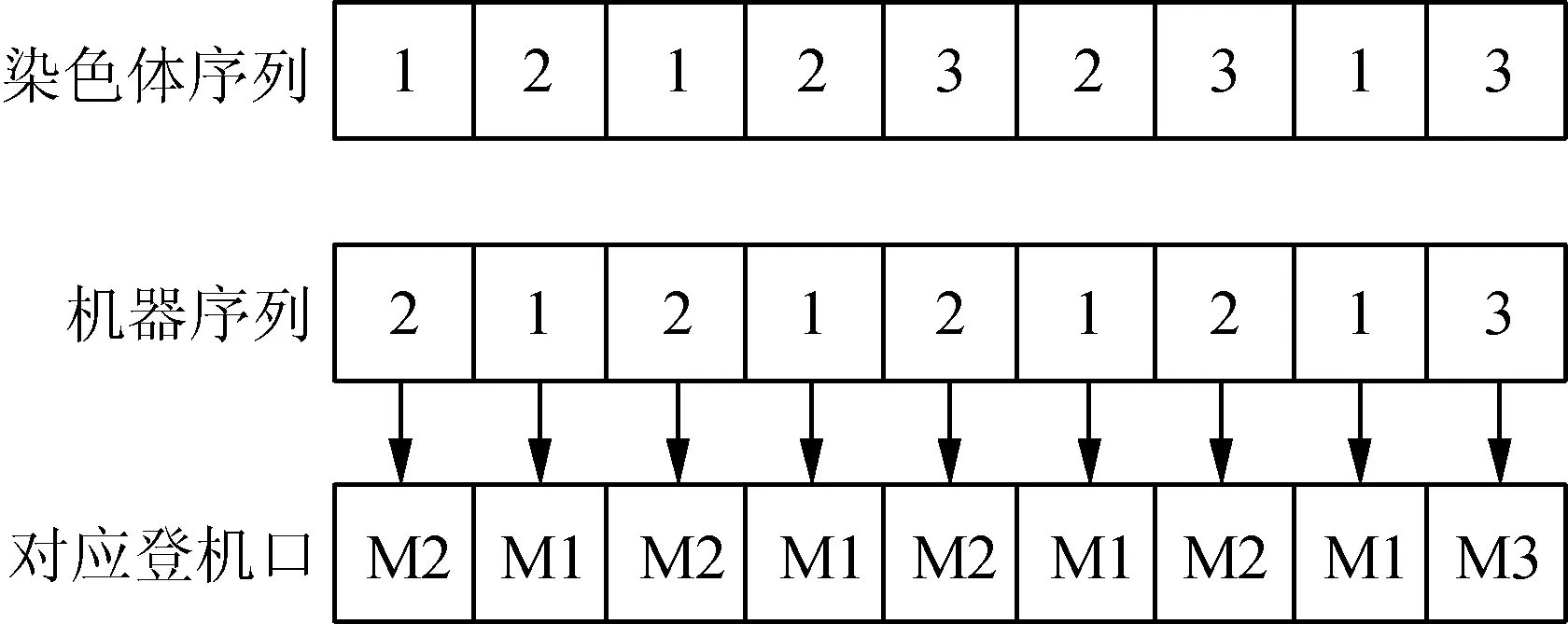
图2 基于机器分配编码的解码过程
基于机器分配编码的机器序列确定各个航班的登机口为解码第一步,第二步按基于工序编码的染色体序列确定登机口各个航班的停靠顺序,从而完成整个解码过程。本文在解码过程中又引入了插入式贪婪算法[12],增加登机口停靠的航班,减少登机口的总使用量。
NSGA-Ⅱ算法种群中每个个体都代表着一种可行的调度方案,按照上述的编码方法,每个个体都包含两段序列(染色体序列、加工机器序列),均采用随机初始化的方法生成基因序列,若加工机器序列中存在不满足约束要求的基因,则对该基因进行随机更换,直到满足约束要求为止,最终通过解码操作确定各个航班停靠的登机口、登机口各个航班的停靠顺序。
2.2 适应度评价
适应度反映了个体适应环境的能力,适应度好的个体将有更多的机会遗传到下一代。本文采用NSGA-Ⅱ中的快速非支配排序、拥挤距离作为评价方法比较种群个体的优劣[13]。种群中非支配等级低的个体的适应度优于非支配等级高的个体,对于同一等级中的个体,拥挤距离大的个体具有更好的适应度值。
2.3 基于NSGA-Ⅱ算法求解的总流程
本文提出基于NSGA-Ⅱ算法求解的多目标航班登机口的优化调度问题的详细步骤如下。
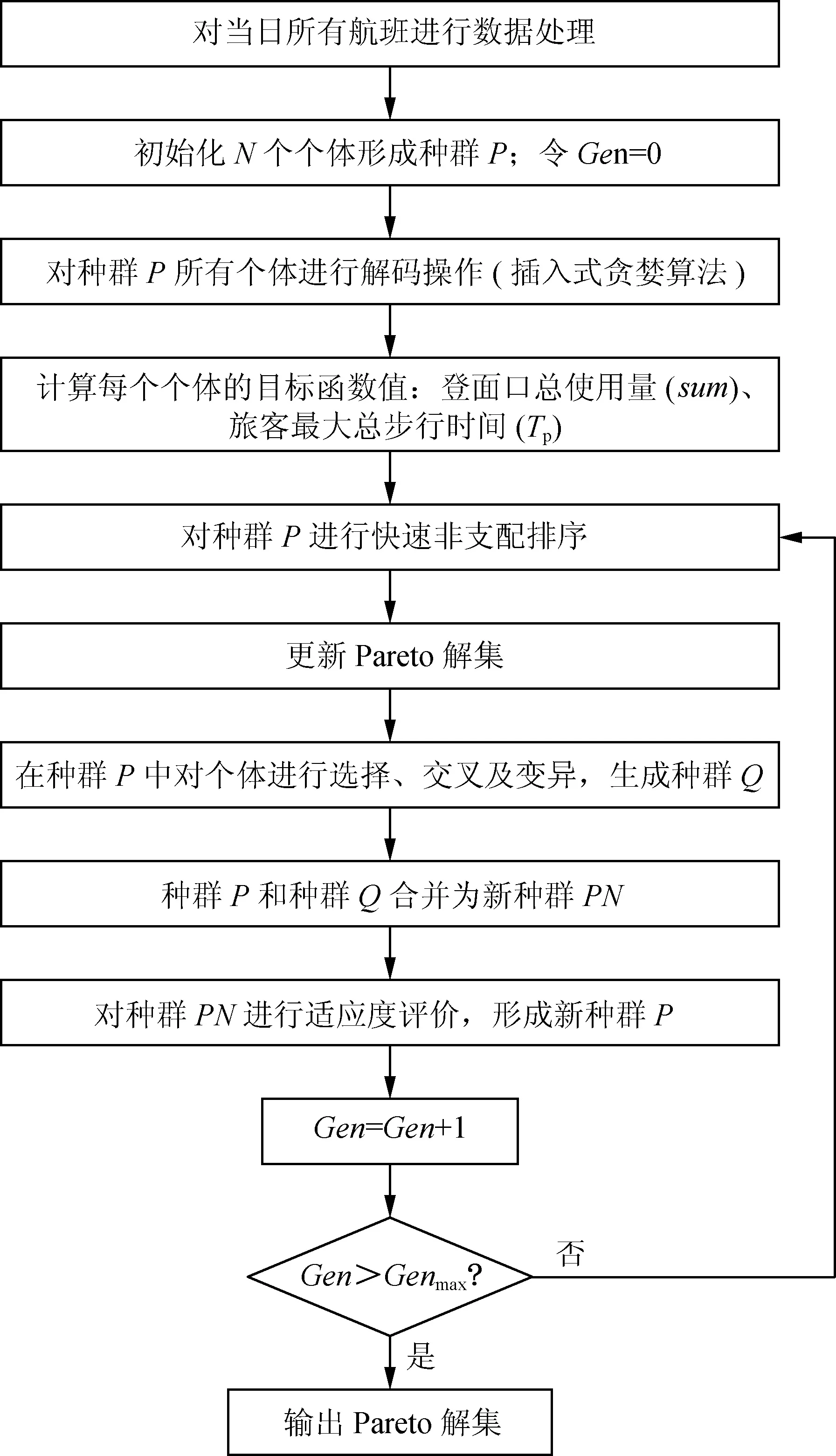
图3 基于NSGA-Ⅱ算法求解的总流程
步骤1 设定NSGA-Ⅱ算法的参数:算法迭代次数Genmax,种群数目N,选择概率Ps,交叉概率Pc,变异概率Pm,Pareto解集最大数目MaxSize。
步骤2 对当日所有的航班进行数据处理,确定所有航班的工件号、工序号。
步骤3 初始化N个个体,形成父代种群P;令Gen=0。
步骤4 对种群P中的每个个体采用基于插入式贪婪算法的解码操作,解码后计算登机口总使用量(sum)、旅客最大总步行时间(Tp)。
步骤5 根据个体的评价值,对种群P的所有个体进行快速非支配排序及拥挤距离计算,每个个体拥有两个属性,即非支配等级和拥挤距离。
步骤6 更新Pareto解集。
步骤6.1 如果当前Pareto解集为空时,将当前种群中非支配等级为1的个体(irank=1)存入Pareto解集;如果当前种群P中irank=1的个体数目大于MaxSize,按照拥挤距离从大到小依次填入Pareto解集中。
步骤6.2 如果当前Pareto解集不为空时,在种群P中剔除与当前Pareto解集中相同的个体,将剔除后种群P中irank=1的个体和Pareto解集中的个体存入种群Ptemp中,对种群Ptemp进行快速非支配排序及拥挤距离计算,如果种群Ptemp中irank=1的个体数目大于Pareto解集MaxSize,按照拥挤距离依次填入Pareto解集中,否则直接将irank=1的个体存入Pareto解集。
步骤7 依据锦标赛选择法,优先选择非支配等级低的个体染色体,相同等级下选择拥挤距离大的个体,对种群P中的前M个个体进行选择;采用文献[12]的操作分别对种群P中其他个体的染色体序列、机器序列进行交叉和变异操作,生成新种群P。
步骤8 去除种群P中与种群P中相同的个体,将种群P个体和种群P个体合并为种群PN。
步骤9 根据种群PN中个体适应度值,选择N个个体,形成种群P。

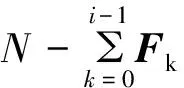
步骤10 令Gen=Gen+1,如果Gen>Genmax,输出Pareto解集,否则跳转到步骤5。
3 实例验证
3.1 实例信息
以某机场当日51个航班15个登机口调度问题为例,对本文中的数学模型及求解算法进行验证。通过数据处理,得到了51个航班的工件归属及停靠信息,如表5所示。
表6为登机口分布情况,根据表5 中各航班的出发类型,可知各航班停靠的登机口范围,表7为中转旅客在各厅之间步行时间。

表5 51个航班的工件归属及停靠信息
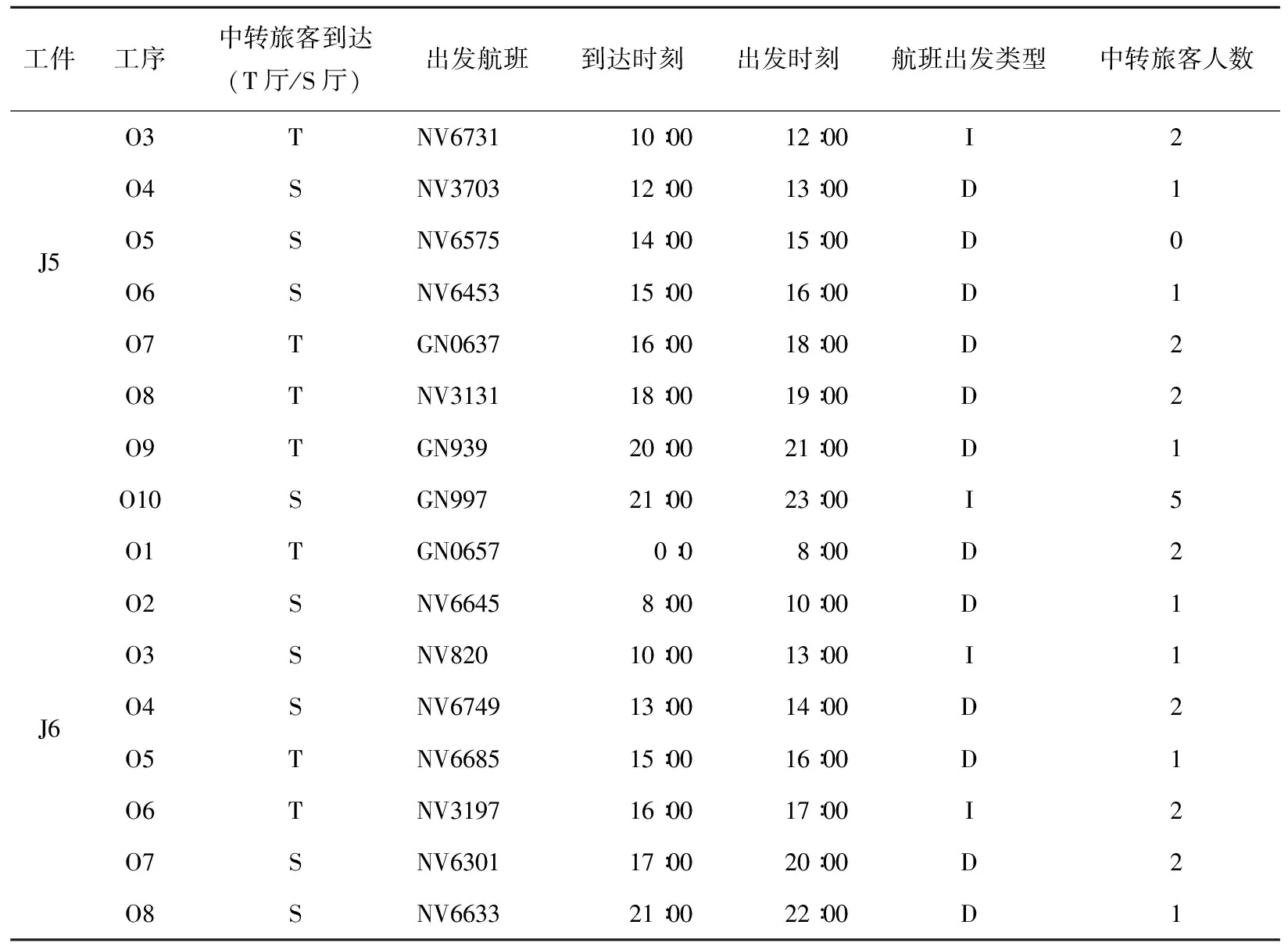
续表5

表6 登机口分布情况
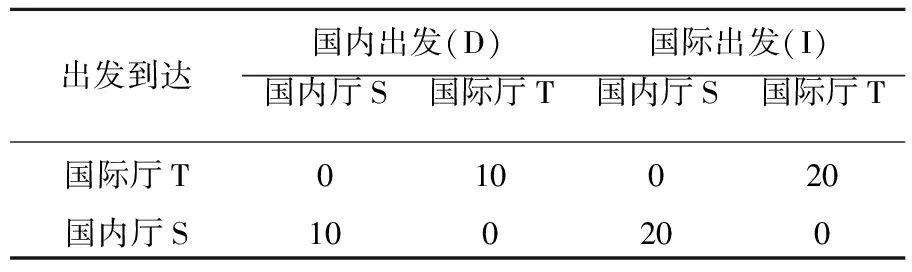
表7 各厅之间的中转时间
3.2 计算结果与分析
针对多目标航班登机口调度问题,使用Visual C++进行编程,计算机型号Intel(R)Core(TM)i5-7400 CPU @ 3.00 GHz,4.00 G运行内存,算法参数设置如表7所示。

表7 参数设置
使用提出的NSGA-Ⅱ算法,求解独立运行20次得到一组 Pareto解集,如表8所示。
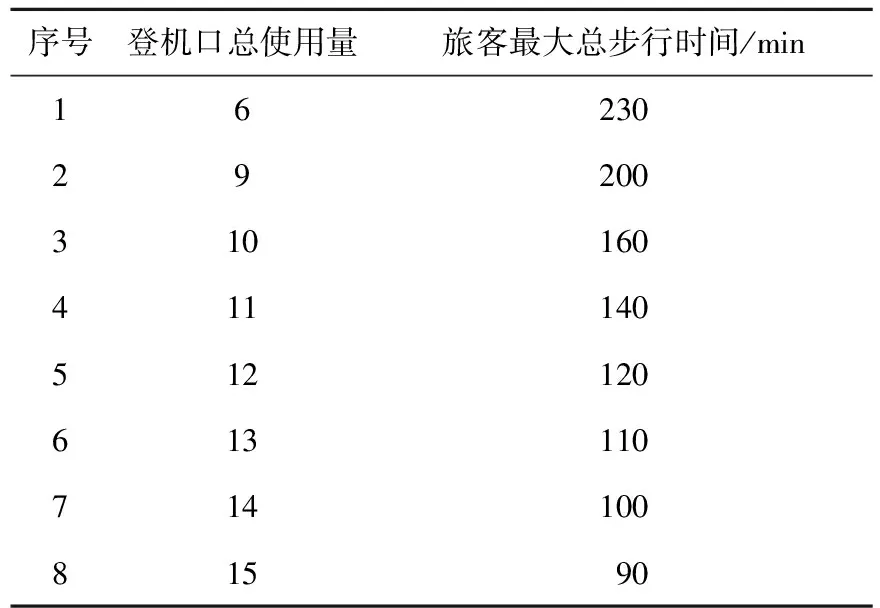
表8 Pareto解集
从表8可以清楚看出,随着登机口总使用量的增加,各登机口的旅客最大总步行时间不断减小,这说明这两个优化目标是矛盾的。为了进一步说明两优化目标之间的矛盾关系,按登机口总使用量的增序排列了各个Pareto解,如图4所示。由图4可见,登机口的总使用量和旅客最大总步行时间并非线性关系,如果仅仅采用单目标优化算法求解,则无法兼顾两个目标。使用本文提出的NSGA-Ⅱ算法求解,以快速非支配排序及拥挤距离计算为评价方法,可以最终确定一组Pareto解集,该解集中的每个解都能够兼顾这两个优化目标,登机口的调度员可以根据机场的当日情况选择合理调度方案,以节省登机口的使用量或旅客的步行时间。图5给出了序号8解的航班调度图,该解为登机口旅客总步行时间最小的解,图5中的J1.1表示归属于工件1的第一个航班,即NV675(5∶00—7∶00)在登机口1停靠,其他的类同。

图4 Pareto解集中各均衡解的分布
图6为序号8解各登机口的航班量,图7 为该解各登机口的旅客总步行时间。
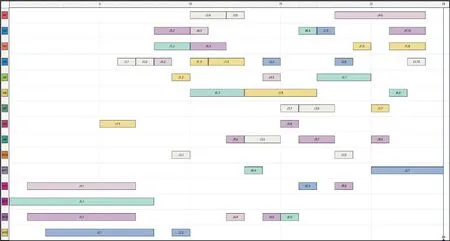
图5 Pt 最小解的航班调度图

图6 各登机口的航班量

图7 各登机口旅客的总步行时间
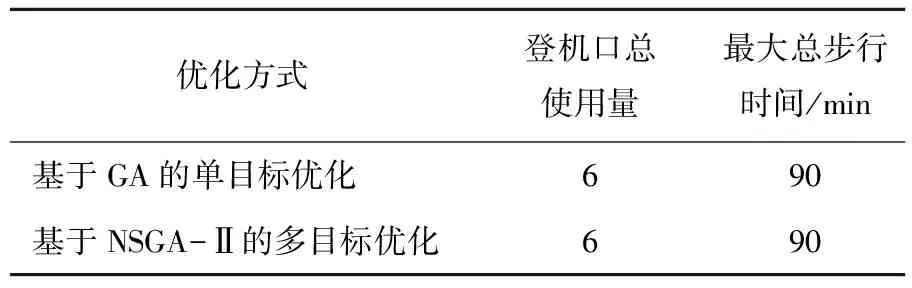
表9 各优化目标的最小值
为了验证NSGA-Ⅱ算法对于单个目标函数的优化,本文使用遗传算法(GA)分别对这两个优化目标进行求解,求解结果如表9所示。由表9可知,本文采用NSGA-Ⅱ算法求得的Pareto解集包含了单目标优化时的最小值。对于单个目标函数的优化,NSGA-Ⅱ算法的优化效果比基于GA的优化结果好。
4 结 论
针对多目标航班登机口的调度问题,建立了以登机口总使用量最小、旅客最大总步行时间最小为优化目标的多目标数学模型,设计了登机口总使用量、旅客最大总步行时间的目标函数,并基于NSGA-Ⅱ算法求解。根据柔性作业车间调度问题与航班登机口调度问题的共性特点进行类比,提出了一种问题假设与数据处理方法,有效地将所有的航班变换成各工件的工序,将各个登机口变换成加工机器,结合类比的问题采用基于工序的编码方法、基于机器分配的编码方法,最后通过对某机场51个航班15个登机口的调度问题进行求解,验证了所建立模型和提出算法的可行性。该研究有助于推动运筹学技术在机场登机口管理中的应用,为机场管理者提供决策依据,同时也提高机场的服务质量。
