气体阀门内漏声发射评价参量研究及其应用
2020-03-23龙飞飞刘永轩
龙飞飞,刘永轩,王 琼,李 伟
(1. 大连民族大学机电工程学院,辽宁大连116600;2. 东北石油大学机械科学与工程学院,黑龙江大庆163318;3. 中国石油化工股份有限公司青岛安全工程研究院,山东青岛266071)
0 引 言
在石油、石化行业的过程装置中,阀门是必不可少的一部分,在此行业中,一直对阀门保持较高的使用率。在生产过程中,阀内介质大多为腐蚀性、有毒、易燃、易爆介质,阀门泄漏引发的事故时有发生,且绝大部分阀门泄漏难以及时发现,不但对生产、环境造成严重影响,更会导致重大安全事故。因此,阀门泄漏检测和泄漏量估算在阀门寿命预测、提高阀门安全性能方面具有重要意义[1]。
自19 世纪60 年代开始,国外关于阀门内漏的研究就已展开,研究发现,在众多检测手段中,声发射技术在阀门内漏检测领域表现优异。2005 年,韩国国立大学的Lee 等[2]将声发射技术应用于核电站止回阀泄漏故障检测。2007 年,Puttmer 等[3]实现了调节阀泄漏的声发射在线检测。2010 年,Kaewwaewnoi 等[4]经过理论和实验研究,提出了声发射特征参量与阀门内漏率之间的数学模型。2011年Jirarungsatian 等[5]进行了阀门内漏模拟实验,并研制出具有内漏率估算功能的气体介质阀门检测仪。2012 年,Meland 等[6]对常用阀门内漏检测方法进行了总结,并提出两种检测方法,其中一种为基于数据处理的检测方法,另一种为基于声发射特征参量与物理参数的数学模型的方法。国内自20 世纪70 年代初就已对声发射技术展开研究,在阀门泄漏检测方面的应用研究开始于20 世纪90 年代。1996年,东北电力大学孙伟等[7]采用声发射技术对阀门泄漏检测进行了研究,开发出用于阀门内漏诊断的声发射检测仪。2003 年,大庆石油学院戴光等[8]采用声发射技术对承压阀门泄漏进行了检测,提出声发射信号幅值与泄漏率二者对数存在线性关系,为阀门泄漏的定量诊断提供了指导。2006 年,王永涛等[9]从流体角度对阀门泄漏率与声发射特征参数的关系进行了研究,并开发出便携式阀门内漏声学检测仪,实现了阀门微小泄漏的检测。2008 年,大连工业大学李明霞等[10]通过提取阀门泄漏声信号(Mel-scale Frequency Cepstral Coefficients,MFCC)特征参数,对阀门泄漏进行有效诊断,实现了阀门泄漏的预警。2017 年,东北石油大学李伟等[11]根据Parseval 原理研究了阀门泄漏率对声发射参数的影响,提出在阀门泄漏检测中,与其他参量相比,声发射均方根电压(Root Mean Square,RMS)具有更高灵敏度。国内研究人员还针对阀门在不同条件下的泄漏提出了处理和预防措施。虽然国内关于阀门内漏的基础理论已经取得较大成果,但大多基于传统声发射参量与阀门内漏率的关系,关于阀门内漏声发射评价参量的研究少之又少。
由于传统声发射的评价参量的误差较大,不能满足工程应用需要,研究成果不能付诸工程实践。为降低评价参量误差、满足工程应用要求,本文提出了一种新的声发射参量对阀门内漏进行定量评价,并提出基于新参量的阀门内漏评价模型,进行阀门内漏模拟实验。采用新声发射参量对实验阀门内漏进行评价,验证了新声发射参量的可行性以及评价精确度,可为提高阀门内漏率声发射评价准确性、将声发射技术应用于阀门内漏工程监测提供指导。
1 声发射评价参量研究
目前声发射检测评价常采用的声发射特征参量有幅度、能量、计数、事件、上升时间、持续时间等,同时还包括表征波形特征的中心频率、核心频率等。因此,要对阀门内漏进行声发射评价,首先要确定用于阀门内漏评价的最佳声发射参量,该参量应具备以下性质:
(1) 对阀门内漏率变化比较敏感,或者能够随内漏率的变化呈现一定的趋势和规律;
(2) 对同一类型的阀门应具有普遍适用性,即对同一类型、不同尺寸的阀门均可用同一参量进行评价,或者任意类型的阀门内漏均可采用此参量进行评价;
(3) 内漏率之外的因素如气压、温度等,对该参量的影响不大;
(4) 对电子噪声、机械噪声等外界干扰具有一定的免疫能力,即抗干扰能力较强。
阀门内漏信号为连续性信号,在已知的声发射参数中,常用于连续型信号评价的声发射参量有平均信号电平(Average Signal Level, ASL)、均方根电压(RMS)等。本文基于实验数据,就ASL、RMS 在阀门内漏声发射评价中的表现与本文提出平均声发射能量进行比较,以期确定最佳评价参量。
采样时间内所获得的声发射实验数据S 包含m个撞击信号,撞击信号采样点数为 n,即S=记,记为,则均方根电压RMS、平均信号电平ASL 表示为

式中:GPre为前置放大器增益值,单位dB;i、j 分别为采样点序号、撞击信号序号;Vref=1 µV,为参考电压。
式(1)、(2)中,LAS、VRMS根据单一撞击信号计算得到,其中VRMS针对采样周期内信号进行平均,能准确反应当前信号波动,而LAS通过对数运算对参数变化进行压缩,能够更好地反映当前信号的强度。然而LAS、VRMS只能反映单一撞击信号所包含的信息,不能完整体现实验数据信息,无法对不同内漏情况下全过程声发射信号进行对比和评价。在以往研究中,往往在众多撞击信号中挑选单一撞击信号计算LAS、VRMS等参数,并在不同实验之间进行比较,进而得到声发射参数随内漏率变化的规律。然而,无论以什么原则挑选,单一撞击信号不能充分体现一段采样时间内实验数据所包含的信息,很容易造成信息遗漏,因此本文构造出新的声发射参量,该参量以VRMS参量为基础对实验信号能量进行计算,同时采用对数和平均算法,算法覆盖范围从单一撞击信号扩展至整个采样时间内所有撞击信号,兼顾了信号的连续性和能量,所构造参量表达算法如式(3)所示:

式中,m 为撞击信号数。
2 实验研究
2.1 实验设置及方案
为验证ERMS,A参量的实用性,用阀门内漏模拟实验装置对不同类型、尺寸的阀门以不同压力进行实验研究,模拟实验数据如表1 所示,实验采用的阀门尺寸基本涵盖了工业常用阀门尺寸、类型。
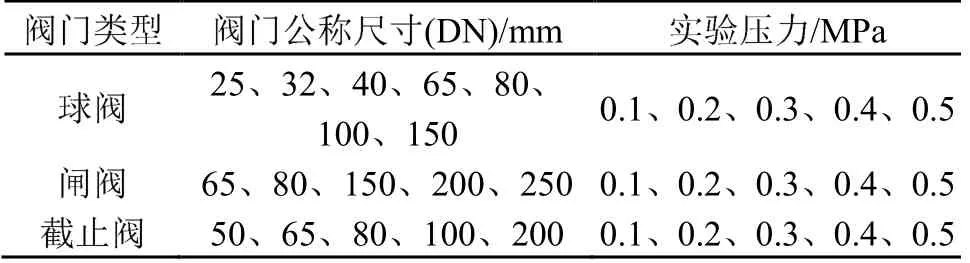
表1 阀门内漏模拟实验内容Table 1 Contents of simulation experiment on valve inner leakage
实验系统主要由阀门内漏模拟系统以及声发射采集系统两部分组成,如图1 所示。

图1 阀门内漏模拟实验检测系统Fig.1 The simulation testing system for valve inner leakage
通过调节阀门开度模拟阀门内漏并控制内漏率,并采用数字流量计测定,在内漏率分别为4、8、12、16、20、24 L·min-1时,在一定时间内采集实验数据。
声发射采集系统主要由传感器、前置放大器、声发射数字采集卡以及声发射分析软件四部分组成。传感器采用R3a 传感器,前置放大器选用2/4/6型前置放大器,可选增益为:20、40、60 dB,采用PCI-II 声发射采集卡以及AEwin 软件对实验信号进行采集、处理。实验中采样频率为1 MHz,采样长度为2 000 个采样点,前置放大器增益为40 dB。
2.2 实验结果分析
本文所有试验均采用相同实验设置对不同阀门进行实验,数据分析结果表明,不同阀门实验数据具有的相同规律,且相同阀门的泄漏信号峰值频率分布范围相似,即相同阀门泄漏信号的频率特性一致,故本文以DN65 闸阀为例进行数据处理。
对采样时间内所有撞击信号进行傅里叶分析,定位各撞击信号频谱峰值频率,统计其最大、最小峰值频率,进而确定实验数据峰值频率的分布,所有撞击信号均包含在该频率分布范围内。不同实验压力下DN65 闸阀内漏信号峰值频率分布如表2 所示。

表2 实验数据峰值频率分布Table 2 Peak frequency distribution of experimental data
为降低实验噪声对信号分析结果影响,对实验信号进行小波包分解,以达到消噪的目的。实验信号主要成分为阀门内漏信号,与噪声相比信号幅值较高,因此可以认为表2 所给出的峰值频率分布即阀门内漏信号的频率分布。
根据傅里叶分析结果,本文采用Sym6 小波对实验数据进行小波包分解、重构,基于平均声发射能量算法,采用MATLAB 软件重新计算生成声发射参量(ERMS,A、VRMS)。根据最大幅值原则,本文将每个实验数据内VRMS最大值与该实验数据重新生成的ERMSA值进行对比,得到重构信号随内漏率的变化曲线如图2 所示,图2 中横坐标Q 表示内漏率。
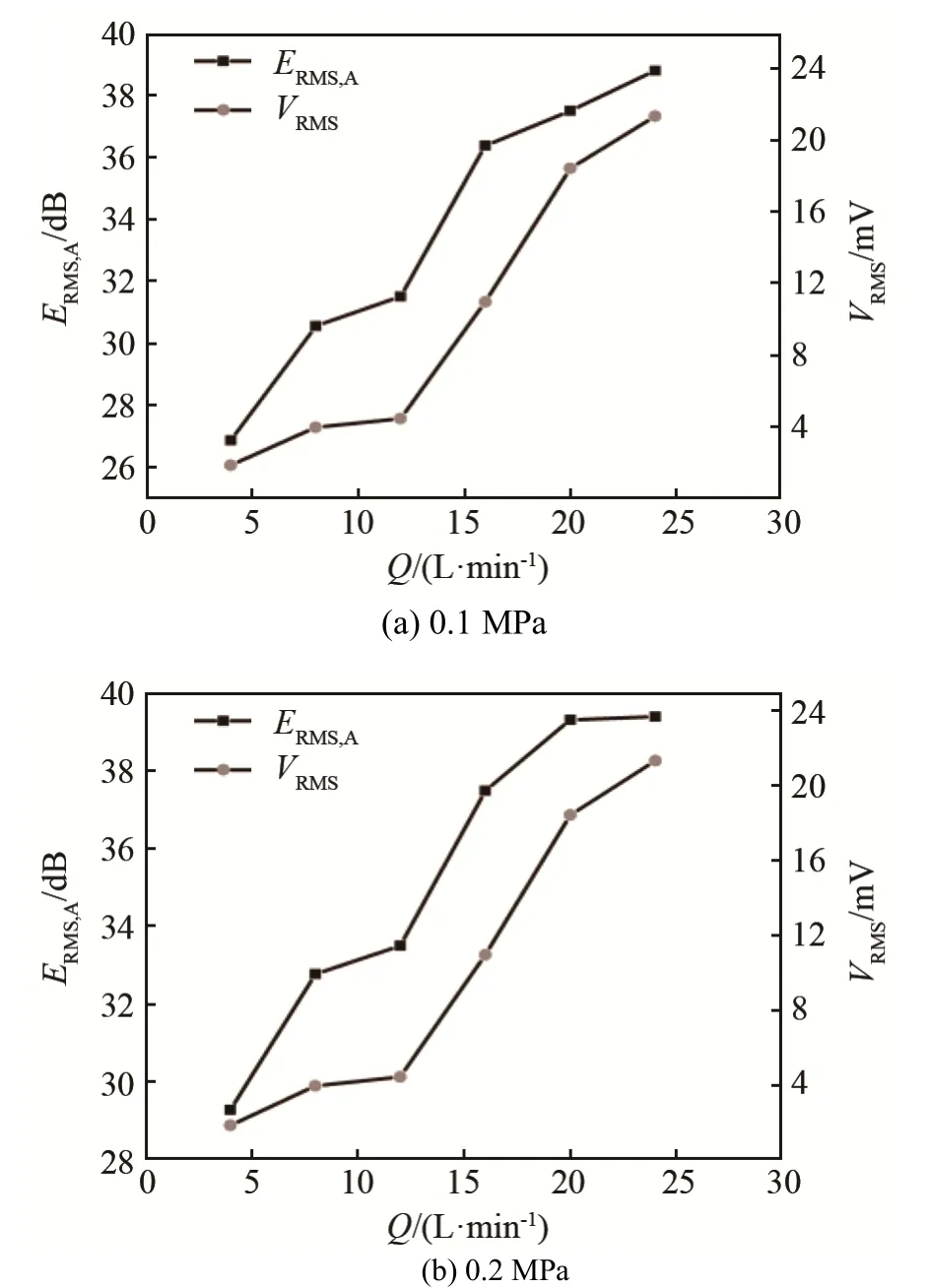
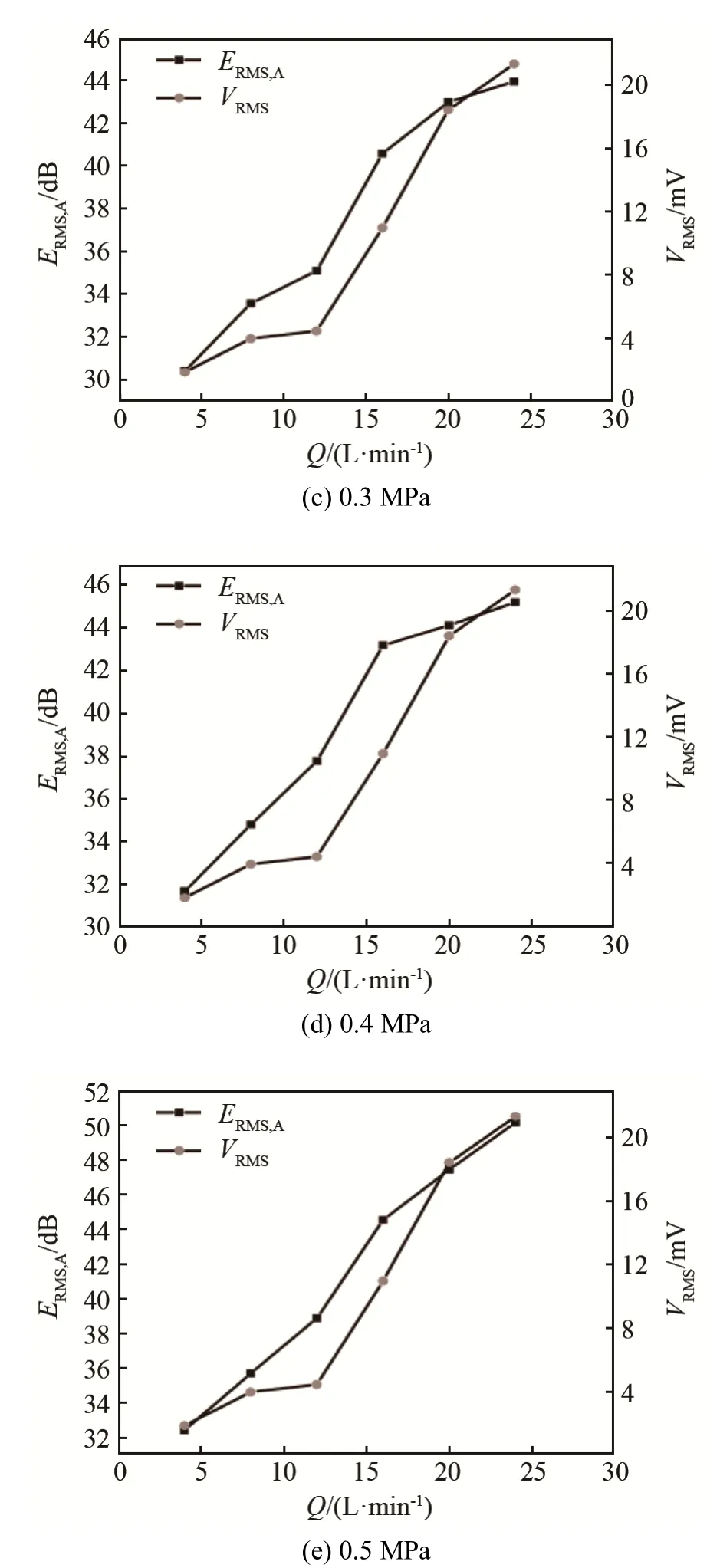
图2 不同内漏压力下ERMS,A和VRMS 随内漏率Q 变化曲线Fig.2 Variation curves of ERMS,A and of VRMS with inner leakage flow rate Q under different pressures
如图2 所示,ERMS,A曲线光滑度明显优于VRMS曲线,更有利于拟合实验数据和分析数据变化规律。近年来研究表明[11-13],声发射参量随阀门内漏率的增加而增加,且二者对数存在线性关系,经过研究,VRMS曲线与ERMS,A曲线相比,对已知模型的拟合方差较大,评价效果较差。
对不同压力下ERMS,A曲线进行横向比较,结果如图3 所示。
对图中5 条曲线进行拟合,所有函数均符合lg Q = a lg ERMS,A+ b 模型,其中a、b 为拟合系数,各条曲线拟合确定系数(R-square)均大于0.9。以0.5 MPa 的实验数据为例, 拟合函数为lg Q =2.825lg ERMS,A- 3 .408, 此 时 R-square 为0.9502。因此,所研究的新声发射参量ERMS,A可以应用于企业阀门的监测。

图3 不同压力下ERMS,A随内漏率Q 变化曲线Fig.3 Variation curves of ERMS,A with inner leakage flow rate Q under different pressures
3 声发射参量应用研究
为验证平均声发射能量的评价效果,采用2.1节的实验系统和实验参数,对DN50 球阀进行阀门内漏模拟实验,实验压力为0.5 MPa。对实验数据做傅里叶变换,得到各压力下实验信号的峰值频率分布,并确定实验数据对应的小波包分解节点如表3 所示。

表3 DN50 球阀实验数据峰值频率分布Table 3 Peak frequency distribution of the experimental data for DN50 ball valve
根据傅里叶分析结果,对实验数据以Sym6 小波进行小波包分解,并在节点<4,0>处重构信号,得到重构信号的ERMS,A值以及VRMS最大值(如无说明,以下均记为VRMS,max),列于表4。
根据GB/T4213-92 规定,DN50 球阀微小泄漏、小泄漏、中等泄漏流量分别为0~39、39~390、390~1 950 L·min-1,在三个泄漏等级内分别挑选6#、10#、12#数据作为实验验证数据,其他数据作为拟合数据进行拟合。根据阀门泄漏发声机理微小泄漏与小泄漏、中等泄漏及更高泄漏的发声机理不同,故本文对ERMS,A-Q、VRMS,max-Q 进行分段拟合,结果如公式(4)、(5)所示:
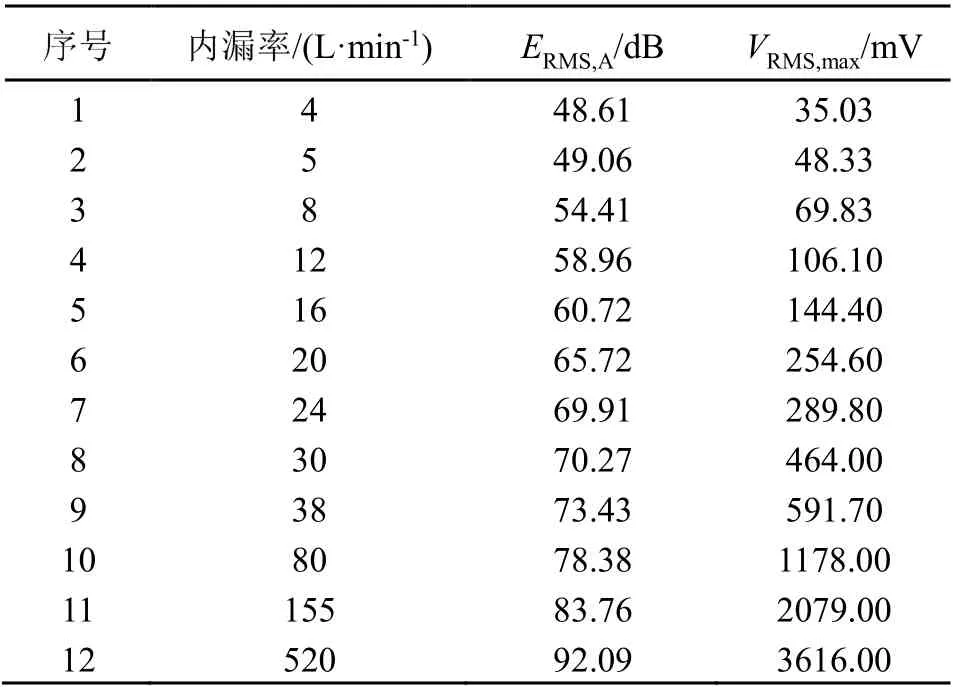
表4 实验数据小波包分解后重构信号的ERMS,A及VRMS值Table 4 ERMS,A and VRMS of the restructured signal after wavelet packet decomposition of experimental data

按照式(4)、(5)拟合的曲线如图4 所示。
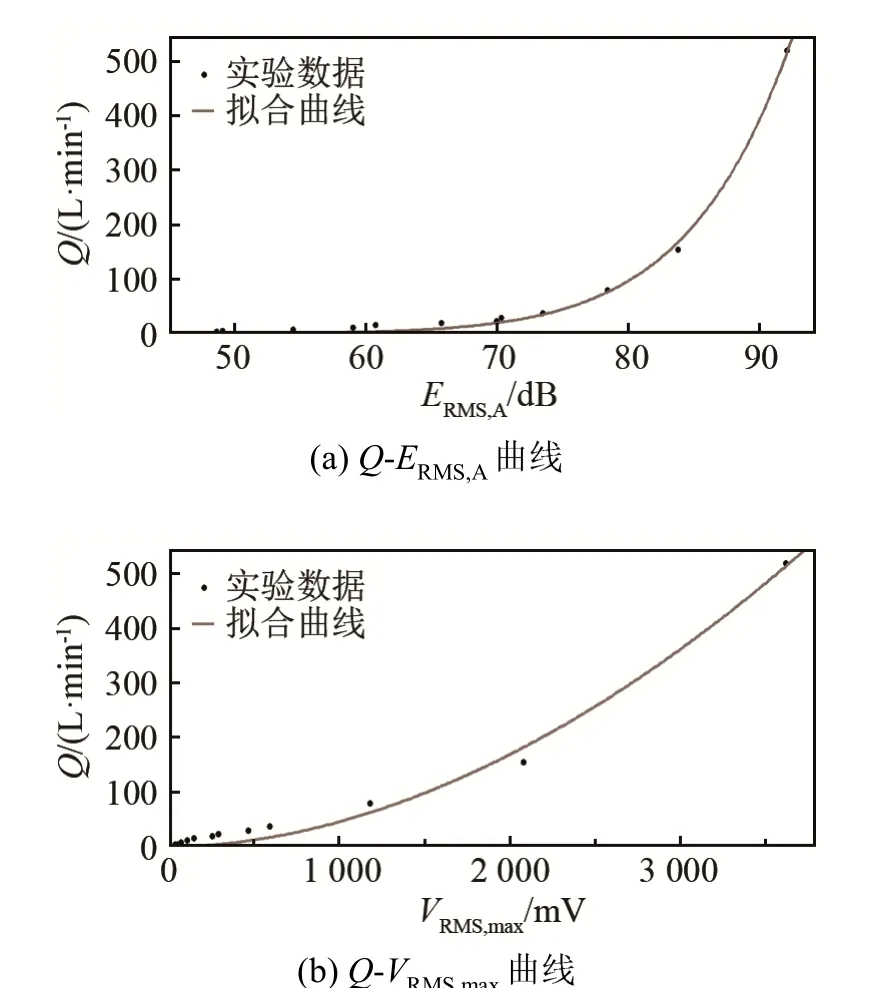
图4 DN50 球阀的Q-ERMS,A和Q-VRMS,max 拟合曲线Fig.4 Fitting curves of Q-ERMS,A and Q-VRMS,max of ball valve
根据式(4)、(5),对6#、10#、12#实验ERMS,A数值对应泄漏流量进行估算并计算估算误差,结果如表5 所示。

表5 内漏率及其相关参数的估算Table 5 Estimates of internal leakage flow Q and the relevant parameters ERMS,A and VRMS,max
VRMS,max在小泄漏流量范围估算误差达到了24%;ERMS,A估算误差最大为9.82%,最小值为4.45%,估算精度符合工程应用要求。
4 结 论
本文针对工程阀门泄漏检测需求,对多种阀门类型、阀门尺寸在不同压力下进行了实验研究,基于理论分析和实验研究得到如下主要结论:
(1) 构造新的阀门内漏声发射评价参量ERMS,A,并通过模拟内漏实验将ERMS,A-Q 曲线与VRMS-Q 曲线比较,结果表明ERMS,A与VRMS曲线变化趋势相同,且ERMS,A曲线估算误差更小,即ERMS,A在阀门内漏评价方面具有更高估算精度;
(2) 相同实验压力下,ERMS,A与内漏率分别取对数后二者呈线性函数关系;相同内漏率下,实验压力越高,ERMS,A值越大;
(3) 傅里叶分析结果表明,对于相同阀门,在不同压力下泄漏信号峰值频率的分布范围相同,处于同一小波包分解频带内;
(4) 在微小泄漏、小泄漏、中等泄漏三个泄漏等级下,采用ERMS,A对泄漏量的估算误差低于10%,表明ERMS,A参量能准确应用于现场阀门的内漏监测评价。
