基于掌握学习理论下的微课辅助教学实践*

广东省广州市聚德中学()

平时的数学教学中，数学老师总有这样的苦恼，题目讲过了好多次了，学生怎么还会错呢? 虽然知道多讲几次会提高答对率，但是，教学进度紧、教学时间往往不允许.学生总会有这样的烦恼：明明上课听懂了，再次遇见类似的题目，怎么还是做不出呢? 针对这两点，笔者用一道特殊四边形背景下的将军饮马问题，在一个班级进行测试，试图回答3个问题：(1)学生要讲几次才能达到90%的准确率? (2) 微课要如何嵌入更有效? (3)将军饮马问题的最大难点是什么?

1 测试班级学情

测试班级的总体情况：八年级，人数：47.学生总体情况：八年级上册期末测试，该班平均分在海珠区排名第5.

2 测试过程

2.1 初次遇见，11人给出正确答案

如图1所示，正方形ABCD的面积为12，ΔABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为( )

图1

本道题是八年级下学期学完平行四边形，某份复习卷的第10题(选择题最后一道)该题考察的是正方形背景下的将军饮马问题：线段之和的最小值.学生要在较多线干扰的情况下识别将军饮马问题，要找到点P，能由正方形面积求出边长.关键点：知道为什么点P是BE与AC的交点，BE的长度就是所求的PD+PE最小值.

2.2 同学交流，换个背景

小测题目：如图2，菱形OBCD，B(5,0),M(0,1)，K是OC上一点，求DK+MK的最小值.

图2

这次测试是在第二天，上述题目没评讲，只是学生之间有交流过，19个学生结果对，其中，14个学生的图没画完整，无法判断是否真会.该题与试卷上的题目不同的是：换了一个背景，由原来的正方形到菱形，不过，这道题目的线没有上述题目多.

2.3 听完微课，第3次测试

笔者在平时的教学中，多次尝试用PPT+录屏软件的方式录制微课，这次的微课做了两点改动：由原来教师主讲改为让学生讲，采用录像的方式，再把视频嵌入微课中；在听微课过程中，多了一个步骤：暂停画面，让学生解释微课中最关键的地方.

第一、微课设计的主要流程

(1)将军饮马问题复习(学生讲，图3-1是视频照片).

(2)题目分析(学生讲，图3-2，图3-3是微课画面)

图3-1

图3-2

(3)信息技术加入：几何画板的嵌入(图3-4)，动态演示，小结回顾(教师讲).目的：更加直观易懂，降低难度.

图3-3

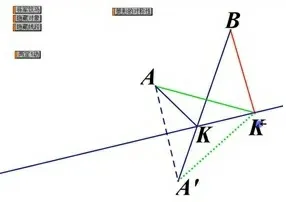
图3-4

(4)突破难点：学生听完微课，解释为什么K 就是满足条件的点.(图3-5和图3-6是学生上讲台解释为什么找到的点符合要求)

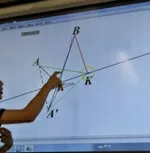
图3-5

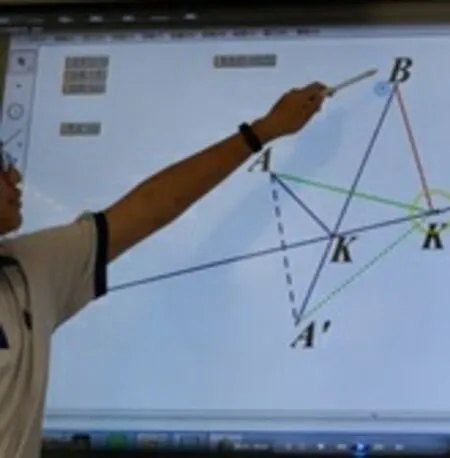
图3-6

第二、检测题目：如图4，已知正方形ABCD边长为4，E是AD的中点，K是BD上一动点，求KE+AK的最小值(要求先在图5中找到点K)

图4

图5

这次题目与第2次的小测题目类似，变化之处：由菱形变为正方形，由坐标形式变为已知中点.

第三、测试情况

让第2次没做对的学生重测，28人中有24人做对，答对百分比：85.7%.

2.4 第4次测试

全班46(1人请假未到校)，1人做错.

(1)测试题目

已知图6，正方形ABCD面积为18，ΔCDE是等边三角形，P是BD上一点，则PA+PE的最小值为________.

图6

图6与图1非常接近，改变之处：面积的数字变化，等边三角形由原来以AB为边改为以CD为边.

(2)测试结果

46人小测，结果正确的有45人，正确率：97.8%.45个答案正确的学生中，8个学生画出了点P，8个学生中，有1个学生画的是点E的对称点(刘同学)最快速度上交的两个同学没画图，直接写答案(陈与黎)；唯一做错的那个学生前几次测试都没答对.

(3)典型答卷及学生访谈情况

采访4个学生：黎同学，图上没画出P(图7-1)；钱同学，P是对角线交点(图7-2)；刘同学：找E的对称点(图7-3)；欧同学，做的最慢.

答题情况及师生对话如下：

师：为什么没看到你找点P，答案也做对了呢?

黎：面积是18，求边长，结果就是边长.

师：你怎么知道的呢?

黎：有规律啊！试卷上那道题的答案就是等于边长.

图7-1

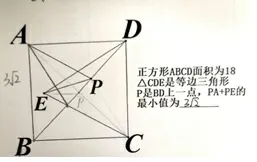
图7-2

师：你找的P是对角线的交点，为什么结果对了呢?

钱：我也不知道.

师：上周你的答案是对的.

钱：碰巧的.上次好像会了，但图形一变化，我又不会了.

图7-3

师：你做的是点E的对称点，怎么求PA+PE呢?

刘：不知道.

师：可是，你的答案做对了.

她不好意思地笑了.

采访欧同学，该同学在第4次测试时，迟迟找不到P，最慢速度上交的学生.

师：是哪个步骤没想到呢?

欧：我当时找的是E的对称点，没找C的对称点.

3 测试情况小结

3.1 题目有区分度

47个学生中，有11个学生第一次做对该题，排除个别学生猜对答案的情况，该班能做对的学生对将军饮马问题认识较为深刻.这11个答对的学生中，陈同学和谭同学是之前帮忙录制微课的学生，在指导他们如何讲时，花了大约1个小时来研究如何讲这种类型的题目(微课流程的第2个画面).

3.2 微课使用合理

微课8分钟左右，针对动点问题，使用了较为直观的几何画板软件，在解题可视化方面，发挥了一定的作用；加上两个学生的解释，在化解难点方面起了一定的作用，28人测试，有24人能在改变图形后做对，答对率85.7%，相对于学生自由交流的准确率40%，准确率有了较大的提升.

4 结语

美国著名心理学家和教育学家布卢姆提出掌握学习理论：只要给予足够的时间和适当的教学，几乎所有的学生都能完成对教学内容的掌握，在该理论下，不存在差生或优等生，它将教学指向班级中大多数学生.而面对学生学习能力，学习风格等的差异所导致的所需学习时间，学习地点等个性化的学习需求问题，就需要个性化的学习资源的支撑，需要教师个性化的辅导答疑.

这个测试表明：学习是需要反复的，一道数学题由原来大约四分之一学生会做，到几乎全班会做的过程中，经历了学生之间交流，微课辅助等不同形式.

在微课加入的过程中，除了学生要认真听，还得有针对性地讲出微课中的难点，例如将军饮马问题不仅仅是要识别这种模型，在当时讲这个内容时应该着重要学生感受为什么这种方法找到的点就能使线段和有最小值.

第4次测试的正确率看起来蛮理想，但真正懂的学生有多少，还需从画图，访谈等方式，才能确切知道学生是否真会，因为学生做对题目，可能像黎同学所说：因为她找到了规律，这种情况只能适用于遇见的题目与之前的题目很相似.

教师在讲解题目，特别是微课录制时，最好能把题目关键点分解，最后把解题过程步骤化，让学生在解题过程中清楚自己在哪个环节有难度.设计微课要针对细，小，容易忽略的容易混淆的知识点设计，深入细化，登记好微课后记，建立微课的学习情况，反馈，使用心得等资源.只有重视细节，微课的辅助、反复功能才能收到有较好的效果.