问题情境下的初中数学探究式教学分析

李建峰

摘 要：文章对初中数学问题情境教学的优势进行了介绍，并阐述了探究式、生活式、矛盾式问题情境的创设方法。最后以几何教学为例，通过案例分析的方式探究“平行四边形性质”的应用方法。力求通过本文研究，使学生的数学兴趣得到激发，逻辑思维与创造力得到全面提升，實现智力与思维的综合发育。

关键词：问题情境;初中数学;探究教学;几何教学

中图分类号：G633.6 文献标识码：A 收稿日期：2020-07-10 文章编号：1674-120X（2020）34-0054-02

在新课标背景下，初中数学课堂发生较大改变，师生角色开始互换，学生的主体地位得到了充分肯定，在课堂上便能体验情境，可见问题情境的创建为数学教学模式改革提供了新的思路。这就要求教师带领学生在各类问题情境中探究和学习，使学生的兴趣与逻辑思维得到提升，充分体验数学知识与生活间的联系，并在生活中灵活地运用。

一、初中数学问题情境探究教学的优势

（一）点燃学习热情

数学学科蕴含着大量知识与符号，且大多具有抽象性特点，对初中生来说较为枯燥，需要学生充分地发挥逻辑思维探寻数学规律，否则学习难度将会提升。因此，教师点燃学生学习欲望与热情显得十分重要。在课堂教学中，教师可通过创设问题情境的方式，给抽象的知识与符号赋予生活意义，以此降低学习的难度，促进学生消化理解知识点，使其对数学产生兴趣。学生还可以将旧知识与生活经验结合，针对实际问题进行探究思考，最终独立解决问题，体验成功的快感。此种教学模式与学生认知特点相符，有助于知识体系的构建与完善，对培养学生数学兴趣与动力具有重要意义。

（二）培养问题意识

数学学习需要经历大量的思维活动，多数时间里课堂氛围较为沉闷，教师对学生严格要求，未给予充足的思考与探究时间。在传统课堂中，大多由教师来讲解传授知识，然后马上开展习题训练进行知识巩固，这一过程中，课堂气氛十分紧张，学生处于被动接受的状态，对教师产生了较大依赖，不利于问题意识与质疑能力的培养。教师通过创设学习情境，引入多媒体等辅助教学设备，可有效刺激学生的感官，通过图文并茂的方式培养学生思维，引导其独立思考，使其带着问题进行学习，在情境中细心探索，在发现问题后能够多角度思考并解决，以此提高问题意识与解决问题的能力。

（三）开拓逻辑思维

在现代化数学教学中，教师应重视情境教学模式的构建，以此培养学生的逻辑思维与核心素养。例如，教师在讲解“几何图形”这一章节时，可给出一道相关应用题，鼓励学生根据自己对题目的理解画出这一图形，并在探究后解答问题。在学生不断的尝试与思考中，教师应引导和启发，保障其思路不偏离正确的方向，从而又快又准地解答问题。在此模式下，不但学生的逻辑思维得到训练，还可拓展学习范围。再如，计算立体图形面积时，教师可通过创设探究情境，鼓励学生探索计算，最终得出正确答案，提高数学成绩。

二、初中数学问题情境教学模式的生成措施

（一）营造生活式问题情境

数学知识来源于生活，又服务着人类生活，这也是该学科的魅力所在。问题情境不但是教师的教学重点，也是学生探究学习中的薄弱之处，一些学生在面对数学问题时常产生畏惧心理，不愿意探究。教育心理学专家指出，通过发挥数学生活应用特性，可以激发学生对问题的探索与求知欲望，进而提高学生的学习情感，增强能动意识。例如，教师在讲解“中心对称图形”时，可引入生活中具有中心对称的物品，如扑克牌是人们休闲娱乐的主要道具之一，将几张扑克牌旋转后可呈现怎样的效果，是否会发生变化？学生在此种教学情境的影响下，对所学知识产生较强的亲近之感，探究欲望被充分激发，为问题解答奠定了浓厚的情感基础。

（二）创建矛盾式问题情境

问题学习的目标在于使探究者能够知其所以然，更好地把握整体，增加知识的深度与广度。在数学教学中，教师可通过设置矛盾性问题情境，激发学生的探究欲望，利用学生主体认知冲突与心理疑惑，使其带着问题投入数学案例探究之中。例如，教师在讲解“平行线判定”一课时，为了调动学生的探究欲望，在探究假设相同平面中有两条直线均垂直于某一直线，则这两条直线是否平行？请说明理由？时，学生在证明完毕后，教师可针对学生的解析情况进行补充，并提出在这一案例中，为何一定要有在相同平面内这一限制条件？不要这一条件是否可行？此时，学生心里便会产生疑惑，形成认知矛盾，探究与讨论的欲望被激发，使这一问题得到深入探究。

（三）构建探究式问题情境

在以往单一化教学模式下，学生的学习兴趣会降低，甚至在课堂上昏昏欲睡。对此，教师可构建探究式情境，精心设计问题，吸引学生注意力，锻炼其实践能力，使学生在亲身操作中体会数学的奥秘，促使静态知识动态化。例如，教师在讲解“四条边相同的四边形、对边相同的四边形时”，可事先制作一些道具，使学生在亲眼看到、亲手触摸中证明，解析考量后论述，锻炼其动手学习能力，还可激发学生的创造能力;再如，将此种教学方法应用到“平移”教学中，学生通过亲自动手移动，形象具体地感受线段、平面之间的变化，更有助于知识记忆与理解。该方式在几何教学中应用的效果十分显著。学生在教师的引导下亲自动手并解决问题，体验数学的乐趣与奥秘，使学生的学习动力得到显著增强。

三、初中数学问题情境探究教学的案例分析

（一）教学设计

在以往的课堂教学中，学生对几何知识兴趣不高，问题意识缺失。为改善这一现状，笔者引入“问题情境”教改实验，以“平行四边形性质”教学为例，在教材中设置这一例题。

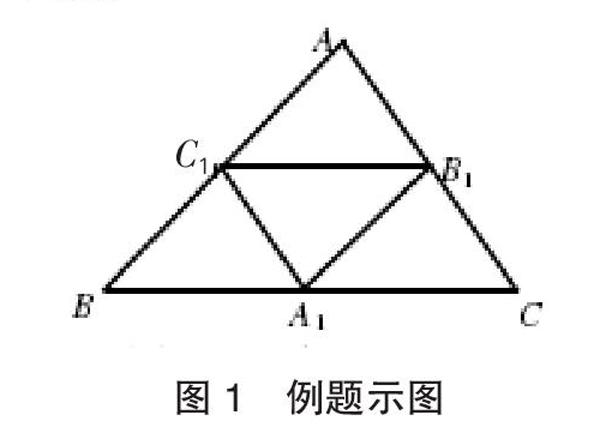
例题：已知图1中A1B1与AB平行，B1C1与BC平行，A1C1与AC平行，求证：∠C1A1B1与∠A相等、∠A1B1C1与∠B相等、∠B1C1A1与∠C相等，且A1、B1、C1分别为△ABC各边的中点。

对此，可通过创设情境引出“平行四边形性质”等常规问题，还应引导学生提出具有探究性的非常规问题，拓展学习的深度与广度。为达到这一目标，教师可做以下教学设计：首先，省略該题中的求证部分，保留已知图形，将其作为情境1，引导学生提出包含教材中两个结论的常规性问题。然后，强化已知条件，将△ABC变成等腰三角形作为情境2，引导学生提出“图形中正方形、长方形的形成条件为何？”等问题，这时问题便会反作用于情境，激发学生的探究热情。最后，尽量引导学生观察接触“极限”问题，并在特定情境下根据所提问题开展探究活动，将知识扎实掌握和内化。

（二）教学过程

教师利用多媒体大屏幕出示情境1，题目如下：

例题：已知图1中A1B1与AB平行，B1C1与BC平行，A1C1与AC平行，求证的内容如下：

（1）四边形AC1A1B1、CB1C1A1与BA1B1C1为平行四边形;

（2）三角形AB1C1、BA1C1、A1B1C与A1B1C1均为全等三角形;

（3）线段AB、BC与AC的长度分别为2倍的A1B1、B1C1与A1C1;

（4）A1、B1、C1分别为△ABC各边的中点。

学生1：“△A1B1C1是等腰三角形吗？”

学生2：“不是，除非已知该图形为等腰三角形。”

教师借机引导：“如果△ABC为等腰三角形呢？”并由此出示情境2，图1中△ABC为等腰三角形。

学生3：“如果它是等腰三角形，则图中三角形都等腰。”

学生4：“此时四边形AC1A1B1的四条边长度相等。”

教师及时肯定：“这种四边都相等的图形便是菱形。”

学生5：“那剩余的两个四边形，CB1C1A1与BC1B1A1是否同样为菱形？”通过师生通过探究讨论可知，这两个四边形的四边长度不相同，并非菱形。

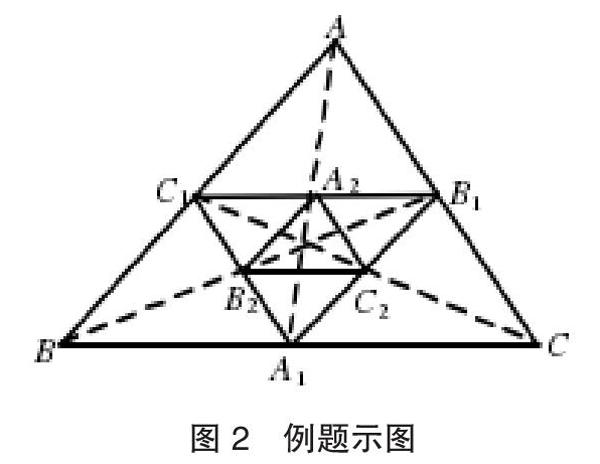
教师追问：“如何将它们变成菱形？”同时，引导学生观察并思考：“根据前面求证出的结论可知，如果△A1B1C1为△ABC三边的中点……”学生马上得出△A1B1C1各边的中点。教师询问缘由，学生答“因为平行四边形的对角线相互平分”，这时便得出第二个三角形，如图2所示。

此时，教师询问学生是否有新的发现。学生起立回答：“一直这样做下去，最后的三角形是否会变成一个点？”这时，教师询问缘由，大家纷纷沉默。教师提醒学生结合前面得出的三角形面积关系，然后师生一同对以下问题进行探究：

假设S△ABC为S1，S△A1B1C1为S2，令S1为1，则S2=S1/4=1/4，S3=S2/4=1/4²，…，根据这一规律，学生最终找出了数学规律，即：Sn=1/4^n-1。

（三）教学效果

在本节课中，教师将一个看似简单的例题进行转变后，根据所提问题创设情境，在教师的启发与引导下，学生思维层层深入，由表及里地提出常规性、发展性与探究性问题，从而牢牢掌握平行四边形性质，完成教学内容;还打破了课本局限性，使所学知识得以延伸，培养了由一般到特殊的数学思维，使自身的学习主体性与探究能力得到全面提升。

综上所述，在初中数学教学中，问题情境的创设有助于吸引学生注意力，激发学生对数学问题的探究与求知欲望，从而全身心地投入数学解题之中。作为教师，应积极转变教学思维与方法，结合课本知识创设探究式、矛盾式、生活式的问题情境，在传授理论知识的同时培养学生的实践能力，促进其数学素养与综合能力的全面提升。

参考文献：

[1]吴世昌.基于问题学习的初中数学情境教学模式探究[J].教育科学·全文版，2019（3）：256.

[2]陈泓羽.基于问题学习的初中数学情境教学模式探究[J].数学学习与研究，2019，13（14）：28.