D-S证据融合的坦克火控系统混合故障诊断

李英顺，江山青,2，陈悦峰，周建军，张银图,2

(1.北京石油化工学院 信息工程学院，北京 102600；2.北京化工大学 信息科学与技术学院，北京 100020；3.北京特种车辆研究所，北京 100071)

坦克是我国陆地作战的主要装备，其庞大的体型、超大的质量、复杂精密的结构都给坦克的故障诊断带来了诸多不便。而且随着坦克作战性能的提升，设备复杂度进一步提高，其维修难度也进一步加大。现如今对坦克的维修主要还是依靠有经验的专家，但是专家的数量非常有限，专家的时间和精力也非常有限，因此坦克故障诊断的智能化已亟不可待[1]。

专家系统就是将多位专家具有的经验、知识融合在一起，模拟人类专家的思维方式，得到跟专家类似的推理结果。这非常符合坦克的实际情况，因此很多学者都已经开始把专家系统应用到坦克故障诊断中来。

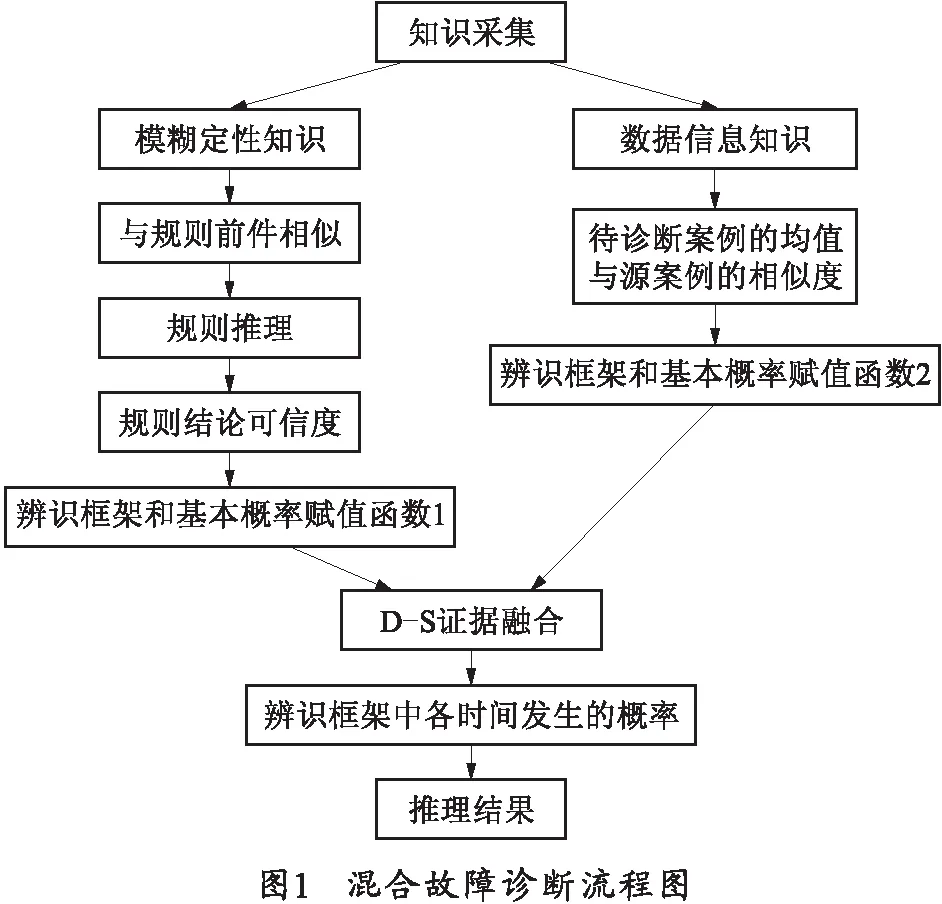
目前专家系统主要有基于案例的[2]、基于规则的[3]、基于模型的、基于边框的，其中基于案例和基于规则的专家系统应用的最多、最广泛，效果也较好。大多数专家系统目前都只是使用其中一种方法，使用单一的方法可能使某些有用信息遗漏掉，这样出现误诊漏诊的概率较大。笔者根据诊断信息和专家经验知识，分别使用基于案例和基于规则的方法得到两个推理结果，然后使用D-S证据理论[4]把两种方法所得的结果进行融合，组成了混合专家系统。混合专家系统使所有的故障信息均得到充分利用，提高了信息的使用效率，进而提高了故障诊断准确率，降低了误诊漏诊率。

1 基于案例的推理方法

案例推理是一种相似或类比的推理方法，通过用当前的状态和事实类比知识库中过去同类问题的解而求解当前问题，即利用以前的经验和事例来解决现在的问题。完整的案例推理包含匹配、复用、修正、学习等过程[5]。目前案例知识的表示方法有多种形式，如语义表示法、框架表示法、形式概念表示法等等。基于案例的推理方法直接利用以往解决问题的实例，能有效地解决知识表达困难或无法表达的领域问题。

1.1 案例的知识表示

这里采用矩阵的形式保存案例库中的源案例，然后通过数据相似度进行匹配，最后得到推理结果。采用矩阵的形式表示源案例，案例表示结构清晰，易于建立案例库，且各个源案例之间没有耦合联系，可以很方便地根据实际情况对案例库中的知识进行修改、调整，也可以很方便地添加新的案例而不影响之前的案例知识结构。案例知识库矩阵如表1所示。

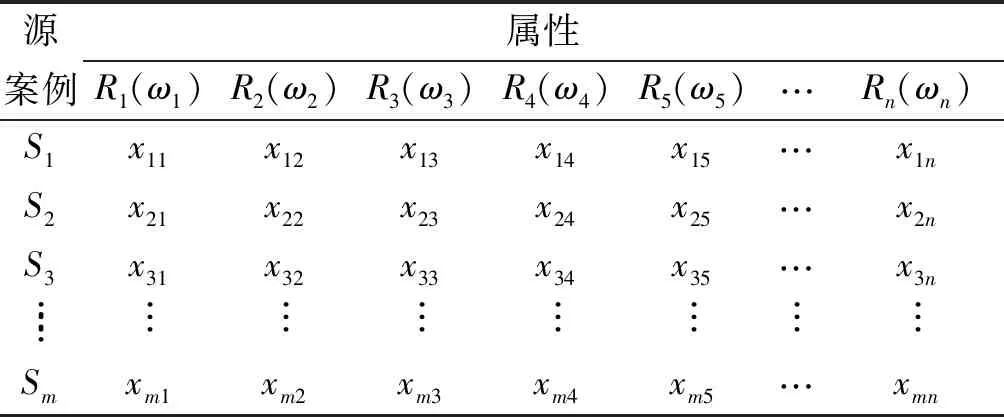
表1 案例知识库矩阵

表1中Si(i=1,2,3,…,m)为第Si个源案例，m为源案例总数；Rj(j=1,2,3,…n)为第Rj个属性特征；ωj(j=1,2,3,…,n)表示第Rj个属性特征的权重，用于计算待检测案例与源案例的相似度，它也保存在案例知识库中。

1.2 案例相似度计算

在获得待诊断案例x=(x1,x2,…,xn)后，通过计算x与案例库中每一个源案例的相似度，并比较其大小来决定案例推理结果。

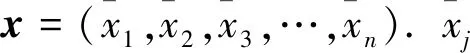
(1)

式中，α、β分别为xj历史检测到的最大值和最小值。

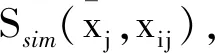
(2)

由式(1)和式(2)可以计算待诊断案例与每一个源案例的相似度，把Ssim(x,Si)(i=1,2,…,m)由大到小排列，取出前5项源案例对应的诊断结果放入到集合Θ1中，Θ1={A1,A2,A3,A4,A5,P},P代表未知故障原因。

2 基于规则的推理方法

基于规则[6]的故障诊断方法是根据专家给出的模糊定性经验知识，通过粗糙集、故障树等理论将其约简、总结、归纳成一条条的规则。大多数基于规则的故障诊断专家系统都是用事实匹配规则的前件，如果事实与某条规则的前件吻合，则得出规则的结论，如果与所有的规则前件都不吻合，则诊断失败。这样不但很难知道所得结果的可靠性，而且对规则的匹配很严格，如果所得事实与所有规则前件都不吻合，但是与某条规则前件很相似，也不会激发该规则，同样会诊断失败。这样就导致了对信息利用不充分，诊断效率低下。针对这种情况，一般有两种解决办法：

1)增加规则数量，把尽可能多的情况考虑进去。这种方法虽然在一定程度上可以提高事实与规则前件的匹配度，但是会给技术人员增加大量的工作，无法把所有情况考虑进去，增加了时间和空间复杂度，最终还是得不到结果的可靠性，难以从根本上解决问题，效果非常有限。

2)在制定规则时，先赋予每条规则一个可信度，然后在进行规则匹配时，先求取每条规则前件与事实的相似度，如果相似度大于阈值α，则可激发该规则，得到规则结论。规则结论的可靠性则可以由规则可信度与规则前件与事实的相似度计算得到。笔者采用的就是这种方法。

产生式规则表示的这种因果关系与人们的逻辑思维方式非常相似，可以很方便地把专家们给出的经验知识表示成一条条规则。再加上可信度因子，可以很好地表示专家模糊经验知识的不确定性。带有可信度因子的产生式规则的表示形式如下：

IFATHENBre(A/B)，

其中：A表示规则的前件，可以是多个事实条件的组合；B表示规则的结论；re(A/B)是可信度因子，表示规则前件A发生概率为1时，得到规则结论B的可信度。

为了便于计算事实与规则前件的相似度，在制定规则时，只保留了多个事实条件“与”的情况。如:

IFa1anda2anda3THENb10.85，

表示当事实a1、a2、a3均满足时，结论b1发生的概率为0.85.

对于规则前件中的事实条件存在“或”关系的，将其拆分为多个规则。如：

IFa1anda2ora3THENb10.8,

则可以拆分表示为两条规则：

IFa1anda2THENb10.8,

IFa3THENb10.8.

把采集的数据放入证据集A中,A={ai|i=1,2,3,…,n},把单个指标ai偏离正常值的范围定义为Ddisa(ai)，它表示了单个指标ai的不可靠度。坦克火控系统大部分的检测信号都是电压信号，其中又分为固定值和范围值。

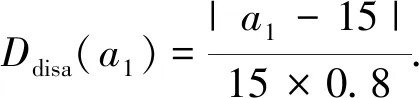
对于范围值，当检测值高于正常范围最大值的0.5倍或低于最小值的0.5倍则属于完全不正常。例如：水平向角速度信号正常范围为-5～+5V，检测值为a2，当|a2|≥7.5 V时，属于完全不正常，Ddisa(a2)=1，当5 V<|a2|<7.5 V时，Ddisa(a2)=

把规则前件与事实证据的相似度定义为Xsim(ri)，有了单个指标的不可靠度Ddisa(ai)，则可以计算产生式规则中整个前件与事实证据的相似度。如果规则前件只有一个事实条件，那么直接以不可靠度Ddisa(ai)作为与该规则前件的相似度，即Xsim(ri)=Ddisa(ai).如果规则前件存在多个事实条件，则可以通过下式计算其相似度：

(3)

式中：Ddisa(ai)表示规则前件中对应的事实证据的不可靠度；n表示事实条件的个数。

当相似度Xsim(ri)低于某个阈值ω，则视为低概率事件，不再进行后续计算。ω的具体取值取决于经验总结，具有一定的主观性。当Xsim(ri)高于阈值ω，则可通过相似度Xsim(ri)与规则可信度因子re(A/B)计算得到规则结论的可信度:

Ci=Xsim(ri)×re(A/B).

(4)

把所得结果按可信度Ci从大到小排列，取其前5项对应的规则结论放入集合Θ2中,Θ2=(B1,B2,B3,B4,B5,P)，其中P同样表示未知故障原因。

3 D-S证据理论融合

D-S证据理论是由Dempster在1967年提出，于1976年由他的学生Shafer进一步发展完善，所以又称为D-S证据理论。D-S证据理论[7]目前已成为处理不确定性信息和融合多种推理结果的重要工具之一，它能综合考虑多源信息中各信息的权重，减少多源信息推理产生的结论分歧。在故障诊断专家系统中，大多数学者都是在单一故障诊断专家系统中应用D-S证据理论融合多个传感器的结果，很少有人把多个专家系统的诊断结果通过D-S证据理论进行融合。

辨识框架[8]和基本概率赋值函数[9]是D-S证据理论中的两个重要概念。辨识框架是指人们对某一问题所能认识到的所有可能的集合，集合中的事件都是独立互斥的，用字母Θ表示。

Θ={A1,A2,A3,…,AN}.

Θ的所有子集组成的集合叫做Θ的幂集，用2Θ表示。

基本概率赋值函数用m表示，定义为：

(5)

式中：φ表示空集；A∈2Θ是幂集中的任一组成元素；m(A)表示证据支持事件A的概率。式(5)表示基本概率赋值函数m对空集不产生信任度，对所有可能发生事件的信任度之和等于1.

对于辨识框架Θ，若m(A)>0，则把A叫做证据的焦元。假设辨识框架Θ下有两个证据对应的基本概率赋值函数为m1和m2，焦元分别为Ai和Bj,则D-S组合规则为：

(6)

式中，k为冲突系数，可以衡量不同来源证据之间的冲突程度，表示为

(7)

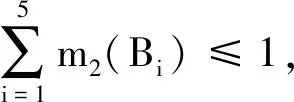
把基于案例的的推理结果Θ1={A1,A2,A3,A4,A5,P}与基于规则的推理结果Θ2={B1,B2,B3,B4,B5,P}的并集作为D-S证据融合的辨识框架Θ，即Θ=Θ1∪Θ2，其对应的m′1，m′2，m′(P)作为基本概率赋值函数。

把融合后的结果按概率大小依次排列，概率最大的为首要可能故障原因。P为未知故障原因，如果最终的推理结果得到P的概率最大，则表明事实与案例库中所有源案例和规则库中所考虑到的情况都不相符，故诊断失败。如果经实际排查找到了故障原因，则可以把该事例放入规则库和案例库，以充实系统的知识库，提高该系统以后的诊断准确率。

基于案例和规则D-S证据融合的混合推理流程如图1所示。

4 实例分析

坦克火控系统是以火控计算机为核心的一套半自动武器系统，其能够实现对“自动跟踪线”、“瞄准线”和“火炮轴线”的单独控制。该系统为炮长提供对战信息，根据目标姿态、距离、环境参数、车辆姿态、弹种、人工装定量和综合修正量等信息，控制火炮实现最高可能精度的射击。

坦克火控系统主要包括观瞄分系统、火控计算机与传感分系统和炮控分系统等部件，根据专家经验和操作人员的总结性知识，总结出故障诊断规则。以炮控箱为例，列举其部分规则：

IF 电源信号故障 and 交流供电异常 THEN 变流机故障 0.80;

IF 电源信号故障 and 交流供电异常 THEN 交流电源线路故障 0.20;

IF 电源信号故障 and 135 V电源异常 THEN T2变压器损坏 0.85;

IF 电源信号故障 and +15 V电源异常 THEN T1变压器损坏 0.70;

IF 水平信号异常 and 水平瞄准控制信号始端异常 THEN 操纵台水平电位器损坏 0.85;

IF 水平信号异常 and 水平瞄准控制信号末端异常 THEN 4号板K7损坏 0.5;

IF 水平信号异常 and 来自陀螺仪组水平角速度信号异常 THEN 陀螺仪组内水平放大器板损坏 0.8;

IF 水平信号异常 and 来自陀螺仪组水平角速度信号异常 THEN 陀螺仪组与炮控箱连线断开 0.1;

IF 垂直信号故障 and 垂直功率输出异常and 检测XS8-9/10故障 THEN 9号板损坏 0.9;

IF 垂直信号故障 and 垂直放大输出异常 THEN SFC放大器板坏 0.75.

通过100组已知故障原因的故障数据，验证基于规则的故障诊断、基于案例的故障诊断和D-S证据理论混合故障诊断的有效性。依次根据不同的方法试验每一组故障数据，最终的统计结果如表2所示。

表2 各方法诊断结果对比 单位:%

从试验结果可以看出：基于案例的知识推理，漏诊率较大，误诊率较小，漏诊率大的主要原因是案例知识库中的案例不够多，知识不够丰富，需要在使用的过程中根据实际情况不断丰富案例库，提高诊断准确率。基于规则的推理虽然漏诊率较小，但是误诊率较大，主要是因为规则可信度因子re(A/B)的主观性太强，难免出现偏差。D-S证据融合的方法很好地融合了两种方法的有效信息，提高了诊断结果的准确率。

5 结束语

以某型坦克火控系统为对象，提出了基于案例和规则融合的混合故障诊断专家系统，首先根据专家经验和历史数据以矩阵的形式建立了案例库，然后用带有可信度因子的不确定性产生式规则表示基于规则部分的知识。根据两种推理方法得到的结果，确定了它们进行D-S证据理论融合的辨识框架和基本概率赋值函数，最后用D-S组合规则把两种推理结果融合得到最终结果。经实际检验，该方法克服了单一方法对信息利用不充分的缺陷，提高了故障诊断准确率，减少了漏诊误诊率。