考虑非线性摩擦的电动伺服缸加载系统鲁棒自适应控制

李 辉，杨 绿，吴怀超

( 贵州大学 机械工程学院，贵州 贵阳 550025)

相较于砝码和液压伺服加载，电动伺服缸可动态加载，具有传动机构简单、系统稳定高效以及加载精度高等特点，越来越多地应用于高精度动态加载系统中，但其伸缩活塞与缸体的非线性摩擦特性、外部干扰和参数不确定性对电动伺服缸加载精度和动态响应特性影响较大。因此，电动伺服缸控制器设计中，有必要纳入上述非线性摩擦特性和参数不确定性因素以保证加载精度、跟随效果和稳定性。

近年来，随着动态加载精度的要求越来越高，电动伺服缸控制器设计引起了不少研究者的关注。如，秦幸妮等[1]将自抗扰技术应用到电动伺服缸中，设计了系统位置环的自抗扰控制器。结果表明，自抗扰控制器控制的电动伺服缸定位精度高。此外，为满足电动缸位移与力的伺服控制需求，张爱龙等[2]提出了带前馈的PD闭环控制器，该控制方法具有较好的力和位移跟踪效果。针对伺服系统中存在的非线性扰动问题，龙力军[3]提出了一种自适应控制器，该控制器解决了系统未知扰动参数估计问题，但未考虑系统非线性摩擦问题。为了进一步补偿电动伺服缸非线性摩擦问题，山显雷等[4]基于LuGre摩擦模型和PD控制算法，设计了摩擦补偿控制器，提高了位置跟踪精度，但该研究未考虑外部扰动和系统参数不确定性问题。

针对上述问题，本文设计了系统的自适应律，实现系统未知参数的在线估计，并借助自适应控制器对外部总体干扰进行补偿。通过仿真验证所提鲁棒自适应控制器的加载力跟踪精度和动态响应特性。

1 电动伺服缸加载系统动力学模型

电动伺服缸加载系统结构如图1所示，其传动系统由伺服电机、减速带、轴承、滚珠丝杠、弹簧等元件组成。

图1 电动伺服缸简图Fig.1 The electric servo cylinder schematic

电动伺服缸通过电机驱动带动减速机构中的同步带，再通过联轴器带动滚珠丝杠螺母副，最终带动活塞缸完成加载。通过对电动伺服缸加载系统分析，得动力学模型为[5]

(1)

式中：J为丝杠转动惯量，kg·m2；φ为丝杠转角，rad/s；fL为导轨粘性系数，N·m/(rad·s-1)；F为非线性摩擦力矩，N·m；u为加载系统总输入转矩，N·m；M为干扰力矩，N·m。其中，非线性摩擦力矩的LuGre模型为[6]

(2)

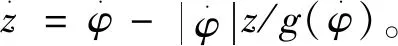
(3)

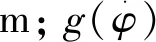
(4)

式中：Fc为库伦摩擦力，Fs为最大静摩擦力，Vs为切换速度，跟踪误差e=φ-φd，φd为期望转角。定义滑膜面函数为[7]

(5)

(6)

由式(5)推出：

(7)

将(7)式两边同乘J后，把(1)、(2)、(3)式代入(7)式得

(8)

ML+u。

(9)

控制目标：设计自适应鲁棒控制器，使得闭环控制系统的跟踪误差快速收敛。假设：总的干扰力矩|ML|≤D，式中D未知。

2 鲁棒自适应设计

整个电动伺服缸加载系统中主要包含了非线性摩擦、参数不确定性和外界扰动等特性，因此采用鲁棒自适应控制器，整个电动伺服缸控制系统的结构框图如图2所示。

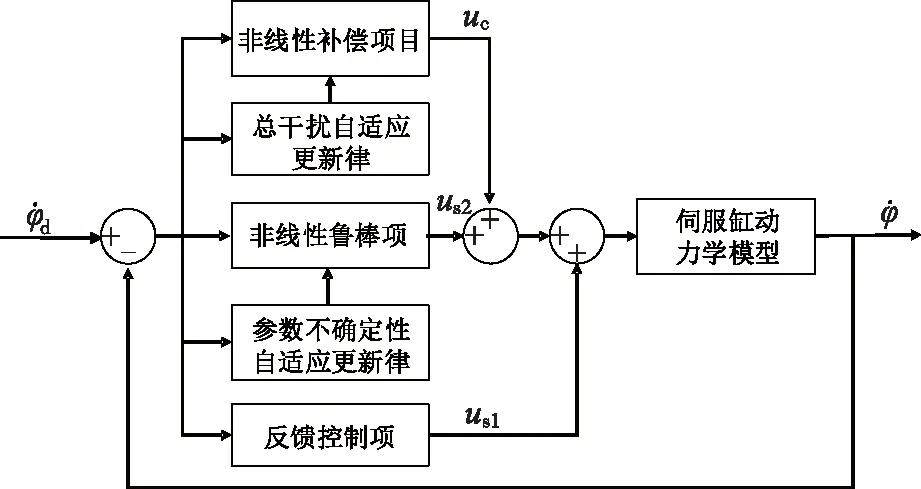
图2 电动伺服缸控制系统结构Fig.2 Electric servo cylinder control system structure

设计鲁棒自适应控制律为[8]

u=uc+us1+us2。

(10)

式中：uc为自适应补偿项，us1为反馈项，us2为鲁棒项，令θ1=J、θ2=FL、θ3=D，则根据各控制项的特性设计得

(11)

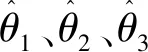
(12)

式中：Γ1、Γ2、Γ3、γ1、γ2、γ3为正系数。

证明1：当系统稳定到达滑膜面时，r=0，取Lyapunov函数[9]：

(13)

代入式(5)得

=-2l+1k2(V0)l+1/2≤0。

(14)

由式(14)中得出V0(0)在t=0时为稳定点，证毕。

证明2：当系统稳定未到达滑膜面时，取正定函数：

(15)

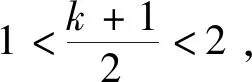
(16)

取η0=max(η1,η2}得

则滑膜面在T时间内收敛于邻域内：

证毕。

3 仿真结果与分析

为了验证所设计的鲁棒自适应控制器的控制效果，依据式(11)、(12)，运用Matlab/Simulink仿真软件搭建了仿真模型；控制器参数设置为k1=10,k2=0.1,k3=30,g=3,h=5,γ1=γ2=γ3=1；电动伺服缸的参数如表1所示。

表1 电动伺服缸参数Tab.1 The electric servo cylinder parameters

输入期望加载力F=3/πsin(t)的正弦信号，仿真时间设置30 s，加载力跟踪仿真结果如图3所示，从图中可以看出，控制系统可在0.4 s内完成跟随。图4是ARC控制加载力跟随误差与传统的PD控制跟踪误差对比图，从图中得出鲁棒自适应控制的稳定性更好、跟踪效果更优。

图5为外加功率为0.001，采样时间为0.1 s的白噪声干扰下的仿真图，从图5可以看出，在外加干扰条件下，ARC控制相比PD控制的加载力跟踪效果更好，误差幅值下降了60%左右。同时，为验证变载荷跟随效果，分别给定不同的加载力：3 N、4 N、6 N，仿真时间为3 s，如图6所示，系统在0.4 s内也可以完成变信号下的快速跟踪。

图3 ARC控制加载力跟踪曲线Fig.3 The ARC control load tracking curve

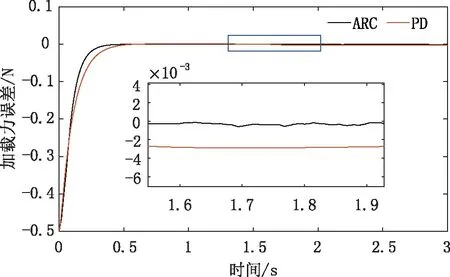
图4 ARC与PD控制加载力位置误差曲线Fig.4 The ARC and PD control position error curve of loading force

图5 外加干扰下ARC与PD控制加载力误差曲线Fig.5 The error curve of loading force controlled by ARC and PD under external interference

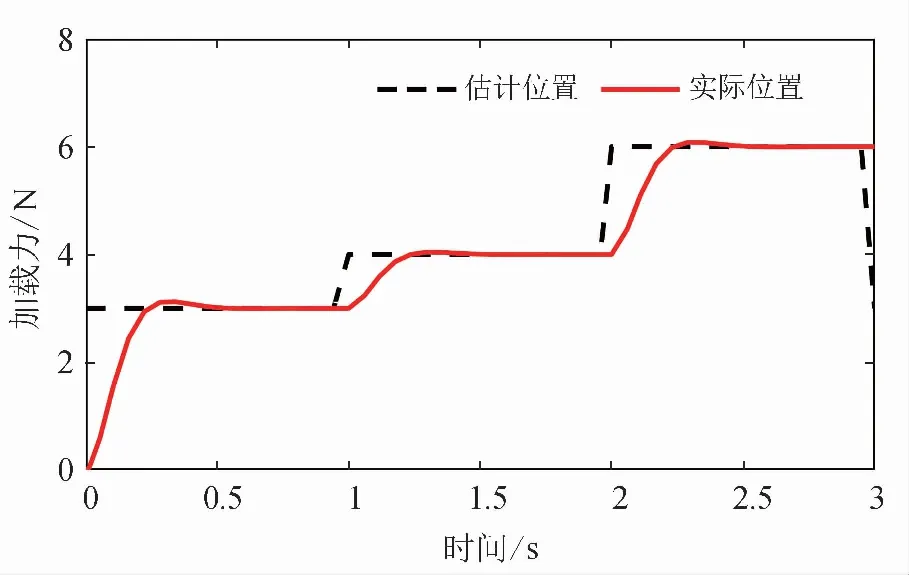
图6 变载荷下ARC控制跟踪曲线Fig.6 The ARC control tracking curve under variable load

4 结论

本文针对电动伺服缸非线性摩擦特性、外部扰动以及参数不确定性对伺服精度和动态特性的影响，设计了一种鲁棒自适应控制器，该控制器通过将非线性摩擦纳入外部扰动进行补偿。经Lyapunov理论证明，所提控制器可以在有限时间内快速收敛到平衡点附近的邻域内；此外，经仿真验证，鲁棒自适应控制能很好地跟随期望加载力，在外部干扰作用下，也能在有限时间内快速收敛到平衡点附近的邻域内；与传统的PD控制器相比，鲁棒自适应控制器的稳定性和加载力跟随效果更优。