单轴循环冲击下花岗岩力学特性与损伤演化机理
2020-03-20王志亮田诺成
王志亮,杨 辉,田诺成
(1.合肥工业大学 土木与水利工程学院,合肥 230009; 2.合肥工业大学 资源与环境工程学院,合肥 230009)
岩石是由矿物或岩屑在地质作用下按一定规律所组合成的集合体.不同的岩石由于其成分、结构与构造不同,在力学特性上呈现出很大的差异性.目前,在一些工程实践中岩体会受到多次冲击荷载的扰动,如地下硐室的钻爆开挖、隧道掌子面的爆破施工以及机械开挖扰动都会给岩体施加循环动载.在循环冲击荷载下岩石内部的微裂隙会不断增多、扩展,进而相互贯通,形成宏观裂纹[1].因此,研究岩石在循环冲击荷载下的动态力学特性对于工程实践具有重要意义.
目前,针对岩石类材料在循环荷载下的动态力学性能问题,许多学者已经开展了相应的研究工作.林大能等[2]利用压力试验机对大理石进行了循环冲击试验,发现相同荷载冲量下围压的存在可以提高试样的冲击强度,并降低其损伤演化的速率;金解放等[3]基于自行研制的SHPB装置,研究了岩石在循环冲击过程中典型的动态应力-应变曲线及反射波和透射波规律,并将应力-应变曲线分为5个阶段;朱晶晶等[4]对花岗岩进行了单轴循环冲击试验,发现花岗岩的力学特性随着冲击次数的增加而逐渐劣化,且岩石的累积比能量吸收值在破坏前缓慢增长,而在破坏瞬间急剧增长;唐礼忠等[5]对矽卡岩进行了轴压和循环冲击荷载共同作用下的试验研究,发现岩石在不同轴压下的应力-应变曲线存在回弹和不回弹两种特性;许金余等[6]研究了循环冲击荷载下围压对斜长角闪岩动态力学特性的影响,指出相同围压下,岩样的能量吸收率随着应变率的提高而增大;宫凤强等[7]研究了砂岩在三维静载和循环冲击荷载共同作用下的动态力学特性,发现围压不变,轴压比在0.52~0.87变化时,砂岩的抗压强度会随着轴压的增大而减小;Wang等[8]研究了不同温度热处理花岗岩在循环冲击下的损伤演化规律,发现200 ℃后岩样对循环冲击荷载的抵抗能力最强,600 ℃后岩样的抵抗能力最差,400~600 ℃存在一个花岗岩的温度阈值;金解放等[9]对Logistic函数进行了逆变换,并建立了岩石在静荷载与循环冲击荷载共同作用下的损伤累积演化模型;Wang等[10]进行了钢纤维混凝土的循环冲击试验,发现添加少量的钢纤维可以显著提高混凝土的抗冲击性能,且相对于普通混凝土其破坏时裂缝尺寸较小.
与静态循环载荷下岩石力学特性的研究成果相比,动态循环荷载作用下岩石的力学特性还处于起始阶段,且其理论研究明显落后于工程实际应用.基于此,本文拟利用改进的SHPB装置,对黑云母花岗岩进行了单轴循环冲击压缩试验,重点探究花岗岩的动态力学特性和损伤演化机理,并发展出岩石在循环冲击荷载下裂纹起裂应力一种近似确定方法,从而尝试对此类岩石在循环冲击试验中表现的现象进行合理的解释.
1 试 验
1.1 试样制备
试验材料取自陕西华山地区的黑云母花岗岩,其主要矿物成分有微斜长石Mc (41%)、斜长石Pl (27%)、石英Qz (22%)与黑云母Bt (7%)等,偏光显微观察如图1(a)所示.为减小离散性和各向异性对岩石力学性质的影响,所有试样均采用水钻法从同一块新鲜完整的大块岩样上沿同一方向钻孔取得.根据国际岩石力学学会(ISRM)的建议[11],将试样加工成φ50×25 mm的圆柱体,加工后的黑云母花岗岩试样如图1(b)所示.试样经打磨后,其端面不平行度控制在0.05 mm以内.

图1 花岗岩组分及试样
1.2 试验原理
目前,岩石动力学测试设备常见的有高压动三轴仪、分离式霍普金森压杆(SHPB)和轻气炮等[12].本次试验采用华北理工大学改进的SHPB装置,如图2所示.该测试系统主要由气腔室、纺锤形冲头、入射杆、透射杆、缓冲杆、数据采集系统和分析系统等组成.弹性杆和冲头由高强度合精钢制成,密度为7 795 kg/m3,波速为5 797 m/s.入射杆与透射杆的长度均为2 m.该装置最显著的特点是冲头为纺锤型,其撞击入射杆后产生的半正弦波形有效增加了入射波的上升沿时且消除了波形的弥散效应,这有利于冲击过程中弹性杆的一维应力传播及试样两端达到应力平衡[13].
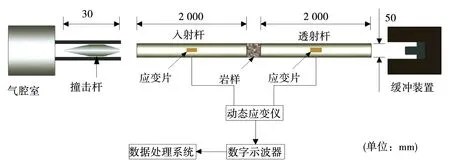
图2 改进的霍普金森压杆示意
在高压气体作用下冲头以一定的速度冲击入射杆,在入射杆中产生入射应力波,该应力波传递到试件端面时一部分通过试样进入透射杆,另一部分反射回入射杆,通过贴在前后杆上的应变片可以测出入射波、反射波以及透射波的信号.采用适用于脆性材料数据处理的“三波法”[14]对采集到的应变信号进行处理,即可得到特定应变率下试样应力-应变关系:
(1)
(2)
(3)
式中:Ae、As分别表示弹性杆和试样的横截面积;Ee表示弹性杆的弹性模量;Ce和Ls分别表示弹性杆的纵波波速和试样的长度;εI(t)、εR(t)、εT(t)分别表示入射、反射以及透射波应变信号.
若试样中应力均匀化、无衰减,引入输入杆和输出杆中的应变关系εI(t)+εR(t)=εT(t),则上式可通过“二波法”[15]表示如下:
(4)
(5)
(6)
1.3 试验方案
为了达到循环冲击的目的,试验开始前需要对试样进行试冲以确定合适的冲击荷载,从而防止试样被一次冲坏.试冲时先固定子弹在发射腔中的位置不变,然后调整气压值对试样进行试冲.最终确定的入射波应力幅值分别为110,90,70和50 MPa.每一种冲击速度选取3~5个试样,以保证至少能得到3个有效数据.试验时,将黄油均匀地涂抹在试样两端以减小岩样和弹性杆的摩擦,从而降低端部效应的影响.
与单次冲击相同,循环冲击试验过程中试样也需要满足应力均匀性假设[16].图3为C1试样在第4次冲击过程中的应力均衡图,可以看出,入射波与反射波之和与透射波曲线在峰值应力之前基本重合,说明试样中的应力已达到均衡状态.

图3 动态应力均衡图
2 试验结果分析
表1为部分试样的力学参数和试验结果,其中D1、D2和D3试样在冲击了20次之后均未发生宏观破坏.限于篇幅,仅选择代表性试样进行分析.所谓代表性试样为相同弹速下距平均循环冲击次数最为相近的试样.据此,仅对A1、B1、C1、D1试样进行分析.
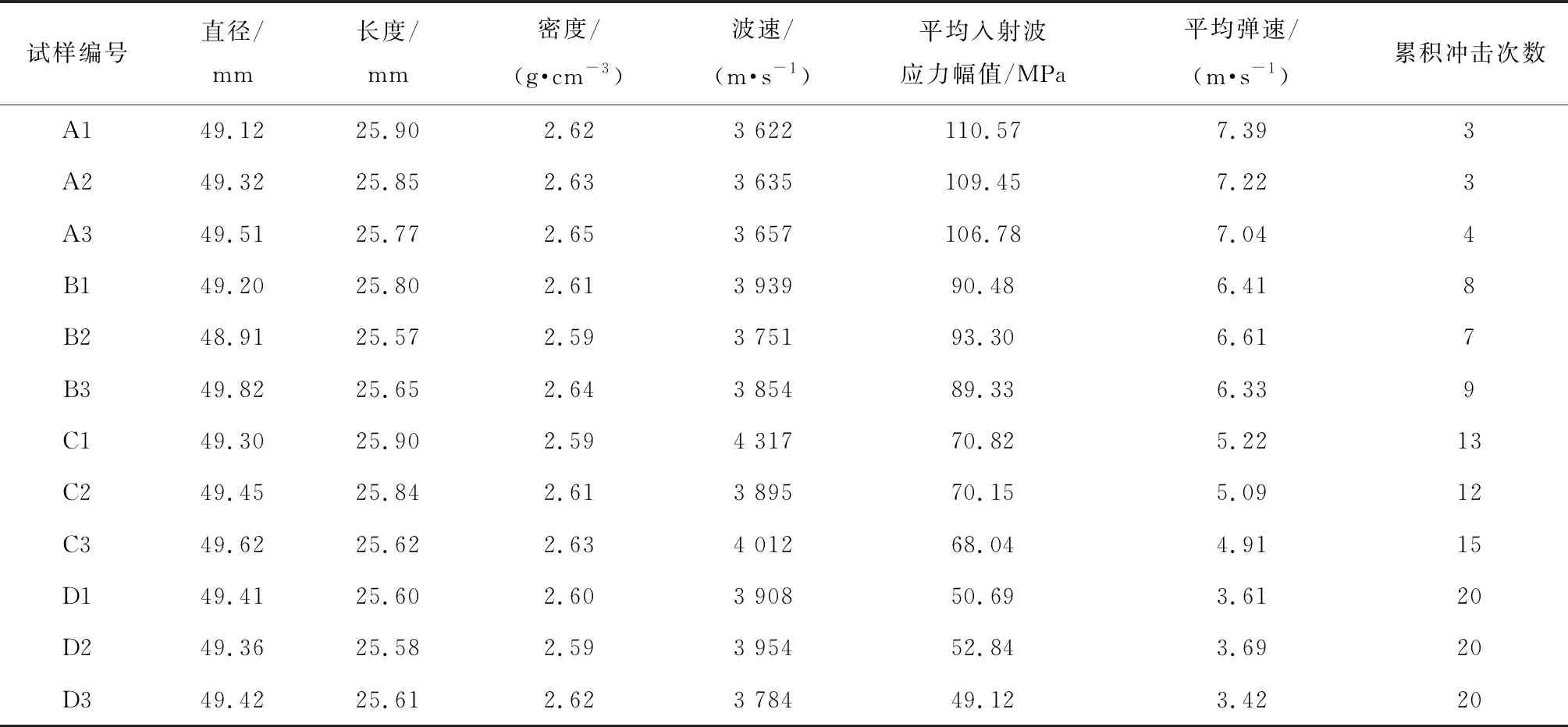
表1 花岗岩试样的力学参数和试验结果
2.1 原始波形图分析
图4为A1和D1试样的循环冲击原始波形.可以看出,每次冲击波的入射波幅值基本一致,达到等幅循环冲击的要求;随着冲击次数的增加,A1试样的反射波峰值逐渐增大,而透射波峰值逐渐减小.根据式(5)可知,反射波越大其对应的应变率就越大;根据式(6)可知,透射波越小其对应的试样应力就越小.故A1试样的平均应变率随着冲击次数的增加而不断增大,而峰值应力则在不断降低,反映出试样的损伤在逐渐增大.与A1试样原始波形图形成鲜明对比的是,D1试样的反射波峰值和透射波峰值在经历20次循环冲击之后,并未发生明显的变化.

图4 循环冲击原始波形
2.2 应力-应变曲线
图5为试样在不同循环冲击荷载下的应力-应变曲线.定义加载段的最大应力为峰值应力,应变所达到的最大值为最大应变.由图5可知,当试样未破坏时,在峰值应力之前,应力-应变曲线的变化趋势较为相似,大致可以分为两个阶段,起初都是一个近似的直线段,之后曲线进入非线性变形阶段,曲线的斜率逐渐减小.峰值应力后,应力-应变曲线都有一定程度的回弹,试样没有表现出宏观破坏,故卸载段会释放所储存的部分弹性能.

图5 循环冲击荷载下的应力-应变曲线
2.3 峰值应力与循环冲击次数的关系
峰值应力随循环冲击次数的变化如图6所示.可以看出,入射波应力幅值为110.57和90.48 MPa时,A1和B1试样的峰值应力均随着冲击次数的增加而持续减小,表现为承载能力的持续劣化.根据一维应力波理论[12],应力波在两种不同的介质中发生反射与透射时,存在以下关系:
(7)
σR(t)=FσI(t),
(8)
(9)
σT(t)=(1+F)(1-F)σI(t).
(10)


图6 峰值应力与冲击次数的关系
随着循环次数的增加,岩石内部的损伤不断增加,试样的波阻抗不断减小,导致反射系数F不断减小,其绝对值不断增加.由式(10)可知,若不考虑应力波在试样内的多次透反射,当入射波保持恒定时,透射波不断减小.因此,试样A1和B1的峰值应力随着冲击次数的增加而不断减小.入射波应力幅值为70.82 MPa时,在第7次冲击之前C1试样的峰值应力逐渐增大,之后其峰值应力又逐渐降低.分析认为,前7次冲击所产生的损伤总体上小于试样内微裂纹的闭合量[17],压密作用占据主导地位,所以,岩石的波阻抗逐渐增大,进而使得透射波越来越大,故前7次的峰值应力是不断增大的.随后,冲击损伤软化作用使得岩石内部损伤不断累积,岩石的波阻抗不断减小,峰值应力逐渐降低.与前3个试样不同的是,D1试样的峰值应力在经历20次循环冲击之后,并没有发生明显下降,其峰值应力在56 MPa上下浮动,间接地说明了岩石的波阻抗基本没有变化,内部损伤不甚明显.
2.4 最大应变与平均应变率的变化规律
试样在冲击过程中最大应变和平均应变率的变化规律如图7,8所示.可以看出,最大应变和平均应变率随冲击次数的变化规律较相似,原因是它们都代表着岩石的变形能力.其中A1和B1试样的最大应变和平均应变率随着冲击次数的增加而逐渐增大,这是因为岩石波阻抗的降低导致反射系数F的绝对值增大,通过式(8)可知反射波在逐渐增大,相应的应变率也就越大;岩样的变形能力不断减弱,故最大应变和平均应变率随着冲击次数的增加而不断增大.C1试样的最大应变和平均应变率则呈现出先减小后增大的趋势,这是由压密作用导致的岩石波阻抗先增大后降低引起的.而D1试样的波阻抗基本没有变化,所以,在相同的冲击荷载下其最大应变和平均应变率没有明显的变化.
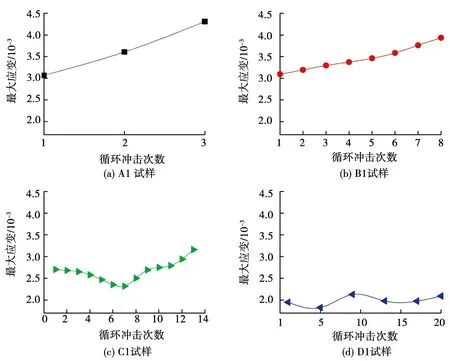
图7 最大应变与冲击次数的关系

图8 平均应变率与冲击次数的关系
2.5 花岗岩损伤演化规律
为了探究循环冲击下花岗岩的损伤演化规律,通过下式来定义损伤[8,18]:
(11)
式中En为第n次冲击后岩石的弹性模量.
从岩样冲击载荷下的应力-应变曲线可以看出,压密段并不明显,峰前表现出较好的弹性变形,故本文弹性模量采用下式计算:
(12)
式中:σ表示轴向应力,ε为轴向应变,下标1和2分别对应应力-应变曲线峰值40%和60%的两个点.
图9为试样在循环冲击过程中损伤度D随冲击次数的变化,可以看出,不同冲击荷载下花岗岩表现出不同的损伤演化规律.A1试样的损伤近似呈线性增长,而且损伤累积速度大于其他3种情况;B1试样的损伤则先增长较快然后趋于稳定;对于C1试样,由于压密作用使得前7次的冲击产生了负损伤,第7次冲击过后其损伤值达-0.25;之后内部裂隙加速扩展、贯通,所以,其损伤累积速度加快并且迅速上升为正值,最后破坏时其损伤值为0.22;D1试样在经历了20次冲击后其损伤值只有0.05,而且其损伤值一直在较小的范围内波动,并没有出现增长的趋势,所以,产生的损伤可以忽略不计.
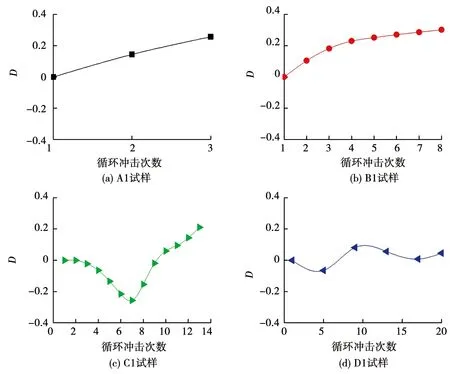
图9 试样损伤与冲击次数的关系
2.6 循环冲击下岩石损伤应力阈值
由图6可知,与单次冲击下峰值应力随入射波应力幅值的增加而增加相同,循环冲击荷载下试样首次冲击时的峰值应力亦随着入射波应力幅值的增加而增加,即加载率效应.当入射波应力幅值分别为50.69,70.82,90.48和110.57 MPa时,试样首次冲击时的峰值应力分别为56,81.8,105.7和131.2 MPa.在进行岩样疲劳试验时,葛修润等[19]发现周期疲劳荷载下岩样存在一个疲劳破坏门槛值,该值细观上对应岩石试件开始发生裂纹萌生的应力状态;卢高明等[20]也指出当岩石试样受到的上限应力大于该疲劳破坏门槛值时,岩石内部损伤不断累积,且疲劳寿命随着上限应力的增加不断减小;当试样受到的上限应力小于该疲劳门槛值时,岩石内部未有明显损伤产生.从前面分析可看出,试样首次冲击时的峰值应力越大,力学性能劣化越快,试样的损伤累积速度越快;当试样首次冲击时的峰值应力为56 MPa时,岩石内部没有明显损伤产生.因此,可以认为在SHPB循环冲击荷载下,同样存在一个裂纹起裂应力值.
Brace等[21]和Bieniawski[22]发现了低孔隙度岩石无侧限和受限试验的应力-应变曲线中有4个关键点,分别是轴向应变中的裂纹闭合点、侧向应变中的裂纹起裂点、体积应变中的非稳定裂纹增长点以及轴向应变的峰值点.Nicksiar等和Martin[23-24]在对岩石做了大量静态压缩试验后,发现利用岩石静态压缩应力-应变曲线可以得出其裂纹起裂应力值、非稳定裂纹增长应力值和峰值应力值,又叫“侧向应变响应法”,其主要步骤如下:(i)通过体应变曲线的反弯拐点,确定出裂纹非稳定增长的起始应力值;(ii)在轴向应力和侧向应变曲线上,连接侧向应变0点和裂纹非稳定增长的起始应力点,可得侧向应变的参考线;(iii)计算出侧向应变曲线和参考线之间的差值,用ΔLSR表示;(iv)绘制轴向应力和ΔLSR之间的曲线,并利用抛物线方程进行最佳拟合;(v)依据所得到抛物线上侧向应变差的最大值,确定出静态裂纹起裂应力值.
本文所研究的华山花岗岩试样的静态压缩应力-应变曲线如图10所示.采用上述方法,从图10的轴向应力-体积应变曲线上判读出体积应变的最大点作为此岩石的非稳定裂纹增长点,对应的应力值为96.4 MPa,而轴向应力-轴向应变曲线的峰值应力等于144.8 MPa.图11给出了利用侧向应变响应法确立裂纹起裂应力过程,可见此花岗岩的静态裂纹起裂应力值约为60.1 MPa.据此可知静态裂纹起裂应力与静态压缩强度的比值为0.415.

图10 花岗岩静态压缩应力-应变曲线
梁昌玉等[25]的研究表明,岩石的裂纹起裂应力和峰值强度均随着应变率的增加而增加,但岩样的起裂应力和峰值强度的比值与应变率无明显的相关性.由此,近似提出动态起裂应力的计算式如下:
(13)

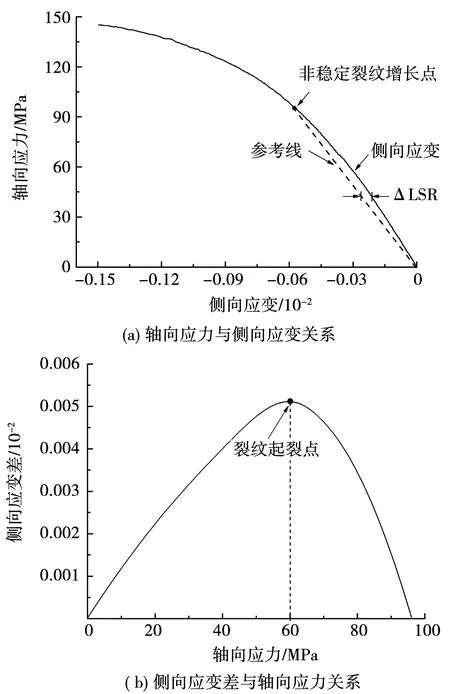
图11 利用侧向应变响应确立裂纹起裂应力
Fig.11 Evaluation of crack initiation stress using lateral strain response
3 结 论
1)入射波应力幅值为110.57和90.48 MPa时,随着冲击次数的增加,其峰值应力逐渐降低,最大应变与平均应变率则相反;入射波应力幅值为70.82 MPa时,初始几次冲击会使岩样中部分裂纹闭合,整体处于压密阶段;当入射波应力幅值降为50.69 MPa时,岩样的力学性质基本没有明显变化.
2)不同循环冲击荷载下试样呈现不同的损伤演化规律,入射波应力幅值为110.57和90.48 MPa时,损伤累积速度较快;入射波应力幅值为70.82 MPa时,损伤值先降为负值之后又快速增长为正值;而入射波应力幅值为50.69 MPa时,试样内部产生的损伤较小,可忽略不计.
3)由于SHPB冲击压缩试验中难以准确获取试样的侧向应变信号,本文把基于静态压缩应力-应变曲线推求到的裂纹起裂应力,乘以一个强度放大比例系数,从而发展出特定应变率下的岩样动态裂纹起裂应力的近似确定方法,结果能较好地解释循环冲击试验中观测到的现象.
