不同冲击荷载下花岗岩力学和能量耗散特性

贾帅龙，王志亮，巫绪涛，黄佑鹏

(合肥工业大学 土木与水利工程学院，合肥 230009)

随着社会经济不断发展，中国土木建筑行业发展迅速，新建工程项目数量日益增多.许多工程领域中的问题均涉及岩石在动荷载下的动力学特性及破坏问题，例如隧道开挖、矿山开采和爆炸防护工程等.岩石动态加载下的力学性质表现特征和破碎能耗演化过程是非常复杂的.由于动载荷的作用时间很短，岩石的动载强度与静压强度有很大不同，破碎能量也会发生变化，用静压强度去估计和衡量岩石动力破碎的难易程度会有较大误差.因此，开展冲击载荷下岩石动力学行为与能量耗散特性的研究，具有重要的理论意义和实用价值.

近年来，许多学者对岩石的动力性能展开研究：刘军忠等[1]采用分离式霍普金森压杆(SHPB)对角闪岩的动态力学性能进行了研究，指出抗压强度与比能量随应变率的增加而近似线性增加；李晓锋等[2]分别对灰岩、白云岩和砂岩进行动态冲击试验，并在此基础上结合晶体离散方法研究了材料高应变率力学和损伤特性；甘德清等[3]对磁铁矿石进行冲击压缩试验，发现磁铁矿石吸能效率随入射能的增加呈先增大后稳定的变化趋势；平琦等[4]对砂岩冲击进行SHPB压缩试验，得出砂岩的破碎耗能密度与入射能呈线性正比关系；Hong等[5]为确定岩石动态性能与应变率的关系，选择花岗岩、砂岩和石灰石进行冲击压缩试验，指出能量耗散密度与动态强度具有良好的对数关系；刘少赫等[6]在围压下对砂岩进行了循环冲击试验，并采用波速定义损伤，发现砂岩的应力、应变特征与波速之间存在良好的相关关系；许金余等[7]对斜长角闪岩、绢云母石英片岩和砂岩在不同围压和循环冲击作用下动态力学进行研究，并通过理论建立岩石损伤的判断标准，指出累积比能量吸收参量能较好描述岩样的损伤程度；朱晶晶等[8-9]分析了砂岩与花岗岩在冲击荷载下力学特性和损伤规律，发现损伤度随应变的增加逐渐增大，累积损伤增量主要由最后一次冲击破坏造成；Li等[10]对花岗岩进行中等应变率下的SHPB试验，发现应变率对弹性模量影响不大，应变率的增加使岩石吸收率增大，破坏程度增大.

综上，目前岩石动力特性研究已取得不少成果，但以往对岩石动力特性的研究多集中在应力-应变曲线峰前阶段和动态抗压强度等方面，而对应变率曲线特征以及应力-应变曲线峰后阶段行为的研究尚不多见.本文拟采用SHPB对黑云母花岗岩进行单次和重复冲击压缩试验，首先考察能量耗散对试样破坏形态的影响，然后探讨应变率曲线的变化规律，最后对应力-应变曲线特征进行分析，力求得出具有参考价值的结论.

1 试验准备

1.1 试样制备与弹速确定

试验采用的黑云母花岗岩试样取材湖南汨罗地区，岩样外观呈灰白色，属于中细粒黑云母花岗岩.该花岗岩的平均密度为2 600 kg/m3，主要含微斜长石(38%)、斜长石(29%)、石英(21%)与黑云母(7%)等矿物成分.试样经取芯机取样后进行切割，为满足应力均匀性要求，试样尺寸选为φ50 mm×25 mm，即高径比取为0.5[11]，如图1所示.试件两端面平整，不平行度控制在0.05 mm以内，以免岩样在加载过程中受到偏压造成应力集中而影响试验结果[12].

试验设计为单次和重复冲击两种加载方式，通过固定子弹位置并调节冲击气压来控制弹速.为确定单次冲击合理的弹速值，先对试样进行预冲击，以试样破裂并有碎片出现作为冲击弹速最低临界值，由此确定单次冲击的5个弹速分别为12.5，13.6，15.2，16.8和18.6 m/s；对于重复冲击试验的弹速，确立依据是首次冲击后试样须完好，且试样承受的最大重复冲击次数限定在30次以内，依此选定4个弹速为7.2，8.5，10.0和11.5 m/s.为降低测试数据的离散性，每种弹速准备3个试样，并取接近测试数据平均值的试样进行分析.

图1 花岗岩试样

1.2 试验装置

SHPB装置见图2，主要由子弹(撞击杆)、压杆(入射杆和透射杆)、吸收杆及缓冲器组成.撞击杆、入射杆和透射杆的长度分别为400，2 400和1 800 mm.压杆采用高强度合金钢制成，波速为5 172 m/s，弹性模量为210 GPa.在高压气体作用下子弹以一定速度v撞击入射杆产生入射应力波，当应力波传到试样与入射杆接触面时，试样发生变形，一部分应力波发生反射，形成反射波；另一部分应力波透过试样进入透射杆形成透射波.这些应力波通过贴在入射杆和透射杆上的应变片进行记录.

图2 SHPB装置

根据试样与压杆的界面条件以及一维应力波理论，试样的应变率、应变和应力计算如下[13]

(1)

(2)

(3)

式中：εi、εr、εt分别为入射波、反射波和透射波应变信号，E为压杆弹性模量，A、As分别为压杆和试样的横截面积，c为压杆波速，ls为试样长度.

2 试验结果分析

2.1 应力均匀性验证及动态压缩曲线

试验过程中，在试样两端涂抹凡士林，以降低杆件与试样之间摩擦.为保证试样在加载过程中达到应力均匀，在入射杆撞击端面中心位置粘贴直径10 mm、厚度1 mm的橡胶片作为波形整形器(见图2)[14].图3(a)、(b)分别为单次冲击与第3次重复冲击(共5次)下试样的动态应力曲线，其中符号In、Tr和Re分别代表入射波、透射波与反射波，入射波均为整形后波形，入射波上升和下降沿趋势较缓，且没有明显的波形震荡现象.此外，通过对比可知，入射波和反射波之和与透射波在峰值前基本吻合，表明试样在加载过程中达到了动应力平衡.

图3 试样动态应力平衡图

图4为试样单次冲击下应力时程曲线，可以看出，不同弹速下入射波曲线形状比较相似，且入射波峰值随弹速的增加而增大，但透射波差别较大.图5为试样重复冲击弹速v为10.0 m/s时的应力时程曲线，可以看出，入射波曲线基本重合，说明每次冲击下弹速比较稳定.

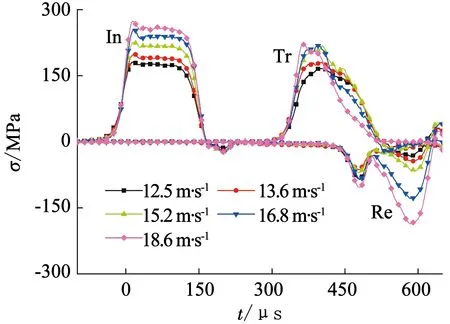
图4 单次冲击下应力时程曲线

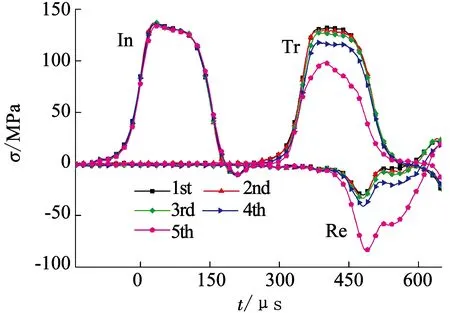
图5 重复冲击下应力时程曲线

2.2 单次冲击下试验结果分析

2.2.1 能量特性与破坏形态

岩石试样在冲击荷载作用过程中发生破碎，其吸收的能量主要转化为破碎耗散能和弹射动能.根据文献[15]的研究成果可知，大部分吸收能量耗散于岩石试样的断裂破坏，因此，可用吸收能近似替代破碎耗散能.为了分析冲击荷载下岩石试样的能量特性，定义比能量(ASE)为单位体积岩石吸收能[7]：

(4)

(5)

式中：WL为试样吸收能，Vs为试样体积，E、A和c意义同前.

表1列出了单次冲击下的弹速、入射波峰值应力、应变率及比能量数值，其中试样编号中首个数字“1”代表单次冲击.可以看出，随着弹速的增加，入射波峰值应力、应变率和比能量都呈逐渐增大的趋势.

表1 单次冲击下花岗岩参数与试验结果

图6为单次冲击下比能量与应变率的关系，可以看出，比能量随应变率的增加而增加，表现出较强的线性关系.图7显示了动态抗压强度与比能量的关系，通过拟合可发现动态抗压强度与比能量呈现对数函数关系，因此，比能量在一定程度上可以反映出动态抗压强度的变化趋势.当应变率较小时，试样的破损较小，弹性阶段吸能较大，因此，强度随比能量增加而增大较快；随应变率增大，试样后期破损严重，消耗大量能量，强度随比能量增加而趋于稳定.

图6 比能量与应变率的关系

图7 动态抗压强度与比能量的关系

Fig.7 Relationship between dynamic compressive strength and specific energy

图8为单次冲击下试样的破坏形态.可以看出，试样破坏程度随比能量的增加而增大，由块状变为细粒状.由于试样在冲击荷载作用下，获得的能量将以材料内部裂纹萌生、扩展和贯通的形式耗散，因而破坏程度与比能量有关.在比能量较大时，更多的裂纹被激活并汇聚贯通，当累积裂纹密度达到某一阈值时，导致岩石材料发生粉碎性破坏；而比能量较低时，岩样内部裂纹数量相对减少，破碎块体较大.

图8 单次冲击下试样破坏形态

2.2.2 应力-应变曲线特征

图9为不同弹速单次冲击下试样的应变率曲线.可以看出，应变率曲线出现“双峰”特征，该现象主要与试样破碎程度有关.当试样破碎严重时，岩石性能发生显著变化，与杆件波阻抗严重不匹配，导致应力波大部分反射回入射杆，因此形成第2波峰，其能较好反映出试样的破碎程度[16-17].随着入射波峰值应力的增加，第2波峰值逐渐增大，同时应变率降低为负值时间由180 μs增加到210 μs，表明试样峰值应变和破坏程度逐渐增大.

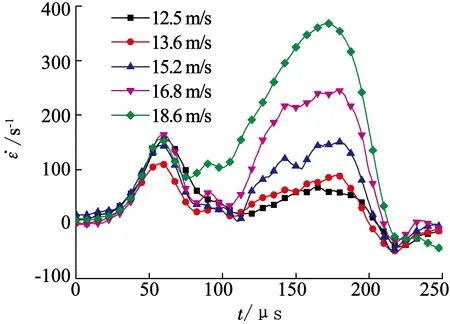
图9 不同弹速下应变率历时曲线

Fig.9 Strain-rate history curves under different impact velocities

图10为单次冲击下试样的应力-应变曲线.可以看出，在加载阶段中后期，曲线斜率逐渐减小，表明试样内部裂纹不稳定传播扩展，产生塑性变形，传递荷载能力逐渐降低.当应变率较小时，曲线峰后阶段应变随应力的降低而减小，出现回弹现象，这主要因为试样破坏程度较小，试样仍具有一定承载能力，部分能量在峰后释放.当应变率较大时(如170.0/s)，峰后段应变继续增加，对应的应力逐渐降低，试样失去承载能力.

图10 单次冲击下应力-应变曲线

2.3 重复冲击下试验结果分析

2.3.1 能量与破坏形态

探讨重复荷载作用下岩石的力学特性，有助于正确认识岩体的破坏机理，进而科学地评价岩体的长期稳定性.为了分析重复冲击下花岗岩的能量特性，定义累积比能量[8]：

(6)

式中：ASEi为第i次冲击下的比能量；n为冲击重复次数.

表2列出了入射波峰值应力、冲击次数、累积比能量及试样破坏程度，其中试样编号首数字“2”代表循环冲击.可见当入射波峰值应力为92.8 MPa时，试样在30次重复冲击作用下的累积比能量为0.82 J/cm3，但未发生破坏，这是因为入射波峰值应力低于静态抗压强度的60%，每次冲击不会对试样造成损伤[10].随着入射波峰值应力的增大，冲击荷载导致试样损坏加剧，试样能承受的重复冲击次数逐渐减少.当累积比能量为1.42 J/cm3时，试样破碎块数较多，而当累积比能量为0.66，0.70 J/cm3时，试样分别破裂为3块和5块，由此可知试样破坏程度随累积比能量的增加而增大(图11).

图12为不同弹速重复冲击下峰值应力与累积比能量随冲击次数的变化.可以看出，不同弹速下，随着冲击次数的增加，峰值应力逐渐降低，而累积比能量逐渐增大.这主要由于冲击荷载作用下，岩石内部原始裂纹由于应力集中起裂，且随着冲击次数的增加累积比能量增加，导致更多的裂纹扩展贯通，形成宏观裂纹引起岩样断裂，因此，岩石承载能力逐渐降低.同时，随着冲击次数的增加，整体上累积比能量的增加幅度逐渐增大，比能量呈现出增大的趋势，说明随着冲击次数的增加，试样吸能逐渐增加，当达到一定程度时，吸能快速增加导致试样发生破坏.

表2 重复冲击下花岗岩参数与试验结果

图11 重复冲击下试样破坏形态

图12 不同弹速下试样峰值应力与累积比能量变化

Fig.12 Variations of peak stress and accumulative specific energy under different impact velocities

2.3.2 应力-应变曲线特征

图13为不同重复弹速下应变率曲线.可以看出，应变率持续增长时间为60～70 μs，之后开始逐渐降低.随着冲击次数的增加，应变率峰值逐渐增大，同时应变率降低为负值的时间逐渐增加，表明峰值应变逐渐增大.当重复弹速v为10.0 m/s时，第4冲击下的应变率峰值与第5次相差较大，应变率曲线由“单峰”向“双峰”转变，且试样破坏程度较大(图11(b)，ϑ=1.42 J/cm3)；而当重复弹速v分别为11.5和8.5 m/s时，随着冲击次数的增加，应变率曲线始终表现为“单峰”特征.且试样破坏程度较低，分别破裂为3块(ϑ=0.66 J/cm3)和5块(ϑ=0.70 J/cm3)，如图11(a)、(c)所示.这主要因为试样未发生破坏或破坏程度较小时，材料性能变化较小，应力波大部分通过试样透射到透射杆上,而只有一小部分反射回入射杆，应变率曲线不足以形成第二“波峰”.而当试样破坏程度较大时，由于材料性能的显著变化，应力波大部分反射回入射杆，导致应变率曲线出现“双峰”特征.因此，试样在最后一次冲击破坏下，应变率曲线特征可以表明试样破坏程度.

图13 不同弹速重复冲击下应变率历时曲线

Fig.13 Strain rate history curves of repeated impact under different impact velocities

图14为不同弹速重复冲击下试样的应力-应变曲线.可以看出，当试样未发生破坏时，应力-应变曲线基本分为弹性加载、损伤演化和峰后回弹3段.处于弹性加载阶段时，表现为应变随应力的增加而近似线性增加；当加载段由直线逐渐转变为曲线时，表明试样产生损伤，微裂纹不稳定增长和传播；卸载阶段，试样弹性变形逐渐恢复，应力-应变曲线出现回弹现象.同时，随着冲击次数的增加，回弹线与加载包络线面积有增大趋势，说明试样损伤逐渐加剧.随着试样损伤的累积，其弹性加载段逐渐变短，直接进入损伤演化阶段，试样裂纹不稳定扩展并逐渐贯通，导致试样发生破坏.

图14 不同弹速重复冲击下应力-应变曲线

Fig.14 Stress-strain curves of repeated impact under different impact velocities

应力-应变曲线峰后阶段形状与试样破坏形态有关，例如弹速v为11.5 m/s时，试样破裂为3块(见图11(a))，卸载阶段仍有一部分弹性能释放，因此，峰后阶段出现回弹现象.然而，当弹速v为10.0 m/s时(见图11(b))，试样破坏较严重，已失去承载能力，峰后阶段应力随着应变的增加而持续降低.此外，前者破坏程度小于后者的原因前面已阐述，即11.5 m/s弹速冲击下试样的累积比能量要小于10.0 m/s的(分别为0.66和1.42 J/cm3).

根据以上可知，试样应力-应变曲线峰后阶段形状与吸收能量有关.单次冲击下，比能量随着应变率的增加而增加，试样破坏程度逐渐加剧.因此，应力-应变曲线峰后段的回弹现象将逐渐减弱，应变软化特征逐渐明显.重复冲击下，能量是逐渐累积的过程，应力-应变曲线峰后段大多出现回弹现象.当试样发生破坏时，随着累积比能量的增加，试样破坏程度逐渐增大，应力-应变曲线峰后段回弹现象渐弱，出现应变软化现象.

3 结 论

1)单次冲击下，试样破坏形态与比能量有关，随着比能量的增加，试样破坏程度逐渐增大，由块状变为细粒状；重复冲击下，损伤累积到一定程度试样发生破坏，且破坏程度随着累积比能量的增加而加剧.

2)单次冲击下，应变率曲线出现明显的“双峰”特征，且随着入射波峰值应力的增加，第2峰逐渐高于第1峰；重复冲击下，随着冲击次数的增加，应变率曲线的峰值逐渐增大，当试样破坏严重时，应变率曲线由“单峰”向“双峰”过渡.

3)单次冲击下，入射波峰值应力较低时，应力-应变曲线峰后阶段表现出明显的回弹现象，随着入射波峰值应力的增加，试样破碎程度加剧，峰后回弹现象消失；重复冲击下，试样破坏前每次冲击的应力-应变曲线基本经过弹性加载、损伤演化和峰后回弹三阶段，而试样发生冲击破坏时，应力-应变曲线峰后阶段特征与其破坏程度相关.