基于BP人工神经网络的聚能射流速度预测方法

2020-03-20黄鸿鑫张会锁岳晓媛

火炮发射与控制学报 2020年1期

黄鸿鑫，张会锁，张帆，岳晓媛，王蒙

(中北大学机电工程学院，山西太原 030051)

聚能装药战斗部主要用来击毁坦克、装甲车辆和混凝土构筑工事等。由于聚能装药战斗部是依靠金属药型罩形成的金属射流来击毁目标的，它对发射平台提供的初速要求不高，可适用于多种武器平台。聚能装药战斗部是目前用得最多、最广泛的一种战斗部形式[1]。

随着现代装甲结构的发展和防护能力的提高，要求聚能装药战斗部，尤其是中、大口径聚能装药战斗部能对各种目标有足够的侵彻能力以及相应的后效作用，能够破坏目标内部机构、杀伤乘员，使目标失去作战能力。要提高聚能装药战斗部的威力，其形成的射流速度必须要足够高，但影响射流速度的因素又是多方面的，很难用一般函数的表达式来表示，引入神经网络方法则可以有效地解决这个问题。国内外对射流速度的研究大多都是试验研究或者是数值仿真，试验研究通常耗资巨大且得到数据具有一定的局限性；数值仿真虽省时省力且计算精度也可以基本达到要求，但是数值仿真总要经历建模划分网格和设置各种初始条件以及边界条件等过程，特别是针对一些多因素影响分析时，改变其中一个变量，整个数值仿真的过程又必须重新进行。笔者为了克服这两者之间的局限性，利用数值仿真得出数据，导入人工神经网络，通过对数据的反复测试训练，最终得出计算精度较为准确的计算模型，该计算模型可以实现对金属射流速度快速而又准确的预测。

1 数值模拟

1.1 计算模型

聚能装药几何模型示意图如图1所示。

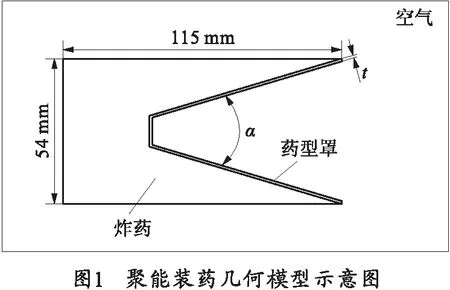
在相同装药尺寸的情况下，分别设计出厚度t为1.0、1.5、2.0 mm,锥角α为30°、42°、60°的药型罩，药型罩的材料均为紫铜；炸药分别采用TNT、OCTOL、B炸药。

建立空气、炸药和药型罩3个部分的2D仿真模型，均采用欧拉算法。同时为了避免模型边界对计算结果的影响，在整个模型4个边加上流出边界，整个欧拉域中单个网格的尺寸为0.5 mm，网格数量为120 000.

1.2 材料模型

炸药分别为TNT、OCTOL、B炸药，均采用JWL(Jones-Wilkins-Lee)[2]状态方程。该状态方程在炸药爆轰过程及爆炸驱动的数值模拟中广为采用，JWL等熵方程为

(1)

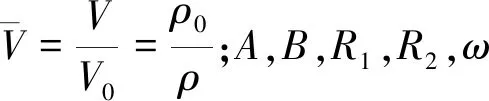
(2)

使用Mie-Gruneisen状态方程描述气体的一般运动，有：

(3)

将式(1)和式(2)代入式(3)，令Γ=ω，得到JWL一般压力形式：

(4)

式中：E=ρ0e为单位初始体积内能；A,B,R1,R2,ω等是由实验确定的参数，本文均使用AUTODYN材料库中参数，如表1所示。紫铜采用Johnson-Cook[3]本构模型，也均使用AUTODYN材料库中默认参数，具体材料参数如表2所示。

表1 炸药材料参数

表2 紫铜材料参数

该本构模型为了模拟承受大应变、高应变率材料的强度性能，此模型定义屈服应力为

σY=(A+Bεn)(1+Clnε*)(1-T*m)，

(5)

(6)

式中：ε为有效塑性应变；ε*=ε/ε0,为无量纲应变率(ε=l s-1,为参考应变率)；Tr为参考温度(室温)；Tm为材料熔点；A，B，n，C，m为材料常数；T*为相似温度。

1.3 欧拉算法

在欧拉算法中，计算网格固定在空间上，不能随着物体移动，而材料相对于网格运动，因此不存在网格畸变问题。各时刻的速度、压力、密度和温度等物理量是在空间点上计算，而不是像拉格朗日算法那样在物质点上计算，因此质量、动量和能量等物理量将跨越单元边界在单元间运输。各单元的体积在计算过程中保持不变，但单元质量由于输运而不断发生变化。欧拉算法比较适合模拟大变形问题，因此在计算流体力学中多采用欧拉算法，早期用于爆炸冲击问题的流体动力学程序也多采用欧拉算法[4]。由于射流的形成过程和炸药爆轰过程属于高度非线性问题，存在大变形和大位移，若采用拉格朗日算法可能会造成网格畸变最终导致计算终止，所以笔者将使用欧拉算法来避免网格畸变。

1.4 数值仿真结果与数据提取

射流最终形态如图2所示，因篇幅有限，只显示厚度、角度、炸药等典型画面。从数值模拟得到的结果可以看出，药型罩厚度较大时，形成射流的杵体部分占药型罩质量的比率较大；药型罩锥角增大时，杵体部分容易与射流部分分离。数值模拟结果如表3所示。

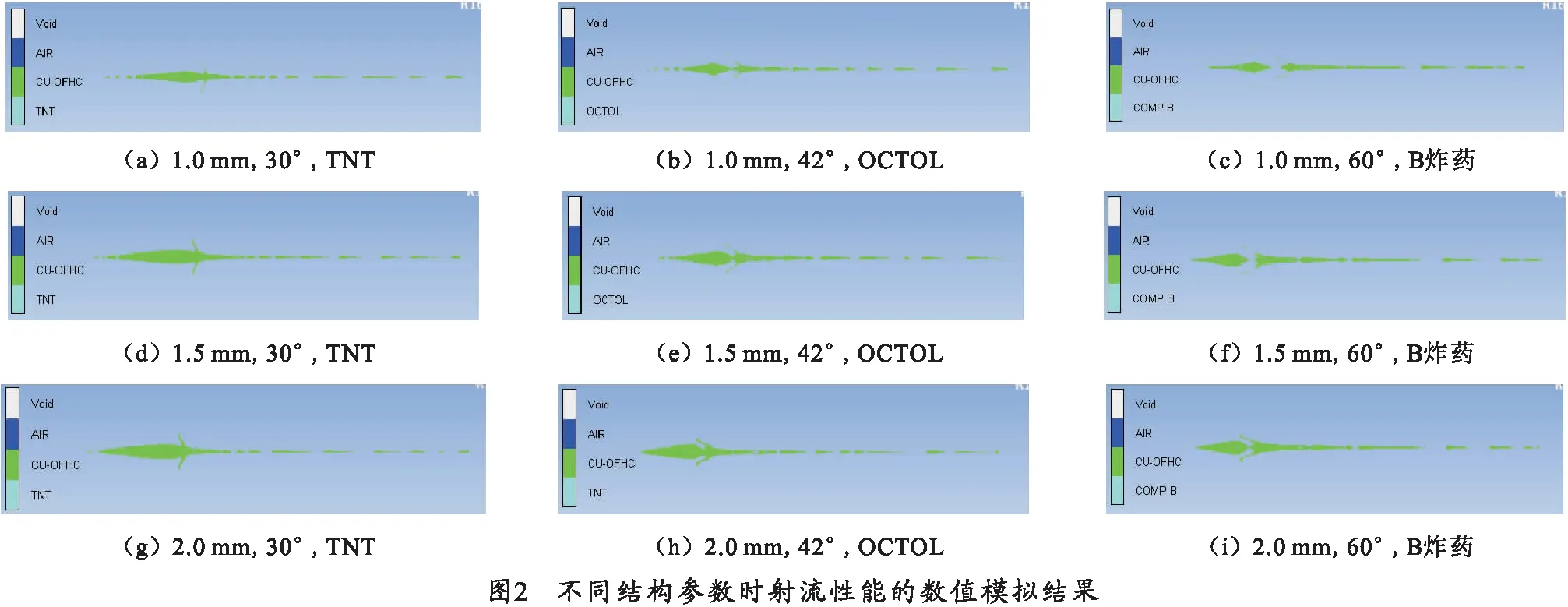
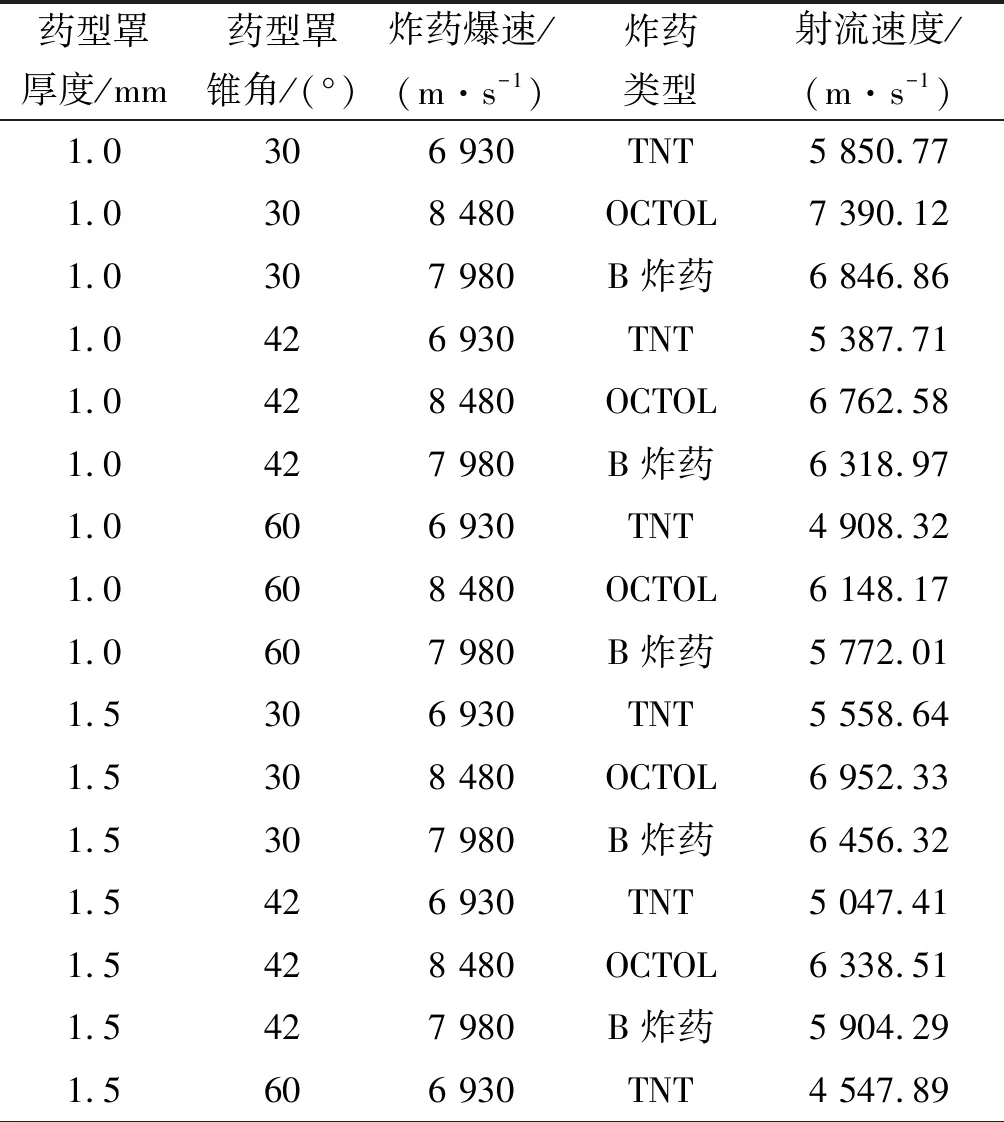
表3 27组聚能装药形成射流的速度(数值模拟结果)

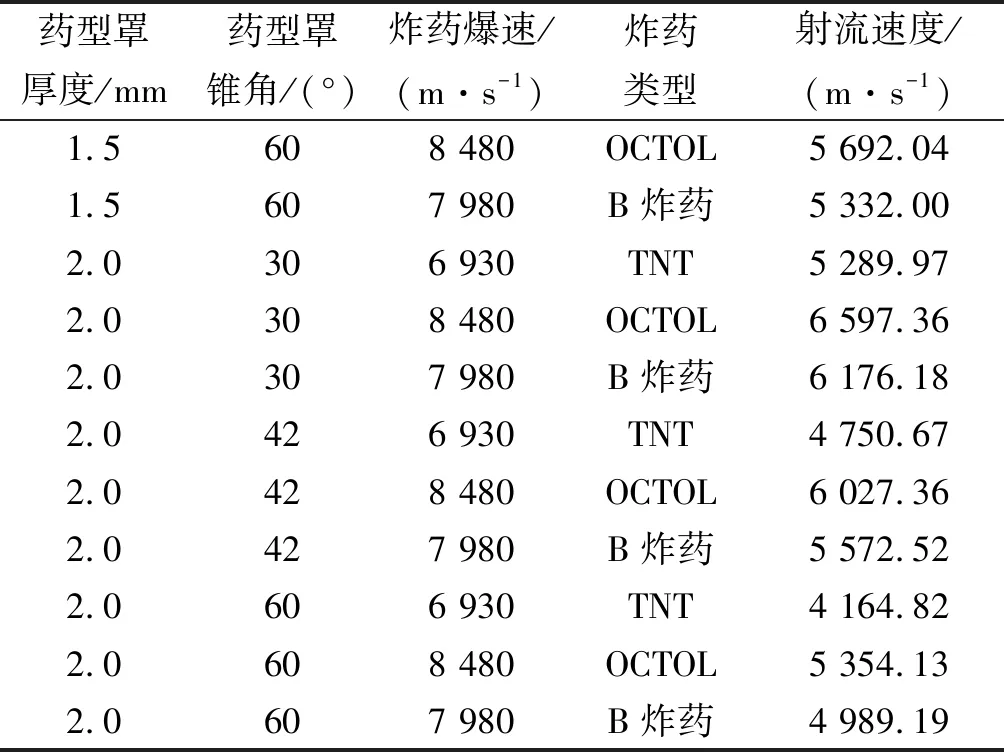
表3(续)

射流速度最大的一组是药型罩厚度为1.0 mm、锥角为30°、炸药采用OCTOL；速度最低的一组为药型罩厚度为2.0 mm、锥角为60°、炸药采用TNT.3种因素均对射流速度有较大影响，但炸药的爆速是影响射流速度最重要的因素。在相同壁厚和锥角的情况下，聚能装药采用TNT和OCTOL分别形成的射流速度相差近约20%；而药型罩厚度对射流速度的影响只有4%，药型罩厚度在1.0～2.0 mm范围内时，射流速度随着厚度的增大而减小；锥角的大小对射流速度的影响约为9%，锥角在30°～60°范围内时，射流速度随着锥角的增大而减小；所以在搭建神经网络时，对于炸药类型的这个测试因子需着重考虑。

2 BP人工神经网络搭建与仿真结果

2.1 BP人工神经网络学习算法

BP人工神经网络是一种多层前馈神经网络[5]，该网络的主要特点是信号前向反馈，误差反向传播。在前向传递中，输入信号从输入层经隐含层逐层处理，直至输出层。每一层的神经元状态只影响下一层神经元状态。如果输出层得不到期望输出，则转入反向传播，根据预测误差调整网络权值和阈值，从而使BP神经网络预测输出逼近期望输出。BP人工神经网络的拓扑结构如图3所示。

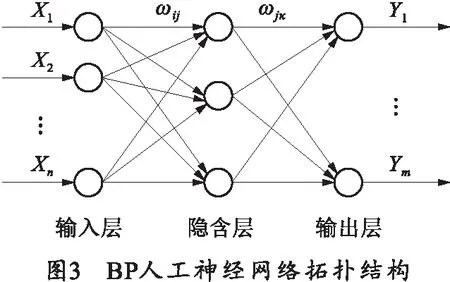
其中X1，X2，…，Xn是BP神经网络的输入值，Y1，Y2，…，Ym是BP神经网络的预测值，ωij和ωjk为BP神经网络权值。将药型罩厚度、药型罩锥角和炸药类型作为神经网络的输入值，射流速度作为神经网络的预测值。为了加快网络的学习效率，一般需要对原始数据的输入和输出数据进行归一化处理，目的是为了消除各维数据之间数量级差别，避免因为输入输出数据数量级差别较大而造成网络预测误差较大。笔者所采用归一化的方法为最大最小法[6]，其函数形式如下：

Xk=(Xk-Xmin)/(Xmax-Xmin)，

(7)

式中：Xmin为数据序列中的最小数；Xmax为数据序列中的最大数。

随后将归一化完成的数据输入到隐含层内计算。根据输入变量X，输入层和隐含层间连接权值ωij以及隐含层阈值a，计算隐含层输出H:

(8)

式中：l为隐含层节点数；f为隐含层激励函数，该函数有多种表达式，所选函数为

(9)

根据隐含层输出H，连接权值ωjk和阈值b，计算BP神经网络预测输出O：

(10)

根据网络预测输出O和期望输出Y，计算网络预测误差e：

ek=Yk-Ok，k=1,2,…,m.

(11)

网络预测误差e更新网络连接权值ωij、ωjk：

(12)

ωjk=ωjk+ηHjek，

(13)

式中：i=1,2,…,n；j=1,2,…,l；k=1,2,…,m；η为学习速率。

然后根据网络预测误差e更新网络阈值a、b：

(14)

bk=bk+ek.

(15)

2.2 仿真分析

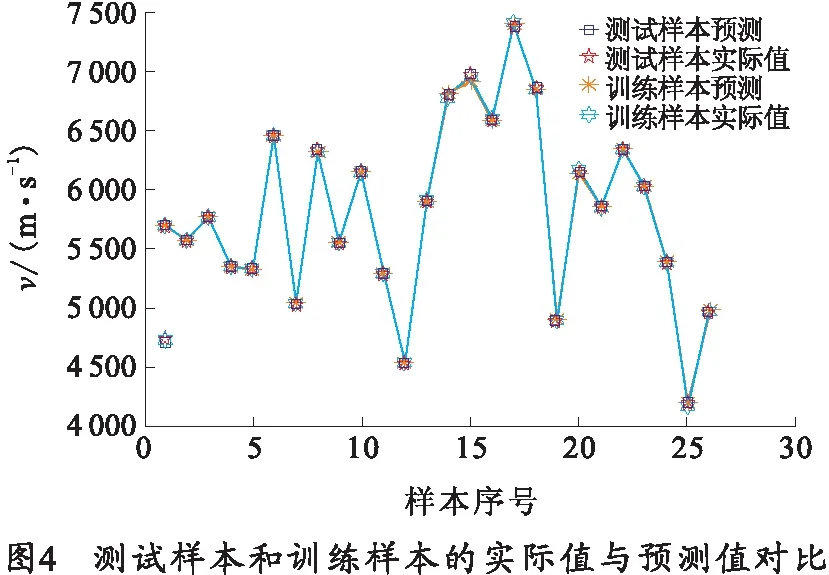
设置药型罩锥角分别为30°、42°和60°，药型罩厚度分别为1.0、1.5和2.0 mm，炸药分别为TNT、OCTOL和B炸药。将27组数据分为26个训练样本和1个测试样本，为保证训练质量，调整参数方式选择梯度下降法，并反复调整训练有关的相关参数，最终结果如图4所示。从图4可以看出，不论是训练样本还是测试样本，最终的预测值已经与实际值十分接近。若样本进一步增大，得到的结果几乎可以与测试样本完全吻合。

为了验证笔者所建立的BP神经网络的准确性，再次利用有限元分析AUTODYN模拟出表4数据并与BP神经网络的预测值进行对比。从表4可以看出，BP预测值与数值模拟仿真值吻合情况较好，这就意味着网络最终的预测误差不会因样本数量的变化而发生变化。且BP神经网络在保证准确性的前提下，其运行效率远远高于一般有限元分析软件的运行效率。尤其是对一些高度非线性问题，使用人工神经网络可以大大提高工作效率，精确度也是可以保证的。