基于等参数线的B样条曲面类型识别方法
2020-03-19徐静,董雁
徐 静,董 雁
(1.绍兴文理学院 元培学院,浙江 绍兴 312000;2.绍兴文理学院 机械与电气工程学院,浙江 绍兴 312000)
0 引言
随着造型软件的广泛应用,三维模型检索成为一个新的研究热点。形状大小不同的功能相似零件,其表面组成和空间位置关系往往相同或相似,因此零件三维模型大多利用边界表示模型的拓扑结构信息,利用面的类型、边的凹凸性等信息构造表面属性邻接图,再通过图匹配算法对零件三维模型进行检索[1]。由于计算机辅助设计(Computer Aided Design,CAD)模型中除了平面、圆柱面、圆锥面、球面等规则曲面外,其余表面均表示为(有理)B样条曲面,这些B样条曲面形状差异大,检索相似零件时需要进一步细分[2]。
根据高斯曲率和平均曲率符号,Sunil等[3]将自由曲面分类为峰、凹、脊、谷、平面、极小曲面、鞍状脊和鞍状谷;根据曲面变形的自由度,Pernot等[4]将自由曲面分类为半自由曲面、自由曲面和完全自由曲面;Gupta等[5]用二元分类法对自由曲面进行分类,第一元根据分割线与基本曲面边界线间的关系将曲面分为双盲、盲、通道、闭环、巢等,第二元通过分析基本曲面主曲率符号将曲面分为凹、凸、鞍和平面。上述分类方法粒度较大,为此He等[6]引入多元分类方法,首先按整体形状将自由曲面分为扁平、凹或凸、带状、扫描曲面、球状、柱状、锥状、尖角状、扭曲状和复合状,再按生成方式、特征曲线类型和曲面的拓扑结构对每个子类进行分类,这样的分类较细,但分类过程繁琐,需要人工干预,结果往往非常复杂。
线具有明确的结构约束和形态内涵,是点和面的中间层,在曲面中具有承上启下的作用,它包含了可以联系底层的点和上层的面之间重要的造型信息,却没有点的繁琐和面的冗余。因此,学者们普遍采用曲线作为编辑自由曲面特征的基本单元,再通过定义面向设计用户的直观参数来控制曲线的形状,通过曲线的变化实现对自由曲面特征的控制[7-8]。
在反求工程领域,经区域分割后,需要识别潜在平面、圆柱面等规则曲面并提取几何参数,这类规则曲面的类型大多通过曲线来识别。例如,Lai等[9]将回转面视为平面曲线绕轴线做回转运动生成的曲面,将曲面重构问题转化为以轴线和平面曲线的B样条控制点为参数的非线性最小二乘问题;Andrews等[10]在分析三维空间单参数运动群速度矢量性质的基础上,引入极大似然法来识别运动生成曲面,避免了算法的坐标系依赖问题。
上述方法主要侧重于点云数据的研究,能识别的曲面类型仅局限于运动生成曲面。在造型软件中,自由曲面定义为B样条曲面,其等参数线往往包含了曲面的定义曲线,因此可以通过等参数线的类型、组成及其之间的空间位置关系对曲面进行分类识别,这样的分类识别方法同样适用于运动生成曲面。
本文首先讨论了平面等参数线的类型识别问题,然后对B样条曲面中U向和V向等参数线之一为平面曲线的空间等参数线,用平面等参数线族的空间位置关系确定柱面曲线的母线方向和回转面曲线的回转轴线,将空间曲线识别为柱面曲线和回转面曲线,对于还不能识别的空间等参数线,通过最小二乘法进行圆柱(锥)面拟合,最后利用等参数线的组成、族内部及其之间的几何位置关系对B样条曲面进行类型识别。
1 等参数线的类型识别
1.1 平面等参数线的拟合
从Pro/E随书光盘下载5万个有效零件模型,通过整体码比对排除相同结构零件[11],得到22 623个零件模型,其中包含B样条曲面的模型有7 969个。在这7 969个模型中,B样条曲面的数量为306 226,其中U向和V向等参数线均为平面曲线的B样条曲面有164 141个,之一为平面曲线的有121 786个,均为空间曲线的有20 299个,分别占306 226个B样条曲面的53.60%,39.77%,6.63%,可见零件模型B样条曲面的等参数线大多数为平面曲线。之一为平面曲线的B样条曲面,其空间曲线的拟合见1.2节。均为空间曲线的B样条曲面归类为空间等参数线B样条曲面。平面等参数线拟合的基本流程如图1所示。

若控制顶点数为2,等参数线为直线,则离散点数取2,否则取两倍控制顶点数减1;考虑到三次曲线拟合有10个待定系数,至少需要10个插值点,若离散点数大于3且小于10则取10。均匀离散参数域,得到等参数线离散点。
以起始点为原点,由起始点和与其距离最大的点做直线,即为X轴,提取与该直线距离最大的离散点及其距离,用该离散点确定Y轴,构建局部坐标系,如图2a所示。若该距离与直线长度的比值(相对直线弓高)小于阈值,则判断为直线;若直线长度小于阈值,则判断为点。提取与XY平面距离最大的离散点及其距离,若该距离与直线长度比值(相对直线弓高)小于阈值,则判断为平面曲线。判断为点、直线、平面曲线及曲线拟合的阈值均为0.000 1,实例如图2b所示。
平面二次曲线方程的一般形式为
Ax2+Bxy+Cy2+Dx+Ey+F=0。
(1)
平面二次曲线存在直角坐标变换下的不变量,因此可利用不变量进行曲线分类[12]。排除点和直线情形后,平面实二次曲线的判定如表1所示,表中不变量的含义如下:
I1=A+C;
(2)
I2=AC-B2;
(3)
I3=ACF+BDE/4-(AE2+CD2+FB2)/4。
(4)


表1 平面实二次曲线的判定
平面二次曲线的拐点数量为0,因此先计算等参数线离散点的拐点数,若拐点数量为0,则通过最小二乘法求待定系数判定平面二次曲线的类型。
为了避免式(1)只有零解,参考文献[13]的思路,分别规定二次项系数A,B,C为1,取误差最小的拟合方案,并确定拟合曲线的参数值。中心型曲线的中心点坐标、长短轴半径和长轴斜率,非中心型曲线的顶点坐标、焦参数和主方向斜率的计算可参考文献[12]。
下载模型的平面等参数线中存在不能判定为点、直线和平面二次曲线的曲面数为24 803,占B样条曲面总数的8.14%,不同拐点数量出现的频次如表2所示;参考平面二次曲线拟合的思路,分别规定三次项系数为1,取误差最小的拟合方案,还不能成功拟合为三次曲线的曲面数为412,不同拐点数量出现的频次如表3所示。

表2 非平面二次曲线不同拐点数量出现的频次

表3 非平面二、三次曲线不同拐点数量出现的频次
1.2 空间等参数线的拟合
U向和V向等参数线之一为平面曲线的B样条曲面占比达39.77%,存在如螺旋面包含的圆柱(锥)螺旋线这样有工程意义的空间曲线,需要进一步识别。有工程意义的空间曲线往往位于柱面或回转面上,因此空间曲线的识别可分为柱面曲线识别和回转面曲线识别两类。
柱面曲线识别需要先确定柱面母线方向:通过平面等参数线族所在平面是否平行或存在公共垂面、直线族是否平行或存在导平面,确定是否可识别为柱面曲线,若可以,则将空间等参数线离散点沿该方向投影到平面上,按1.1节方法进行拟合。
根据轴线是否已知,可将回转面曲线识别细分为两类:
(1)通过平面等参数线中平面曲线(直线)族是否存在共交轴线来确定是否可识别为回转面曲线,若可以,则将空间等参数线离散点沿轴线回转方向投影到平面上,按1.1节方法进行拟合。
(2)通过最小二乘法求待定系数进行圆柱(锥)面拟合,拟合方法为:令轴线的基点坐标为(x0,y0,z0),方向矢量为(l,m,n);对于圆柱面拟合,基点和方向矢量各分量中各只有两个独立,分别取一基点矢量分量为0,方向矢量分量为1,规定半径待定系数为R;对于圆锥面拟合,取基点为锥顶,取一方向矢量分量为1,拟合点到锥顶和到轴线的比值为R。
圆柱螺旋线在柱面曲线识别中的投影曲线为圆,在回转面曲线识别中的投影曲线为直线,圆锥螺旋线在回转面曲线识别中的投影曲线也是直线,进一步识别这类典型空间曲线的曲线类型。
空间等参数线平面二次曲线拟合实例如图2所示,拟合结果如表4所示。表中给出的曲面总数为满足形成方法的曲面数量,拟合数为投影到平面后能识别为二次曲线的数量,每栏有两种形成方法,数据用“+”号分隔,因为圆锥面拟合成功的很少,所以最后一栏只给出圆柱面的拟合数据。平面曲线(直线)族共交轴线中投影方法为“平行投影”给出的拟合数据是沿轴向投影到平面后能识别为二次曲线的数量,投影方法为“周向投影”给出的拟合数据是沿轴向投影不能识别,但沿轴线周向投影到平面后能拟合为二次曲线的数量。

表4 空间等参数线平面二次曲线拟合数量
由表4可见, U向和V向等参数线之一为平面曲线的B样条曲面数为121 786,可以借助平面等参数线得到投影方法的曲面总数为79 029,识别成功的曲面数为46 177,分别占121 786个B样条曲面数的64.89%和37.09%。因此利用平面等参数线族的几何位置信息可以大大提高空间等参数线识别算法的效率和成功率。
2 等参数线的空间位置关系
2.1 等参数线族内部几何位置关系的确定
平面等参数线族的内部几何位置关系及其符号表示如表5所示。构成平行关系的直线族存在公共垂面,这样的直线族构成了共垂直平面关系。存在公共平行平面的直纹曲面称为柱(锥)状面,公共平面称为导平面,其母线组成的直线族构成了共平行平面关系。直线族若位于同一平面上,则构成共面关系。将构成共平行平面关系且不共面的直线族投影到导平面上,判断是否进一步构成共交线关系。构成共交点关系的为锥面。不能判断为上述几何位置关系的直线族,通过最小二乘法求待定系数判断是否构成共交线(相切圆柱面)关系,拟合方法为:将直线族的两两方向矢量叉积,根据叉积矢量的平均分量从大到小排序,得到主方向序号;将直线族投影到主方向为法线的平面上并两两求交,取交点的平均分量为初始点;取主方向上的基点矢量分量为0,方向矢量分量为1,以主方向序号优先顺序进行拟合计算。

表5 平面等参数线族的内部几何位置关系及其符号表示

续表5
若平面曲线位于同一平面上,则构成共面关系,相互平行的平面曲线族构成共平行平面关系,对于由圆、椭圆和双曲线这类中心型曲线组成的平行平面曲线族,分析中心点坐标是否在同一轴线上,判断是否进一步构成同轴关系。将构成共垂直平面关系的平面曲线族投影到公共垂面上,判断是否进一步构成共交线(相切圆柱面)关系,对于中心型曲线,分析中心点坐标是否在公共交线上,从而判断是否进一步构成点在线上关系。
同一等参数线族有时会出现同时包括两项内部几何位置关系的情形。例如,直线等参数线族构成共平行平面关系,将其投影到导平面上后判断为共交线关系,这时内部几何位置关系同时包括共平行平面关系和共交点关系,记为∥xN;当中心型平面曲线等参数线族构成共交线关系且中心点坐标在公共交线上时,内部几何位置关系同时包括点在线上关系和共交线关系,记为oLxL。
识别的空间曲线族包括柱面曲线族和回转面曲线族两大类,其内部几何位置关系根据投影的平面曲线和轴线定义。
判断为平行和垂直关系的角度阈值为±1°,判断为共面关系、公共交点、线和圆柱面的阈值为0.001。不能判断为上述几何位置关系的称为空间一般关系。限于篇幅,等参数线族内部几何位置关系的图例在第4章结合实例分析给出。
2.2 等参数线族间几何位置关系的确定
根据包含的等参数线类型,等参数线族分为直线、平面曲线和空间曲线3类,分别用1D,2D,3D标记。常见的等参数线类型为点、直线、圆(弧)、椭圆(弧)、双曲线、抛物线、平面三次曲线、未识别平面曲线、柱面曲线、回转面曲线、圆柱螺旋线、圆锥螺旋线和未识别空间曲线,分别用p,l,c,e,h,a,i,u,t,r,cs,os,v标记。平面三次曲线和未识别平面曲线在基本符号后标记拐点数量,拐点数量为0时省略标注。柱面曲线和回转面曲线在基本符号后标记投影平面曲线的类型,其中回转面曲线还需标记投影平面曲线与回转面轴线之间的空间位置关系。
等参数线族内部几何位置关系中的共交点关系包含公共交点;共面关系、平行关系、共平行平面关系、共垂直平面关系、共母线方向的柱面曲线包含公共方向矢量;同轴关系、共交线关系、共相切圆柱面关系、共回转面轴线曲线包含公共轴线。这样等参数线族间的几何位置关系可以通过公共交点、公共方向矢量和公共轴线关系来描述,几何位置关系及其符号表示如表6所示,其中xN标记两公共交点重合,oL标记公共交点在轴线上,⊙,∥,⊥,?分别标记两个公共轴线(方向矢量)为同轴、平行、垂直和一般空间关系。限于篇幅,等参数线族之间几何位置关系的图例在第4章结合实例分析给出。

表6 等参数线族之间的几何位置关系及其符号表示
平面等参数线族内部几何位置关系和等参数线族间几何位置关系的统计数据如表7和表8所示。

表7 平面等参数线族内部几何位置关系统计数据

表8 等参数线族之间的几何位置关系统计数据
3 B样条曲面类型的识别
3.1 B样条曲面的编码
基于等参数线的B样条曲面结构码格式为“等参数线族之间几何位置关系码、等参数线族1结构码、分隔符、等参数线族2结构码”,其中的分隔符为“:”。
等参数线族结构码的格式为“等参数线族类型码、族内部几何位置关系码和等参数线类型字符串”。在等参数线类型字符串中,等参数线类型由各自的符号表示,相邻相同类型的等参数线只需表达一次,并以p,l,c,e,h,a,i,u,t,r,cs,os,v优先选择次序确定是选择正序还是逆序等参数线类型字符串。
为了保证结构码的唯一性,两个等参数线族按直线、平面曲线和空间曲线排序;当等参数线族类型相同时,按等参数线族内部几何位置关系,即共面关系、垂直共面、平行共面、同轴关系、相交共点、相交共线、相切共面、点在线上、一般关系排序;当等参数线族内部几何位置关系相同时,按等参数线类型字符串排序。图2b~图2i模型中指定曲面的结构码分别为∥2D∥cp:2DxLe;∥2D∥c:3D⊙tc(∥2D∥c:3D⊙cs);∥2DxLc:3D⊙te;∥1D∥l:3D⊙tc(∥1D∥l:3D⊙cs);∥1D⊥l:3D⊙tc(1D⊥l:3D⊙cs);⊙2DxLc:3D⊙roLc;⊙1DxLl:3D⊙r∥l(⊙1DxLl:3D⊙cs)和?1D?l:3D?r∥l。
3.2 基于结构码的B样条曲面类型识别
对下载模型中包含的306 226个B样条曲面,经等参数线类型识别和空间位置关系确定并编码,得到不同曲面结构码的数量为2 153,其中不同等参数线族结构码的数量为757。
根据统计学理论,正态分布曲线中基区占68.27%,为主体,此外95%(99%)展示了正态的全面性。将结构码按出现频次降序排序,分别取306 226个B样条曲面的68%,80%,90%,95%,100%,得到不同曲面结构码和等参数线族结构码的数量及其在全体结构码中的占比,如表9和表10所示。由表可见,虽然全体结构码类型较多,但是高频出现的结构码数量很少,因此曲面结构码和等参数线族结构码能有效用于B样条曲面类型识别。

表9 出现频次降序的不同曲面结构码数量
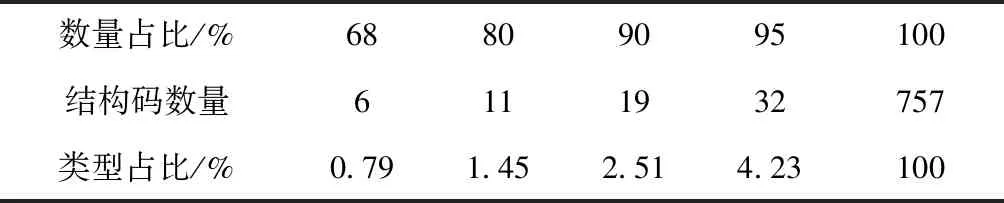
表10 出现频次降序的不同等参数线族结构码数量
基于结构码的B样条曲面类型识别有曲面结构码匹配和等参数线族结构码匹配两种方式,曲面结构码整体匹配能够识别出U向和V向等参数线族类型,以及两等参数线族内部及其之间几何位置关系均相同的B样条曲面。然而工程上有时仅需识别大类相同的曲面,例如螺旋面包括螺旋线,另一等参数线族类型与螺旋线族之间的几何位置关系可以不同;正圆柱面和斜圆柱面的U向和V向等参数线族类型及其内部几何位置关系均相同,但族之间的几何位置关系可以不同;圆柱面和椭圆柱面的U向和V向等参数线族之一分别为圆和椭圆。因此,可以采用指定等参数线族结构码,或者使用U向和V向等参数线族结构码均相同的两种方式对等参数线族结构码进行匹配。
图2c、图2e、图2f和图2h包括圆柱螺旋线族(3D⊙cs),其中图2c、图2e和图2f通过柱面曲线识别得到3D⊙tc,而图2h通过回转面曲线识别得到3D⊙r∥l,再进一步识别出圆柱螺旋线。图2f虽然也包括圆柱螺旋线族,但却是一个近似圆柱面,这类曲面结构码需要修正。
3.3 曲面结构码的修正
修正曲面结构码的基本思路是,利用曲面上与选定等参数线族正交的曲线族代替另一等参数线族并进行编码,作为曲面的结构修正码。为了保证修正码的有效性,选定的等参数线族和与其正交的曲线族应该是直线或平面曲线族,而且内部几何位置关系不能是空间一般关系。
存在共面关系的曲面识别为近似平面,不需要修正;构成共平行平面关系、共交线(相切圆柱面)关系的直线等参数线族的正交曲线族往往是空间曲线族或构成空间一般关系的平面曲线族,一般不选。因此,修正选定的直线等参数线族内部几何位置关系为共垂直平面关系和共交点关系。存在共垂直平面关系的直线等参数线族的曲面是近似柱面,其正交曲线族构成共平行平面或同轴关系;存在共交点关系直线的等参数线族的曲面是近似锥面,提取锥顶的等距曲线,判断是否为同轴圆(弧)且锥顶在轴线上,是则识别为近似圆锥面。
对于选定平面曲线等参数线族的情形,本文只讨论近似回转面的编码修正问题。修正选定曲线族的内部几何位置关系为同轴关系和共交线关系,且同轴关系的平面曲线均为圆(弧)。修正后族之间的几何位置关系为交线重合或点在线上,修正码为∥1D⊥l:2D⊙c;构成共交线关系曲线族的曲线类型必须相同,正交曲线族必须是同轴圆(弧),修正后族之间的几何位置关系为交线重合。
正交曲线族的提取方法如下:
(1)对于共垂直平面关系直线族,以需修正的直线(曲线)离散点在共垂直平面法线上投影点集的算术平均中点为正交曲线的构造平面与选定直线族求交,然后对交点集合进行曲线拟合,形成正交的曲线族。
(2)对于共交点关系直线族,以选定直线族的公共交点及需修正的直线(曲线)离散点到交点距离的算术平均值为正交曲线的构造球面与选定直线族求交,然后对交点集合进行曲线拟合,形成正交的曲线族。
(3)对于共交线关系且类型相同的平面曲线族,将以公共交线为法线方向的平面作为正交曲线的构造平面。将需修正的直线(曲线)族离散点向共交线投影,对投影点集区间按修正直线(曲线)族的数量均匀离散,得到构造平面族,令该平面族与选定平面曲线族求交,对各平面上的交点集合分别进行曲线拟合,形成正交的曲线族。
(4)对于同轴关系的圆(弧)曲线族,将过公共轴线的平面作为正交曲线的构造平面。构造平面族的形成方法为:以选定圆(弧)曲线族的中间曲线的起点定义平面族基准平面,将角度范围除以修正直线(曲线)族数,得到构造平面间的夹角增量,若需修正直线(曲线)的起止点超过了中间曲线定义的角度范围,则超过区域需添加构造平面。将平面族与选定圆(弧)曲线族求交,对各平面上的交点集合分别进行曲线拟合,形成正交的曲线族。
在(1)和(2)中,选定等参数线族为直线族,这时直接通过拟合的直线族与构造平(球)面求交点,作为曲面与构造平(球)面交线的离散点;在(3)和(4)中,选定等参数线族为平面曲线族,这时需要利用曲面离散点UV参数值以及点到构造平面的距离,应用线性插值的方法沿曲面等参数线迭代求解,得到等参数线与平面族的交点,作为曲面与构造平面交线的离散点。
曲面结构码的修正实例如图3所示,实例以原始编码命名,具体讨论如下:
(1)对于共垂直平面关系直线族,能识别为近似圆柱面的原始编码包括?1D⊥l:2D∥a,?1D⊥l:2D∥c,?1D⊥l:2D∥cec,?1D⊥l:2D∥e,?1D⊥l:2D∥h,?1D⊥l:2D∥i2,∥1D⊥l:2D∥c,∥1D⊥l:3D⊙tc,⊥1D⊥l:2D⊥c,⊥1D⊥l:2D⊥ac,⊥1D⊥l:2D⊥aca,⊥1D⊥l:2DxLece,⊥1D⊥l:2DxLac,⊥1D⊥l:2DxLc,修正码为∥1D⊥l:2D⊙c。
这类曲面原始编码的主要特征是待修正等参数线族的内部几何位置关系为平行关系时,族之间的几何位置关系为平行或空间一般关系;内部几何位置关系为垂直或共交线关系时,族之间的几何位置关系为垂直关系。
原始编码为?1D⊥l:2D∥e的情形如图3a所示,等参数线是构成共平行平面关系的平面曲线族,但与直线族之间为一般空间关系,正交曲线族为同轴圆弧,识别为近似圆柱面;原始编码为∥1D⊥l:3D⊙tc的情形如图2f所示,按1.2节柱面曲线识别方法得到的投影曲线与正交曲线误差不大;类似的情形为原始编码∥1D⊥l:3D⊙te和∥1D⊥l:3D⊙th,分别可识别为近似椭圆和双曲线柱面。

等参数线族之间的几何位置关系为垂直关系的实例有两种情况:①如图3b所示,平面等参数线的曲率半径很大,曲面较平坦,虽然定义平面变动较大,但是正交曲线的曲率半径仍然很大;②如图3c所示,平面等参数线族的平行误差为1.7°,超出阈值±1°不多,垂直误差为0.000 5°,判定为共垂直平面关系,正交曲线族的定义平面与这类曲面的等参数线所在的平面变动不大,因此也能成功识别。
选定共垂直平面关系直线族,也可能被识别为以椭圆(弧)、双曲线、抛物线为曲导线的近似柱面。例如原始编码为?1D⊥l:2D∥c时(如图3d),正交曲线族为同轴椭圆(弧),被识别为近似椭圆柱面,这类曲面的原始编码也存在近似圆柱面识别中类似的特征。
能识别为近似平面的原始编码包括?1D⊥l:1D?l,?1D⊥l:1D∥xNl,?1D⊥l:2DoLxLc,?1D⊥l:2DxLc,?1D⊥l:2D⊙c,?1D⊥l:2D∥c,∥1D⊥l:2DoLxLc,⊥1D⊥l:2D∥c,修正码有∥1D⊥l:1D∥xNl和⊥1D⊥l:1D⊥l两个,实例分别如图3e和图3f所示。从修正码可见,UV等参数线均为直线,而且等参数线族内部以及之间的几何位置关系同时包含∥和⊥,可以识别为近似平面,因此在曲面类型识别时,与包含共面关系的曲面一起归类为近似平面。
(2)对于共交点关系直线族,能识别为近似圆锥面的原始编码包括?1DxNl:2D⊙c和?1DxNl:2D∥c,修正码为oL1DxNl:2D⊙c。图3g和图3h分别是等参数线族的点在线上的误差为0.001 28、同轴误差为0.082 97,超出阈值0.001,这类修正曲面提取的正交曲线族与替换的等参数线族比较接近。
(3)对于共交线关系且类型相同的平面曲线族,能识别为近似圆环面的UV等参数线大多为平面曲线,原始编码包括?2DxLc:2D?c,?2D∥c:2DxLc,∥2D∥c:2DxLc,∥2D∥cp:2DxLc,∥2D∥ic:2DxLc,∥2D∥i12c:2DxLc,∥2D⊙e:2DxLc,∥2D⊙ec:2DxLc,∥2D∥e:2DxLc,∥2D∥ec:2DxLc,⊥2D⊥c:2DxLc,⊥2D⊥ec:2DxLc,修正码为⊙2D⊙c:2DxLc。从上述编码可见,等参数线族内部和之间的几何位置关系大多为∥和⊙,这类曲面的正交曲线是以公共交线为法线方向来构造定义平面,与曲面的等参数线所在平面变动不大。另一类几何位置关系是⊥,如图3i所示,等参数线族的平行误差1.7°超出阈值±1°,垂直误差为0.007°,判定为共垂直平面关系,等参数线族之间也是垂直关系,正交曲线族的定义平面与这类曲面的等参数线所在的平面变动也不大(略大于平行和同轴的情形),因此也能成功识别。
能识别为近似圆环面,且UV等参数线中包含空间曲线的原始编码包括∥2DxLc:3D∥tc和?2DxLc:3D?v,修正码为⊙2D⊙c:2DxLc;∥2DxLc:3D∥tc的情形如图3j所示;图3k和图3l分别表示?2DxLc:3D?v情形下的等参数线和正交曲线。从实例可见,包含空间曲线时等参数线和正交曲线之间的差异较大。
选定共交线关系且类型相同的平面曲线族,也可能识别为以椭圆(弧)、双曲线、抛物线、平面三次曲线,以及未识别平面曲线为母线的近似回转面。U向和V向等参数线族之间的几何位置关系均为平行关系,内部几何位置关系为共平行平面(同轴)关系。U向和V向等参数线大多为平面曲线,也存在包含空间曲线的情形,例如原始编码为∥2DxLe:3D∥tc和∥2DxLe:3D∥te的修正码均为⊙2DxLe:2D⊙c。
(4)对于同轴关系圆(弧)曲线族,能识别为近似圆锥面的原始编码有?1D?l:2D⊙c,?1DtCl:2D⊙c和?1DxLl:2D⊙c,修正码为oL1DxNl:2D⊙c,原始编码?1D?l:2D⊙c的修正实例如图3m所示,图中直线等参数线族虽然不能构成共交点关系,但是提取的正交曲线族为直线族且相交共点,因此识别为近似圆锥面,这类修正曲面等参数线族均包括直线族。
能识别为近似圆环面的原始编码包括?2D⊙c:2D?c,?2D⊙c:2D?e,?2D∥c:2D⊙c,?2D⊥c:2D⊙c,∥2D⊥c:2D⊙c,∥2D⊥e:2D⊙c,∥2D⊥h:2D⊙c,∥2D⊥a:2D⊙c,⊥2D⊙c:2D⊙c,⊥2D∥c:2D⊙c,⊥2D∥a:2D⊙c,修正码为⊙2D⊙c:2DxLc。这类曲面原始编码的主要特征是等参数线族内部的几何位置关系和之间的几何位置关系中,“∥和⊙”和“⊥”不会同时出现。等参数线族内部的几何位置关系为共垂直平面关系时,近似圆环面的环半径不大,若构成共平行平面(同轴)关系,则近似圆环面的环半径很大,因为前者正交曲线的构造平面与等参数线所在的平面变动不大,而后者变动很大,只有当等参数线为近似直线时才可能与正交曲线接近,从而能成功识别。图3n和图3o所示分别为原始编码∥2D⊥c:2D⊙c和⊥2D∥c:2D⊙c的图例。
同轴关系圆(弧)曲线族也可能被识别为以椭圆(弧)、双曲线、抛物线为母线的近似回转面,其修正码分别为⊙2DxLe:2D⊙c,⊙2DxLh:2D⊙c,⊙2DxLa:2D⊙c。原始编码∥2D⊥i3:2D⊙c的修正实例如图3p所示,其修正码为⊙2DxLh:2D⊙c。这类曲面原始编码也存在近似圆环面识别中的类似特征。
能识别为近似圆柱面的原始编码包括?1D?l:2D⊙c,?1D⊥l:2D⊙c,?2D⊙c:2D?c,?2D⊙c:2DxLc,?2D∥c:2D⊙c,?2D⊥c:2D⊙c,∥2D⊙c:2DxLc,∥2D⊙c:2DxLa,∥2D⊥c:2D⊙c,⊥2D∥c:2D⊙c,⊥2D∥i2:2D⊙c,修正码为∥1D⊥l:2D⊙c。原始编码?2D⊙c:2DxLc的图例如图4f所示。
4 实例分析
4.1 近似规则曲面的实例分析
在造型软件中,不定义为B样条曲面的规则曲面主要有平面、圆柱面、圆锥面、球面和圆环面。将位于等距距离小于给定阈值两等距规则曲面内的B样条曲面识别为相应类型规则曲面的近似曲面,近似规则曲面的识别方法如下:
(1)近似平面 根据曲面的全体离散点,按1.1节判断平面曲线的方法识别近似平面。
(2)近似球面 当曲率中心点和曲率半径离散度小于阈值时识别为近似球面。
(3)近似圆柱(锥)面 全体离散点的最大曲率半径均大于阈值,判断为直纹曲面并提取直母线方向;圆柱面的最小曲率半径、直母线方向平行误差离散度小于阈值,离散点沿直母线方向投影到平面上的轨迹为圆;圆锥面直母线的交点为锥顶,且最小曲率半径与该离散点到锥顶的距离成比例关系。
(4)近似圆环面 最大(小)曲率半径离散度小于阈值,进一步提取圆环的圆半径曲率的中心点集,若位于平面上且轨迹为圆,则识别为近似圆环面。
识别为近似平面的B样条曲面,其等参数线族内部的几何位置关系均为共面关系,族之间的几何位置关系为平行关系。当所包含的等参数线类型不同时,曲面结构码不相同,如图4a和图4b所示的结构码分别为∥1D|l:1D|l和∥1D|l:2D|e。在识别曲面类型时,将包含共面关系的曲面归类为近似平面。
能识别为近似球面的原始编码大多为⊙2D⊙c:2DoLxLc,其中2DoLxLc的含义是圆弧族共交线且圆心在交线上,如图4c所示。也存在原始编码为⊥2D⊙c:2D⊙c的实例,这类曲面较平坦(如图4d),其平均曲率半径为93.11,曲面包围盒的对角线距离为8.54,以对角线距离代替平均曲率半径计算阈值,不能识别为近似球面。
能识别为近似圆柱面的原始编码大多为∥1D⊥l:2D⊙c,占比达90%以上,如图4e所示。另外10%的曲面中有3成经修正可以得到上述编码,实例如图4f所示;不能修正的曲面编码为?2D⊙c:2DxLc和?2D⊙c:2D?c,实例如图4g所示,该实例曲面的平均曲率半径为3.63,曲面包围盒的对角线距离为3.31,圆柱面周长为1.16,以圆柱面周长代替平均曲率半径计算阈值,不能识别为近似圆柱面。

如图4h所示,能识别为近似圆锥面的原始编码近半为oL1DxNl:2D⊙c,其含义是直线族共交点且该交点位于同轴圆弧轴线上,剩余曲面的原始编码为?1DxNl:2D⊙c,均能修正得到上述编码。
近似圆环面的编码应该是⊙2D⊙c:2DxLc,然而实际得到数量最多的3个编码却是⊥2D⊙c:2D⊙c,⊙2D⊙c:2DxLc,⊥2D∥c:2D⊙c,在识别近似圆环面的过程中,分别用弦长代替圆环的回转半径和圆半径来计算阈值的效果不大。原因是等参数线族先判断共平行平面关系(角度阈值为±1°),不能识别时再判断共垂直平面和共交线关系。如图4j和图4k所示,当圆环面沿回转圆周的相对区域较小时,内部几何位置关系识别为平行(同轴)。
通过分析近似规则曲面的实例发现本文所提方法是有效的。
4.2 典型结构码曲面的实例分析
对下载模型中包含的B样条曲面经等参数线类型识别、空间位置关系确定、曲面编码和结构码修正,得到高频次出现的12类曲面结构码和10类等参数线族结构码,如表11和表12所示。对表11的曲面结构码,各提取300个零件模型实例。

表11 高频次出现的12类曲面结构码

表12 高频次出现的10类等参数线族结构码
将U向和V向等参数线族之一为直线族的曲面识别为直纹曲面。表11中有6类曲面为直纹曲面,所包含的直线族结构码分别为1D⊥l,1DxLl,1D|l,1D?l。由表12可见,除了1D|l外,其余编码均为高频出现的结构码。包含1D⊥l的曲面为近似柱面,其中∥1D⊥l:2D⊙c为近似圆柱面,∥1D⊥l:2D⊙e为近似椭圆柱面,∥1D⊥l:2D∥c为近似斜圆柱面,实例分别如图5a~图5c所示。∥1D|l:2D|c为近似平面,实例如图5d所示。⊙1DxLl:3D⊙r∥l的实例如图5e所示。


分析各自提取的零件模型可以发现,∥1D⊥l:2D⊙e,∥1D|l:2D|c,⊙1DxLl:3D⊙r∥l曲面形状的差异性较小,其中⊙1DxLl:3D⊙r∥l的实例大多为圆柱螺旋面。∥1D⊥l:2D⊙c存在如图5f所示的大曲率半径的实例,而∥1D⊥l:2D∥c几乎都是大曲率半径的情形。
将U向和V向等参数线族之一为圆弧族的曲面识别为圆纹曲面。表11中有8类曲面为圆纹曲面,所包含的圆弧族结构码分别为2D⊙c,2D∥c,2D⊥c,2DxLc,2D|c,2D?c,除了2D|c外,其余编码均为高频出现的结构码。⊙2D⊙c:2DxLc是近似圆环面,其实例如图5g所示。∥2D∥c:2DxLc,∥2D⊥c:3D∥te,?2D∥c:2D?c的实例分别如图5h~图5j所示,可见大多为过渡圆弧特征,其中∥2D∥c:2DxLc最接近圆环面。如图5k所示,∥2D⊥c:3D∥te也存在粗看像圆环的曲面,但仔细观察可以发现其管半径并不恒定。
表11中有5类曲面的UV等参数线族之一包含了空间曲线族。除了上面讨论的之外,图5l~图5n分别给出了?1D?l:3D?v,?2D?c:3D?v,?3D?v:3D?v的实例,从实例可见,识别等参数线族类型对区分这类复杂形状曲面是有效的。
若判断为平面曲线的阈值从0.000 1增大到0.002,则U向和V向等参数线均为平面曲线的B样条曲面有275 286个,之一为平面曲线的有29 558个,均为空间曲线的有1 382个,空间曲线族数量从162 384降低到32 322,平面曲线族达130 062,占80%。如图5o所示,当阈值为0.001 3时可以判定为平面曲线,因此可以通过分析近似平面曲线族进一步探讨包含空间等参数线族的复杂形状曲面类型识别问题。
5 结束语
针对自由曲面难以分类检索的问题,本文提出一种以B样条曲面等参数线为中心的曲面类型表示与识别方法,该方法先识别平面等参数线的类型,再利用平面等参数线族的内部空间位置关系确定空间等参数线的投影方向,将空间等参数线投影为平面曲线进行识别,最后利用等参数线的组成、族内部及其之间的几何位置关系对B样条曲面进行类型识别。相比于已有的研究成果,本文研究工作的特点表现如下:
(1)通过引入等参数线族内部及其之间的几何位置关系,拓展了如运动生成曲面这类能以曲线定义和表示的曲面种类。
(2)利用平面等参数线族的几何位置信息,可以大大提高空间等参数线识别算法的效率和成功率。
(3)本文所提方法算法简单、计算量小,分类过程无需人工干预。
实验结果表明,零件模型B样条曲面的等参数线大多为平面曲线,曲线类型容易识别。经过实例验证,所提的等参数线的类型识别、空间位置关系确定以及排序和编码方法等一系列算法是有效的。然而,对于UV等参数线均为空间曲线的B样条曲面(占零件模型B样条曲面的6.63%),本文方法不能进一步对其进行区分。
