考虑个体差异的系统退化建模与半Markov过程维修决策
2020-03-19蒋增强边靖媛
李 琦,李 婧,蒋增强,边靖媛
(北京交通大学 机械与电子控制工程学院,北京 100044)
0 引言
系统在完成本身预定功能的同时会受多种因素影响,这些影响造成了系统性能的缓慢退化。当系统的性能指标降低到一定阈值时,便无法保证其安全运行,应停止运行并进行系统(或部件)维修或替换。针对缓慢退化系统进行维修策略优化有两方面研究内容:①对系统的缓慢退化过程进行建模,寻找其内在规律;②根据退化规律进行维修策略优化,包括确定维修时间、维修方式和替换方法等。
近些年,学者们对缓慢退化系统的维护和更换问题进行了广泛研究。Love等[1]在半Markov决策过程(Semi-Markov Decision Process,SMDP)框架中分析了相关维修模型,考虑了可能发生故障的机器(系统)的状态特征,包括机器的真实役龄和已发生的故障数量;Castanier等[2]研究了可修复系统的连续监测退化状态维护策略,提出多阈值策略,利用维持系统状态的半再生(或Markov更新)特性构建了稳态下维护系统的随机模型;Leve等[3]研究了使用预防性维修策略和替换性维修策略来优化随机退化系统的维护问题,提出并分析了Markov决策过程模型,其维修目标是最大限度地减少预期折扣成本。可见,Markov过程是进行维护策略优化的重要技术框架。在计算方法方面,Moustafa等[4]采用了策略迭代算法,并对该算法和次优控制限制方法进行比较;Kim等[5]为了计算最优策略,开发了一种新的改进策略迭代算法,该算法使用Leve等[3]提出的嵌入式技术,减少了状态空间的计算量。
在Markov过程的框架内,诸多学者也在研究采样频率、退化规律建模等内容。Zhou等[6]采用基于蒙特卡洛密度投影方法将无限连续的状态空间映射到有限的“信念”状态空间中,然后在Markov决策过程中将其离散化,以确定最优维护策略;Wang等[7]研究了基于Weibull随机效应斜率和独立同分布误差项的线性退化模型,得出最优控制极限和监测间隔时长;Curcurù等[8]描述了具有漂移的一阶自回归模型的退化过程,并将其视为Markov退化过程;基于此,Tang等[9]提出利用具有时效性的自回归模型描述系统的退化过程,然后使用SMDP框架计算最优维护策略,并利用条件监测信息推导出缓慢退化的软故障系统的剩余寿命估算公式。由此可见,基于Markov决策过程(Markov Decision Process,MDP)及其分支理论SMDP的缓慢退化系统维修研究,正在向各个方向延伸完善,其中有关维修策略优化过程中遇到的采样不完全、采样成本高等问题的研究越来越切合实际。一般而言,解决这类问题需要据统计学原理,采用复杂的数学模型,其中适用于缓慢退化系统的基于SMDP的最优化维修策略模型是较为合适的方法之一,随着机器学习和人工智能的发展,该方法的求解算法逐渐成熟。
本研究采用基于SMDP的方法作为针对缓慢退化系统的退化过程进行最优化维修策略建模的技术框架。但是与以往研究不同的是,本研究着重考虑退化过程中不同个体的异质性,使用线性混合效应模型(Linear Mixed-Effects Model,LMEM)拟合分析缓慢退化系统的状态[10],既考虑总体退化的一般性(固定效应),也考虑个体退化的特殊性(随机效应)。据此求解状态转化概率,找到维修或替换策略的合理极限值,制定最优化维修策略,并最小化单位时间长期预计平均成本,从而使得系统效益最大化,推动系统向高可靠性方向发展。
1 半Markov决策过程基础理论
缓慢退化系统的状态维修是将连续的退化过程离散成有限的退化状态,通过检测判定系统所处的退化状态,从而采取相应的维修策略。描述离散状态退化过程的经典方法包括Markov决策过程、半Markov决策过程等。
1.1 Markov决策过程
设X(t)(t≥0)是取值在空间S={1,2,…,N}上的一个随机过程,若对任意自然数n及任意n个时刻点0≤t1 P{X(tn)=zn|X(t1)=z1,…,X(tn-1) =zn-1}=P{X(tn)=zn|X(tn-1) =zn-1},z1,…,zn∈E (1) 成立,则称X(t)(t≥0)是离散状态空间S上的连续时间Markov过程。若给定Markov过程X(t)(t≥0)当前所处的状态,则未来状态的转移只与当前状态有关,而与历史状态无关,这一特性称为Markov过程的无记忆性。MDP是基于Markov过程理论的随机动态系统的最优决策过程,决策者周期或连续地观测随机动态系统的状态,并依次做出决策。MDP主要包括状态s、行动a、状态转移概率P(s,a)、报酬R(s,s′,a)和目标V[11],因此可以用五元组{S,A(i),Pij(i,a),R(i,a),V}表示Markov决策过程。 由1.1节的定义可知,MDP只考虑各个状态之间的状态转移,忽略了系统在不同状态内的不同持续时间。然而,在实际系统运行过程中,系统在某一状态内往往会持续一段(不同的)时间,由此产生了SMDP,其与MDP的主要区别是考虑了设备处在各个状态的平均停留时间。 对平稳状态持续时间做如下定义:假设t1,t2,为半Markov随机过程X(t)(t≥0)的状态转移时刻,且满足0≤t1 图中,在状态S下,决策者可以选择任意一个行动a对系统做出决策;作为对行动a的响应,系统会根据一定的状态转移概率P(s,a),并经过一定的状态转移时间T(i,a)转移到一个新的状态S′,同时作为回报,系统会给决策者一个报酬R(s,s′,a)。在系统处于新状态S′的条件下,决策者会采取新的决策,并不断重复执行,直到系统在预设目标V下达到最优。 构建缓慢退化系统的SMDP模型时,系统状态往往以时间维度的退化数据来展现[12-13],目前常用的退化模型包括退化轨迹模型、退化量分布模型、Gamma过程模型、Wiener过程模型等[14],综合几种退化模型的特征可以发现:①这些模型在模拟时通常假设误差服从独立同分布,然而实际的观测数据很难满足这种条件,这种假设对估计结果有很大影响;②过去大多数模型关心的是研究对象的确定性模型和平均行为,忽略了个体之间或者群体之间的序列相关性和差异性;③很多退化数据都是对固定区域的不同观测对象在一定时间内或者不同条件下进行多次观测得到,这些纵向以及重复性观测数据普遍存在空间和时间上的序列相关性,以往的模型估计方法因未考虑这些相关性而影响了退化模型的准确性。时间序列分析是根据系统观测得到的时间序列数据,通过曲线拟合和参数估计来建立数学模型的理论和方法[13],因此本文采用带有时间序列的混合效应模型描述退化过程。混合效应模型由固定效应和随机效应两部分组成,既可以反映总体的平均变化趋势,又可以提供数据方差、协方差等多种信息来反映个体之间的差异,而且在处理连续观测数据空间和时间上的序列相关性等问题时具有其他模型无法比拟的优势。 在传统回归的基础上添加随机效应,构建如下完整的线性混合效应模型[15-16]: (2) 以本文采用的激光退化数据集为例,通过模型比较后发现,对基础模型进行异方差调节前后不存在统计学差异,而采用自相关调节可显著改善模型,因此只在基础模型的基础上进行自相关调节。最终确定的激光退化(运行电流增长量)和运行时间之间的混合效应模型如式(3)所示,其中:下标m表示误差的方差—协方差矩阵中含有的激光退化集的个数,n表示每个激光退化集观测值的个数。 εi~N(0,Ri); (3) 根据混合效应模型的假设,退化过程中任意观测点退化量的分布均满足正态分布,因此系统从当前退化状态转移到下一退化状态的条件概率也满足正态分布。已知现有系统状态,对下次监测时的退化量所服从的条件概率分布的均值和方差的推导过程如下: 假设从0时刻的初始状态Y0=y0开始检测,通过定期检查的方式进行监测取样,检查间隔为h,当前退化量为 yn=antn+b+εn, (4) 则下一时刻的退化量为 由此可得从当前状态转移到下一状态的条件概率均值和方差分别为: E(yn+1|yn)=h·E(an)+yn; Var(yn+1|yn)=h2·Var(an)+2σ2-2ρ·σ2。 (6) 即给定当前状态退化量yn,下一时刻退化量的条件概率分布满足 yn+1|yn~N(h·E(an)+yn,h2· Var(an)+2σ2-2ρ·σ2), (7) 该分布可用于后期构建基于SMDP模型的状态集并求解状态转移概率矩阵。 求解最优维修策略的方法包括神经网络算法、策略迭代算法、值迭代算法和极限控制算法等,SMDP在求解过程中常采用值迭代法和策略迭代法[17]。策略迭代法考虑系统处在每个状态所采取的维修决策的组合,与系统的运行时间无关;策略迭代算法是求解SMDP的基本方法之一,主要包括“策略评价”和“策略改进”两部分,策略评价是通过线性方程组获得某策略各个状态相应的准则值及其单位期望成本,策略改进是通过迭代不断更新当前策略来产生收敛的决策序列,从而找到最优策略。策略迭代算法的具体实现过程是在初始策略的基础上,根据最优方程求解出每个状态相应的准则值和单位期望成本,然后通过最小化准则值改进策略,并与改进后的准则值作比较,按照该流程反复迭代,直到两次结果相同为止,此时的策略即为最优维修策略。本文采用策略迭代法作为求解算法。 本章对SMDP的模型假设、模型构建、算法实现进行简要阐述,详细论述和推导过程可参见文献[9,17-19]。 模型研究是对实际过程的抽象和简化,本文有如下假设: (1)系统从新造状态向最终失效状态的缓慢退化过程不可逆,假设初始状态为完好状态,失效阈值ω之后为失效状态,则二者之间为系统正常运行状态。 (2)因为退化不可逆(不可修复),所以设置各状态下有更换和不修不换(继续运行)两种可选决策,在执行更换后,系统恢复到新造状态。 (3)随着时间的推移,系统失效风险逐步增大,即运行状态的超限风险增大,系统故障的风险也增大,因此引入失效惩罚成本来表征这一特征。 SMDP模型的构建过程,即为六元组中各元素的确定过程。 2.2.1 状态集 状态集指缓慢退化系统在自然退化过程状态、实施过不同维修后的状态和完全故障状态等所有状态的集合。假设激光器退化过程中电流的最大增长量为4%,激光器发生失效的阈值ω=3.875%,初始状态Y0=y0,以固定间隔Δ将连续状态空间[y0,ω)划分为等区间(将混合效应模型描述的连续性退化过程离散成L个状态),并设定[ω,4)为失效状态,则退化过程的状态数为 L+1=(ω-y0)/Δ+1。 (8) 定义k∈{1,2,…,L+1}为退化量y的离散化状态,其中状态1为新造状态,状态L+1为失效状态,状态2,…,L为系统退化过程状态,因此状态空间可以表示为S={1,2,…,L+1}。若yk表示状态k下的退化量,则 (9) 当监测到系统处于失效状态[ω,4)时,需要立即进行更换。 2.2.2 行动集 行动集与最优决策的选择相关,当系统状态发生变化时,应根据当前时刻的状态做出适当的维修行为。定义A(k)为行动集,a(k)为系统处于状态k时所采取的维修行为,本研究设置更换和不修不换(正常运行)两种维修行为,则a(k)∈{1,2},其中a(k)=1表示不修不换,a(k)=2表示更换。退化过程中每个系统状态的可选行动集不同,行动集 (10) 2.2.3 逗留时间 逗留时间τ(k,a(k))表示系统处于状态k时采取维修行为a(k)后转移到下一个状态的时间的数学期望。假设更换激光器的停机时间和更换时间可忽略不计,检测周期为h,则状态逗留时间为h,具体表示为 (11) 2.2.4 报酬函数 期望报酬函数c(k,a(k))表示系统采取维修行为a∈A时,状态k转移到下一个状态的成本。因为退化量在下一个检测周期内超过失效阈值会增加故障风险,从而导致较高的失效成本,所以本文采用惩罚成本刻画退化过程中超过失效阈值对单位期望成本的影响。若当前检测点的激光退化量yk<ω,下一个检测点的退化量yk+1有一定的概率超过失效阈值,则产生一定的惩罚成本,反之惩罚成本为0。文献中用到的惩罚函数多为指数函数,且与失效概率函数有关[16],因此期望惩罚成本函数可表示为 (12) 式中:c为惩罚系数,f(yt)为失效概率函数。本文的报酬函数包括检测成本Ci、更换成本Cr和惩罚成本Cp,则系统在状态k下选择某一维修行为a(k)的成本为 (13) 2.2.5 状态转移概率 SMDP模型中退化转移过程满足Markov性,即无记忆性,在状态空间S={1,2,…,L+1}时,正常运行和更换状态下的状态转移概率分别做如下定义: (1)正常运行的状态转移概率 (14) (2)更换的状态转移概率 (15) 2.2.6 准则函数 准则函数Vk(Q)为策略Q下状态k的准则值。在策略Q下,每个状态的最优方程为 τ(k,a(k))g(Q)+Vk(Q)=c(k,a(k))+ (16) 本文以单位期望成本最低为优化目标,利用式(16)的优化方程进行反复迭代,最终确定最优维修策略。 本文采用策略迭代算法对SMDP模型进行求解,策略迭代算法的思想为:任意选定一个初始策略,通过引入变量进行下一个具有更低长期预计成本的新策略,如果新策略的成本率比原方案低则继续进行迭代计算,如果新维修策略的成本率与原方案相同则停止迭代,此时的成本率即为最佳成本率,最后得到的策略即为要选择的最佳维修策略。策略迭代算法的流程如图2所示。 具体步骤描述如下: 步骤1设置初始策略R1。策略集R为各个退化状态对应的维修决策集合,Rq={a1,a2,…,aL+1},ak∈A(k),1≤k≤L+1,其中q为迭代次数。 步骤3策略改进。根据步骤2求得的准则值,通过最小化每个状态的准则值Vk(Rq)选择新的策略Rq+1,即用满足式(17)的决策替换原来的决策,从而形成新的维修策略。 g(Rq)τ(k,a(k))]。 (17) 重复步骤2和步骤3并依次迭代,直到Rq+1=Rq时停止迭代,此时的策略R′即为最优策略,同时得到该策略下的单位期望成本g(R′)和各退化状态相应的维修决策。 本文采用Meeker和Escobar提出的GaAs激光缓慢退化系统作为案例[9],以最小化单位时间期望成本为目标,对提出的SMDP模型进行验证和说明。该激光退化数据集包括13个GaAs激光器退化历史数据,数据如图3所示。 在GaAs激光器的使用寿命期内,工作电流的增加由激光器的系统退化引起,当工作电流增加到一定阈值时认为该激光器失效。在该数据组中,每隔20 h测量一次工作电流,直到4 000 h为止。文中使用的激光退化集需要先设定一个需要更换的维修极限值,以制定相对保守的维修策略,从而保证系统在达到故障状态后不会发生安全问题,因此假设激光器退化过程中电流的最大增长量为4%[9],失效阈值为3.875%。 在退化建模阶段,涉及的模型参数包括斜率的固定效应和随机效应系数、截距的固定效应系数、残差方差以及时间序列自相关系数等,利用R语言可以对这些退化模型参数进行参数估计,并将带有一阶自回归(AR(1))调节的混合效应模型与传统线性回归模型和基础线性混合效应模型进行比较。 (1)比较传统线性回归模型和基础混合效应模型,绘制两种模型的残差箱线图,如图4a和图4b所示。 从图4可以看出,传统线性回归模型的残差比较分散,且在0值两侧波动范围较大,而基础混合效应模型的残差集中分布在0值左右,且波动范围较小,说明后者在一定程度上减小了个体层面估计的误差,证明了在存在个体异质性的情况下,混合效应模型优于传统线性回归模型。 (2)在上述比较基础上对带有一阶自回归的混合效应模型与基础线性混合效应模型进行比较,似然比检验指标如表1所示。 选择赤池信息准则(Akaike Information Criterion,AIC)、贝叶斯信息准则(Bayesian Information Criterion,BIC)最小且对数似然函数(Loglik)值最大的模型作为最优模型[16],从表1可以看出本文采用带有一阶自回归调节的线性混合效应模型的AIC和BIC值较小,且其Loglik值较大,似然比检验中P<0.000 1,通过了显著性检验,说明采用带有一阶自回归调节的混合效应模型拟合效果更好。因此,本文采用退化模型的参数估计值更加精确,将其带入式(6),求得已知当前状态时下一状态的条件概率均值和方差,进一步可根据式(14)求解状态转移概率。 本文大部分参数设置与Tang等[9]模型中的参数保持一致,即更换成本为$1 000,检测成本为$1,检查周期为20 h,假设更换时间和停机时间均可忽略。不同的是,惩罚成本通过惩罚函数表示,并设置期望惩罚成本的系数为1.72。固定间隔长度为0.061 5,则最终划分的状态数为64个。另外,从状态转移概率矩阵可以看出,对于每个激光器而言,前59次检查过程中失效的概率不超过0.1,因此在决策过程中设置前59次不进行检测,即首次检查时间为1 180 h。 根据上述分析,维修策略的各参数设置如表2所示。 表1 退化模型比较结果 表2 模型输入参数表 设置初始迭代条件,策略迭代次数q=1,初始策略为 将表2中各参数带入第2.3节的策略迭代算法中,在MATLAB软件下,对基于SMDP的策略迭代算法进行求解,可得激光器的预防性更换控制界限,并得到维修优化模型的求解结果,如图5所示。 从图5可见单位期望成本的变化过程,迭代到第4次时得到维修优化策略,最低单位期望成本为$0.622 94,根据式(9)可得激光器的预防性更换阈值为3.751 5%,即在激光退化过程中,当运行电流增长量达到原始值的3.751 5%时进行更换。 本节将所提基于SMDP的系统维修策略与文献[9]基于役龄的系统维修策略和周期检查模型进行比较分析。传统的基于役龄的维修策略模型采用失效时间的特定分布来计算预先设定执行替换的时间,在退化的全过程中只执行一次检查,并在检查时确定进行预防性维护(Preventive Maintenance,PM)还是纠正维护(Corrective Maintenance,CM)。而周期检查模型是按固定的时间间隔对退化过程进行检测,并设定合理的预防性替换维修阈值,在每次检测后作出适当的维修决策。将3种维修策略应用于激光退化案例(使用相同的激光退化模型参数),比较结果如表3所示。 表3 模型对比结果 续表3 通过表3可以发现,相比于固定周期检查模型,本文所提模型具有相同的检查时间间隔,但是总检查数减少了797次,大大节省了检测成本,而且减少了检测过程对激光器带来的损伤。相比于基于役龄的模型,本文模型具有相同的首次检查时间,但是总体运行时间延长了4 240 h,总成本也有所降低。综上所述,本文基于SMDP的维修决策模型具有一定的成本优势,并且具有较强的可扩展性,更贴近实际的退化过程。 本文考虑退化过程中不同个体的异质性以及重复测量在时间上的相关性等问题,应用线性混合效应模型对缓慢退化系统的退化过程进行建模,在此基础上分析了系统进入各种状态下的状态转换概率,求解了状态转换概率矩阵;针对缓慢退化系统构造了状态空间、行动空间、期望成本和平均逗留时间,设计了基于半Markov决策过程的动态规划模型并进行求解。实例研究结果表明,本文方法可以降低成本率,延长系统使用时间,具有较低的单位时间成本,有助于确定系统更换的极限值,尽早对系统故障做出反应,从而提高系统的安全性和可靠性,降低系统的维修和等待成本。 鉴于本文还存在诸多不足,目前正在进行拓展研究。一方面,研究针对个体的退化规律,将现有的混合效应模型与贝叶斯更新的方法相结合;另一方面,研究针对个体的维修策略优化,考虑建立包括退化时间与退化量的高维Markov决策过程,以适应多维数据特征和个体退化过程,提高预测精度和决策的可靠性。1.2 半Markov决策过程

1.3 退化模型的选择




1.4 最优维修策略求解方法
2 基于SMDP的维修策略模型研究
2.1 SMDP模型基本假设
2.2 SMDP模型构建流程

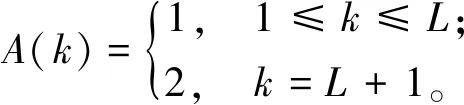
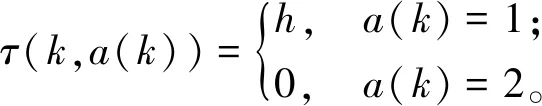





2.3 SMDP模型求解算法的实现


3 实例验证

3.1 模型参数设置



3.2 维修策略优化

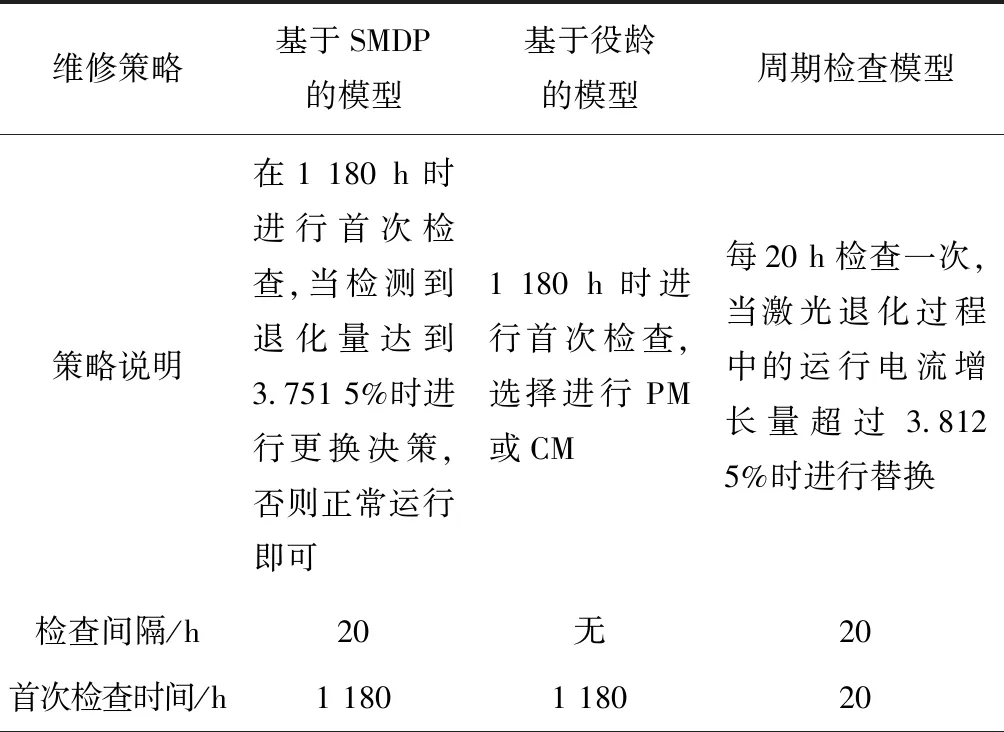
3.3 模型比较

4 结束语
