基于Anusplin秦岭地区近50多年来的降水时空变化

孟 清, 白红英, 郭少壮

(1.西北大学 城市与环境学院, 西安 710127; 2.西北大学 陕西省地表系统与环境承载力重点实验室, 西安 710127)

降水作为最重要的气象要素之一，是气象学、水文学、植被学和生态学等学科领域研究过程中的重要参数之一。而详尽的降水数据、特别是数字化的降水量是支撑多种生态系统模型和径流模拟最主要的设置参数，也是气候变化研究的重要指数，如何获得精度较高的栅格数据成为气候变化研究中的关键问题之一。随着地理学科的发展和GIS技术的进步，空间插值方法应运而生，空间内插就是基于某种数理方法采用已知的气象点数据来推求其未知的气象点数据，从而把矢量数据转换成栅格数据[1]。

常用的气象插值方法有克里金插值法(Kriging)、反距离加权法(Inverse Distance Weighting,IDW)和样条函数法(Spline)等。目前，国内外对气象要素插值方法的研究有很多，关于气温插值通常采用普通克里格方法[2-6]，然而对于降水插值方法的使用一直处于选择阶段，没有一个确定的标准模型。

Daly等[7]对比加勒比海地区的年、月降水以及最高温和最低温插值的结果发现PRISM (Parameter-elevation Regressions on Independent Slopes Model，PRISM)模型的插值效果优于IDW方法。Marquínez等[8]基于多元回归方法和GIS技术手段对西班牙坎塔布连山区降水进行插值分析，结果表明多元回归法能够估计无气象站点地区的降水信息，并且指出地形对降水有主要的影响作用。石朋[9]、刘智勇[10]等都认为协同克里金方法的降水插值效果优于距离平方倒数法和普通克里金法。庄立伟等[11]在对东北逐日降水插值中认为IDW方法要优于克里格方法。王江[12]、谭剑波[13]、蔡福[14]等对比分析了基于Anusplin的薄盘样条法(Thin Plate Spline，TPS)与传统插值方法对降水数据进行插值比较，结果都一致认为TPS法对基本气象要素的插值误差最小。姜晓剑[15]、刘志红[16]、钱永兰[17]等针对基于薄盘样条法的Anusplin降水插值，分析了TPS的误差和应用。

由于前人研究结果具有可靠性，但是不同的研究人员选取的研究方法不同，研究区域存在地形差异及数据时间尺度和空间尺度来源不一致，所得降水插值的精度误差也不同。就目前降水插值的研究方法来说，普通克里金方法很少考虑地形因素的影响；PRISM适宜于地形起伏较大的地方；多元回归分析的优点在于估算的降水量不依赖于估算点周围区域气象站点的密集程度，可以直接根据地形参数求出降水量；而基于Anusplin的薄盘样条法是一种采用平面平滑样条函数对多变量数据进行分析和插值的工具，它不仅考虑了地形对降雨量的影响，而且考虑了气象站点分布及数量对降水插值的影响，且有研究表明Anusplin对降水的插值结果优于其他几种插值方法[18-21]。

秦岭山地作为中国南北分界线，北仰南俯，相对高差大、最高海拔为3 771.2 m，由于长期缺乏高山气象站点，导致秦岭山地栅格降雨量数据难以获取。同时秦岭地区的降雨量对于全国的水热平衡、植被生长和农作物的产量等具有重要的影响作用。因此本文基于Anusplin软件以秦岭山地为研究对象，以DEM数据和31个气象站点1959—2015年的降水数据为基础，评估Anusplin插值方法在秦岭山地的适用性，阐明秦岭地区56年来降雨量的时空分布特征和变化趋势，旨在为探索全球变化和局地小气候的相关研究提供科学依据和理论支撑。

1 研究区概况

本文所选区域为秦岭腹地(图1)，俗称“小秦岭”，位于东经103°48′—113°04′，北纬32°25′—35°16′。秦岭是中国南北分界线，是1月0℃等温线、800 mm等降水量线以及北亚热带和暖温带的分界线，同时还是长江水系和黄河水系的分水岭等[22]。秦岭山地具有北仰南俯的特征，分布着海拔2 500 m以上的中山和3 000 m以上的高山[23]，最高海拔为太白山的拔仙台，海拔3 771.2 m。秦岭地区年均降水量600～1 200 mm，汛期6—9月的降水量占全年的60%左右，降水变率大，季节分配不均匀[24]。由于秦岭山体庞大，冬季能阻挡寒冷的西伯利亚寒流南下，使南方减少冻害；夏季又可以阻挡太平洋上湿润的水汽北上，使得中国南北出现了不同的气候类型和植被类型[25]。

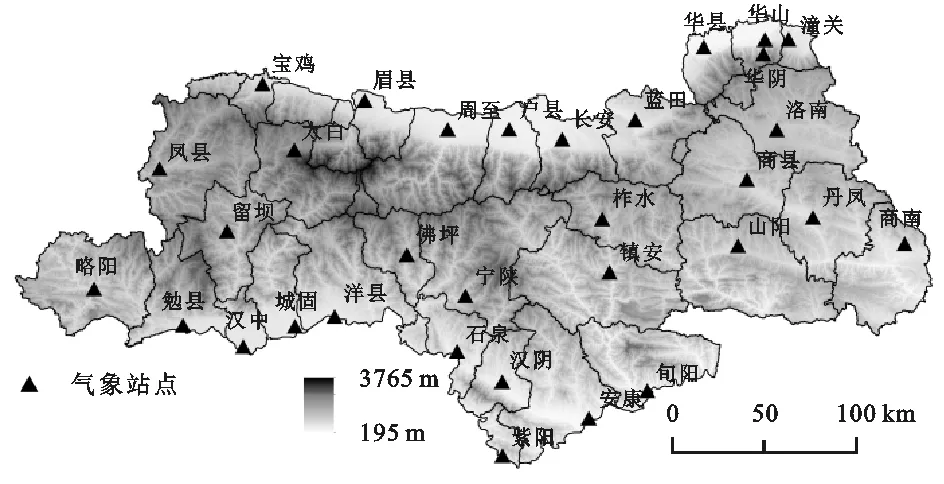
图1 研究区及气象站点分布

2 研究方法与数据来源

2.1 Anusplin插值方法

Anusplin是一种采用平面平滑样条函数对多变量数据进行分析和插值的工具，它最早是由澳大利亚学者Hutchinson在总结前人经验基础上研发的。Anusplin是基于普通薄盘和局部薄盘样条函数插值理论。局部薄盘光滑样条是对薄盘光滑样条原型的扩展，它除通常的样条自变量外，允许引入线性协变量子模型，如温度和海拔之间、蒸发量与水汽压差的相关关系。

局部薄盘光滑样条的理论模型表述如下：

zi=f(xi)+bTyi+ei(i=1，…，N)

(1)

式中：zi为位于空间i点的因变量；xi为d维样条独立变量；f为要估算的关于xi未知光滑函数；yi为p维独立协变量；b为yi的p维系数；ei为具有期望值为0的自变量随机误差。

当公式(1)中缺少第2项，即协变量(p=0)时，模型简化为普通薄盘光滑样条；当缺少第1项独立自变量时，模型变为多元线性回归(Anusplin中不允许这种情况出现)[26]。本文在对降水进行插值时，使用三变量局部薄盘光滑样条函数(经度和纬度为自变量，海拔高度为协变量)，样条次数设置为2。

2.2 一元线性回归分析法

此方法可以对降水栅格图中的每个像元的变化趋势进行模拟，采用最小二乘法计算其倾向值，用来估计时间序列与降水序列的回归系数[27]。

2.3 误差分析

分别使用2013—2015年位于南坡的城固、丹凤、位于北坡的华阴3个未参与插值的低海拔样点和红河谷、太洋公路2个中、高海拔样点来检验误差，通过根均方差(root mean square error, RMSE)和平均绝对误差(mean absolute error, MAE)2个指标来评估秦岭地区降水插值的效果，通过3 a标准差来评估秦岭地区降水插值误差的稳定性。

(2)

(3)

2.4 数据来源及预处理

本文所研究的降水数据来源于陕西气象局1959—2015年12个月数据，31个气象站点，其中秦岭南坡22个、北坡9个，气象站点如图1所示。剔除不连续、冗余及错误的数据，对数据进行一致性检验。对原始数据进行标准偏度系数分析，当偏度系数>0时，表示降水变化更趋向正值，呈正偏态分布；当偏度系数=0时，呈正态分布；当<0时，表示降水变化呈负偏态分布[28-29]。正态性检验的方法有多种，W检验(Shapiro-Wilk检验)适合于小样本(n≤10)，本文采用Kolmogorov-Smirnov检验法。检验结果表明秦岭山地1959—2015年年降水量数据符合正态分布(p>0.05)(表1)，所以对原降水数据无需进行变换。

表1 降水偏系数检验结果

DEM数据分辨率为25 m×25 m，数据来源于陕西省测绘地理信息局，本文以此为基础根据研究需要，重采样分辨率为500 m×500 m。

3 结果与分析

3.1 多年年均降水栅格空间分布特征

依据Anusplin方法，得到了秦岭地区1959—2015年57 a的年、季均降水栅格空间分布(图2)，其栅格分辨率为500 m×500 m。经对图2空间分析可知，秦岭地区57 a多年年平均降水的范围为545.44～1 155.46 mm，平均降雨量为824.76 mm，空间分布总体呈现南丰北少的分布，其中西南部降水较多。南坡57 a年均降水的变化范围为601.97～1 155.46 mm，平均降雨量为847.37 mm；而北坡降水变化范围为545.44～1 061.84 mm，平均降雨量为737.25 mm，即南坡降水明显多于北坡110.12 mm左右。秦岭山地四季平均降水量大小依次为：夏(403.76 mm)>秋(237.26 mm)>春(169.11 mm)>冬(25.62 mm)，且南坡降水大于北坡降水。以往的研究表明[30]，秦岭山地是800 mm分界线，北坡年均降雨量小于800 mm，南坡大于800 mm，本文所获得的降雨量与前人的研究结果基本一致。但经过对图2像元统计分析后发现，南坡亦有降雨量小于800 mm的像元数53 051个，占总像元的29.34%，主要分布在洛南和商州区等地区；北坡降雨量大于800 mm的像元数有14 106个，占总像元的29.7%，分布在长安、户县和周至的南部地区。虽然获得的栅格数据比实测点数据更能全面地反映秦岭地区多年降水的空间分布，但其精度还需进一步的检验。

3.2 降水栅格数据集的误差检验

3.2.1 系统自检验 图3为系统输出误差图，从图中可以看出，误差范围为0.01～0.03 mm，表明系统自检验合格，但误差与海拔密切相关,如秦岭主峰太白山的误差最大，为检验获取的栅格降水数据集的准确性与科学性，本文进一步用实测样本来进行误差检验。

3.2.2 实测样本检验

项目划分是施工质量评定的框架。目前，工程施工质量项目划分存在不少问题，不利于有效地实施工程施工质量管理。例如：工程项目未按程序进行划分和申报，甚至个别工程项目由施工单位提出划分意见后，未报监理单位、建设单位、质量监督机构确认，造成了划分不当、无法进行质量评定等状况；项目划分中单元、分部、单位工程名称与施工合同、设计文件中的名称不一致，造成检测、评定资料和总结报告中出现一个项目多个名称现象；工程未按项目划分进行质量检测、评定和资料存放，项目划分与资料整编不统一，甚至出现一个分部工程中含有另一个分部工程的单元工程，使质量评定无法进行。

(1) 中低海拔样点误差检验。由于秦岭气象站点大多数分布在400～1 000 m的中低海拔地区，为了进一步检验插值的准确性，应用2013—2015年3个未参加插值的观测站点(位于南坡的城固、丹凤和位于北坡的华阴)为样点，与栅格图对应样点进行误差分析。误差通过RMSE和MAE来表示,表2显示了二者之间的月误差，结果表明，处于夏秋季节误差大于春冬误差，出现这一现象的原因可能是秦岭地区夏秋季节雨水充沛且多暴雨，不确定较多，冬春寒冷而干燥、降雨量有限。由标准差结果可知(表3)，3 a来华阴县降水最为稳定，丹凤县最不稳定；降水标准差基本在20 mm以内。

图2 1959-2015年秦岭地区年、季均降水量空间分布

图3 1959-2015年秦岭地区年均降水量预测误差

(2) 高山样点误差检验。长期时间内，由于秦岭高山站点稀缺，无站点观测资料，但另一方面秦岭由于山体高大，地理环境复杂，林线区对气候变化响应敏感，本文为了进一步验证秦岭地区降水插值精度，选取未参加插值的太白山2个中高海拔样点(红河谷和太洋公路)仅有的近3 a的气象资料来进行验证。由表4可知，处于夏秋季节的误差大于春冬误差，这一结果与低海拔误差检验的结论一致。降水标准差范围基本在30 mm内。

通过自检验、中低样点误差检验和高山样点误差检验，表明误差在范围内，栅格数据集比较科学。

3.3 基于降水数据的3种插值方法的比较

为进一步说明Anusplin的插值精度，选取气象学常用的两种插值方法进行横向对比分析，两种插值方法分别是普通克里金插值法(Ordinary Kriging,OK)和反距离加权法(Inverse Distance Weighted,IDW)，对秦岭山地57 a年均降水量进行空间插值，如图4所示，再分别对3种插值结果的29个站点实测值和插值进行相关分析，结果发现，基于普通克里金、反距离加权法和Anusplin插值法的降水结果精度具有差异性(图5)。Anusplin的精度最优，相关性为0.99；其他两种方法的相关性均为0.91。由图4可知，基于3种插值方法的秦岭山地57 a年均降水均呈南丰北少。陕南的安康和汉中因受纬度、地形和海拔，降水量呈高值，而秦岭北麓及东部商洛地区降水较少。Anusplin方法在空间分布上明显比其他两种方法平滑，更清晰地表达出秦岭山区降水的分布状况，而其他两种方法的插值结果均出现了“牛眼”。由此可见，Anusplin插值法更适合秦岭地区的降水插值。

表2 中低样点2013-2015年各月值误差对比

表3 中低样点2013-2015年降水插值结果与实测结果的标准差对比

3.4 1959-2015年秦岭地区降水变化特征

由一元线性回归方法经过ArcGIS 10.3处理，获得了秦岭地区57 a的年、季均降水量变化率分布(图6)。1959—2015年秦岭地区年均降水变化率在-3.02～0.83 mm/10 a范围内，秦岭地区东部商洛地区变化率最大，达到0.83 mm/10 a；降水变化呈上升趋势的地区在秦岭南坡的略阳、石泉和商南等地区，平均海拔分布在811 m；降水变化大部分呈下降趋势的地区在秦岭主峰太白山和秦岭南坡安康等地区，平均海拔分布在1 177 m。春夏秋和冬季变化率分别在-0.73～0.65 mm，-2.73～2.50 mm，-2.13～3.69 mm和-0.20～1.02 mm，在57 a尺度上，增加和降低趋势均未通过显著性检验。

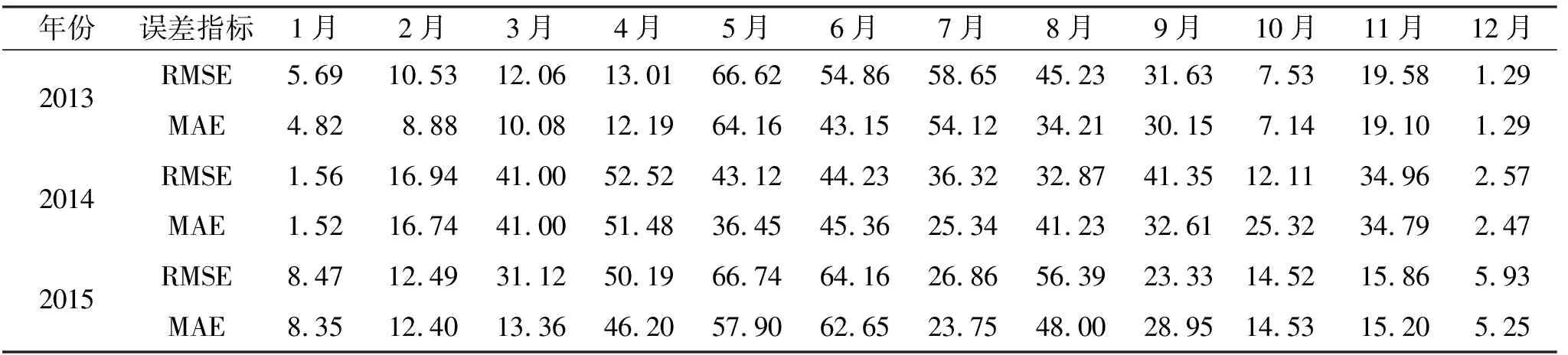
表4 高山样点2013-2015年各月值误差对比

表5 高海拔样点2013-2015年降水插值结果与实测数据的标准差对比

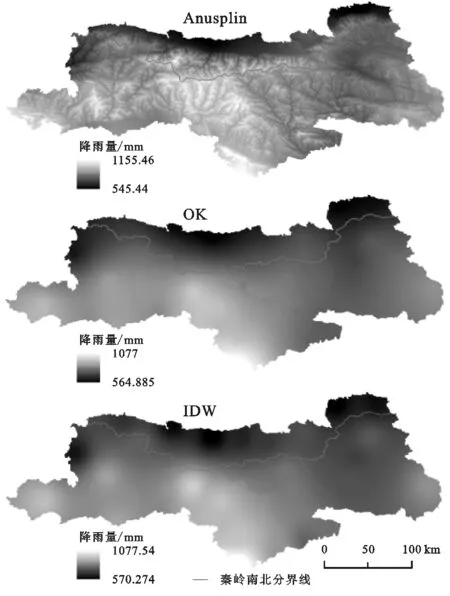
图4 基于不同插值方法的秦岭地区57 a年均降水量的空间分布

图5 基于不同插值方法的秦岭地区57 a年均降水量实测和插值散点图

图6 1959-2015年秦岭地区年、季均降水量变化率的空间分布

4 讨论与结论

4.1 讨 论

(1) 本文基于Anusplin软件得到了秦岭地区1959—2015年的月降水栅格信息和年降水栅格信息，为一些径流模型和生态模型提供了数据基础；目前，针对降水插值没有一个完全合适的方法，而澳大利亚气象软件Anusplin是一个目前较为适合的方法，但是对于某些高山地区气象因子的插值还存在精度较大的问题，未来的发展方向就是继续寻求一个精度小、融合多因子、适合不同种类地形的插值模型。

(3) 而本文进行插值是基于31个气象站点，由前人所得结果可知，增加气象站点的数量可提高插值的精度，所以误差存在的一部分原因在于秦岭地区气象站点的有限性；中、高海拔误差普遍较低海拔误差大且不稳定，如何减小误差、改进方法未来还有待提高。

4.2 结 论

(1) 获得了数字化降水栅格图。结果表明，近57年来，秦岭地区平均年降水的变化范围为545.44～1 155.46 mm，空间分布总体呈现南丰北少的态势，其中西南部偏高。秦岭地区年均降水量存在南北差异,南坡57 a降水的变化范围为601.97～1 155.46 mm，平均降雨量为847.37 mm；而北坡降水变化范围为545.44～1 061.84 mm，平均降雨量为737.25 mm；南坡年均降水多于北坡110.12 mm；秦岭山地四季平均降水量大小依次为：夏(403.76 mm)>秋(237.26 mm)>春(169.11 mm)>冬(25.62 mm)，且南坡降水大于北坡降水。

(2) 中低海拔样点检验结果表明，处于夏秋季节的误差大于春冬误差；3年来华阴县降水最为稳定，丹凤县最不稳定；降水误差基本在20 mm以内。相比较低海拔样点的误差，高海拔的夏秋季节误差大于春冬误差；降水标准差范围基本在30 mm内。基于Anusplin方法的实测值与插值结果拟合较好，相关性达0.99。

(3) 1959—2015年秦岭地区年均降水变化率的范围为-3.02～0.83 mm/10 a(均未通过显著性检验)，高海拔区域降水呈减少趋势，中低海拔地区降水在增加；秦岭地区东部商洛地区变化率最大，达到0.83 mm/10 a；降水变化呈上升趋势的地区在秦岭南坡的略阳、石泉和商南等地区，平均海拔分布在811 m；降水下降区为秦岭主峰太白山和秦岭南坡安康等地，平均海拔分布在1 177 m。