巧置问题情境 激发学生思考——《万以内数的大小比较》教学实践与思考

江苏省海安市城南实验小学 刘智勇

教材分析

《万以内数的大小比较》是二年级《数学》下册《认识万以内的数》这一单元例8的教学内容，教材中给了4种电器的价格，要求比较电视机和空调的价格以及电视机和电冰箱的价格。

教材精心选择四种电器单价的数据：有四位数，也有三位数；四位数中最高位上的数有不相同的，也有相同的。这的确为学生探索比较数的大小的方法提供了丰富的素材。在以往的实际教学中，学生不能领会教材编写者的良苦用心，教师按教材的编排进行教学，教学过程平淡如水，学生的学习热情也不高。是学习素材不吸引学生，还是知识本身缺乏吸引学生的因素呢？在新一轮的教学前，我决定进行一次学前调查。

两次调查

我设计了如下的题目，在学习这一课之前进行了一次小调查。

在○里填上“＞”“＜”或“＝”。

357○458 9330○8740 786○783 9362○9370

1000○999 588○5880 3□□○4□□ 8□□○8□□□

你觉得哪几道题最容易比较大小？为什么？

学生完成后，我对学生的作业进行了统计，前6题中，62名学生中只有两名学生有错，后面两题中，除了个别学生没能弄清题目的意思导致出错外，大部分孩子的作业全对。看来经过前面数的读写与组成的学习，以及一年级百以内数的大小比较的学习，学生已经能够顺利地将数的大小比较的经验和方法进行迁移学习和使用。对于哪几道题最容易比较大小，62名学生中有39名学生认为1000○999和588○5880最容易比较。学生的判断理由有的直接聚焦到一个是四位数，一个是三位数，四位数大；有的则从整体上作出了归纳：比较位数就可以了。

二年级的学生学习这一知识，前面铺垫的东西太多，一年级的学生对这个知识又会作出怎样的解答呢？我又到一年级对部分学生进行了调查。经过调查，我发现一年级的孩子虽然没有能正确读出万以内的数，但他们对于数的大小比较的判断却都是正确的。

两次的调查可以看出，比较数的大小对于学生来说并不是特别困难的事，所以用纯数学的眼光来进行这一内容的教学，学生难免会失去学习的兴趣，缺少一份学习的动力。基于以上的调查和分析，我决定对《万以内数的大小比较》进行一点小小的探索与尝试。

课堂实践

针对以往教学中出现的问题，我设置了如下的情境和问题：

问题一：老师准备买一款洗衣机，我跑了两家大商场（出示：价格），你建议我到哪家商场买？为什么？

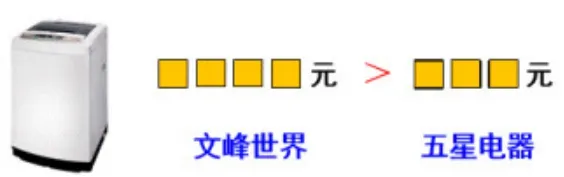
学生交流后追问：图中都没有出现具体的数字，你们怎么能看出五星电器的便宜的呢？

小结：不同位数的数比较大小，位数多的数大，位数少的数小。

问题二：老师打开支付宝一看（出示图一），请问可以买到这台洗衣机吗？为什么？

图一

图二

追问：在什么情况下可以买得到，什么情况下买不到呢？

在学生交流的过程中，逐步出示价格牌中某一位上的数字，引导学生思考钱够还是不够。

小结提问：刚才我们讨论能不能买到这台洗衣机，其实就是在比较两个数的大小。结合刚才的讨论，想一想，我们怎么比较两个数的大小的？

学生讨论，在讨论的基础上得出：比较两个数的大小，首先比较两个数的位数，位数多的数大，位数少的数就小；位数相同的时候就先比最高位数，最高位上的数相同就再比下一位……

问题三：老师的微信钱包里也有零钱（出示图二），现在能够买到这台洗衣机吗？为什么学生又一次进行思考和争论，在学生又一次进行思考和争论，在思辨的过程中再一次巩固数的大小比较的方法。

问题四：请你来当小老师，出几道数的大小比较的题考考同桌，出完题后在另一页纸上写下你的标准答案。

学生出题，互相解答，课后思考。

在本课的教学中，我没有出示完整的数让学生比较，而是通过在不同的问题情境中出示一个个不完整的数去激发学生思考，引导学生关注比的重点，从而掌握数的大小比较的方法。

一、参谋到哪儿买，领会数的比较第一招

课前的调查显示，三位数与四位数的比较是学生认为最容易进行的，教材中把它放在学生的交流中进行，无疑丢失了一个给所有学生发现这一知识的机会，但是如果只是干巴巴地呈现一个三位数和一个四位数，也难激发学生的学习兴趣。因此这里问题的呈现要让学生关注到数的位数，而忽略每一位上具体数，才能让学生领会到比较两个数，先看位数。显然，问题中两位被挡住数字的价格牌燃起了学生思维的火花，他们的生活经验和数学经验帮助他们做出了合理地选择与解释。这与平时模样不同的问题吸引了学生的兴趣，激起了学生思考的欲望，也让学生轻松掌握了数的大小比较的第一招：比位数。

二、判断够不够买，理清数的比较方法

学生掌握了数的大小比较的第一种类型后，我仍然没有出示完整两个三位数去让学生比较它们的大小，而是出示了支付宝里的钱，让学生判断我的钱够不够买这台洗衣机。在学生交流的过程中，我结合学生的发言进行了板书。板书中有的是具体的数字，也有的是用方框代替数，这样的目的是为了让学生知道在比较相同位数的数的大小时，我们要注意的是关键数位上的数，比如最高位上的数的不同，那只要看最高位上的数，后面的数位上是多少就不重要了，方框代替数正好完美地达到了这一目的。经过一次次交流与辩论，学生理解并掌握了比较数的大小比较的方法。在整个学习过程中，学生的思维很活跃，他们积极参与到问题的探究中，对够不够买进行判断，同时要能够正确判断别人的意见，在与同学的对话与交流中，不断完善自己的思考，从而积累知识经验，最终形成自己的完整的数的大小比较的方法。

三、出题考考同学，巩固数的比较方法

知识掌握得如何，要看用得怎么样。但单纯的解题练习会给刚刚一头激情的孩子泼下一盆冷水，如何让他们保持这份激情呢？一番思考，我决定给他们一次出题的机会：出几道题考考你的同桌。学生出的题有的很常规，但也有些有陷阱，甚至有些题把自己也陷进去了。有名学生出了这样的题：□4□□○□□4□，也许这名同学自己在出题的时候只注意到了4所在的位置，因此给的“标准答案”是＞，而这道题，其他同学给出了不同的答案。究竟谁对谁错，学生又展开了一次讨论，对于数的大小比较的方法又有了新的认识。

我们常说要让学生跳一跳摘到桃子。我想，这其中的关键不是怎么摘桃子，而是把桃子放在什么地方，只有当桃子的位置放得合适，学生才会有跳的欲望，也才会有跳的激情，他们才会主动去思考如何摘桃子。在教学中，我们要多创设一些能让学生跳起来的问题情境，真正点燃学生思维，让学习在不断的思考中行进，在行进中收获方法，让学生真正充满活力。