矩形巷道围岩应力分布规律与粘弹性变形分析研究

韩涛

（山西省长治经坊煤业有限公司山西长治047100）

0 引言

运用理论分析的手段，根据弹塑性力学机理推导出矩形巷道围岩应力应变之间的函数表达式，通过公式可以更加直观的反映出不同因素对矩形巷道围岩应力应变的影响关系，再结合相关的相似模拟以及数值模拟对其进行校核、修正、完善。因此，较为成熟的理论分析手段对于实际工程生产越来越显得尤为重要。本文采用复变函数理论分析方法解决了应力计算不连续的相关问题，并可在一定程度上减少计算繁琐的问题，对实际工程中巷道围岩稳定性的判断具有一定的指导作用，并为巷道支护方案的设计提供参考。

1 工程概况

3-8051 顺槽煤层倾角2°～6°，长1 157.91 m，煤层平均厚度6.3 m，直接顶是泥岩，厚约1.28 m，基本顶是砂质泥岩，厚约6.83 m，直接底为泥岩，厚约0.57 m，基本底为细粒砂岩，厚约2.93 m。

3-8051顺槽设计长度为1 157.91 m，矩形断面，净宽为5.2 m，净高为3.1 m，沿3#煤层底板掘进。

2 理论分析

2.1 矩形巷道围岩应力分析

2.1.1 力学模型建立

矩形巷道围岩周围应力在巷道开挖及采掘过程中进行重新分布，影响应力重新分布结果的因素有：地质条件、巷道围岩特征以及围岩的岩石力学性质等。为了更好的研究矩形巷道围岩应力分布特征，建立了力学分析模型（图1）。对矩形巷道围岩应力的分析按照平面应变问题来进行处理，模型边界按照5 倍巷道面积大小来进行设定，该模型也同时符合了弹性力学中关于忽略自重、均值、弹性、各项同性及小变形等相关假说。

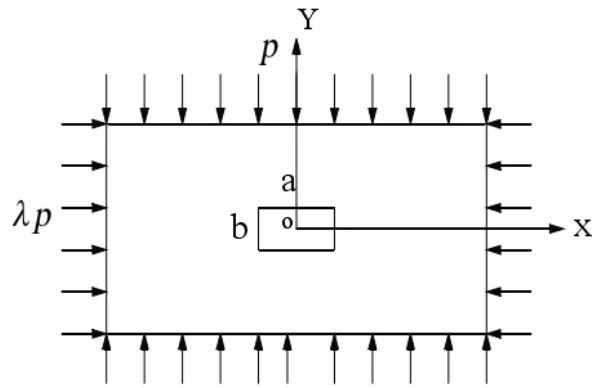
图1 矩形巷道原岩应力场分布模型

2.1.2 保角映射与曲线坐标

煤炭洗选加工要形成比较合理的结构和布局。原煤入洗比重达到70%以上。原则上不销售和使用毛煤。建成一批不同规模、不同品种、不同用途的现代化煤炭洗选加工基地。技术装备、工艺流程、全员工效和自动化程度接近国际先进水平，进入世界煤炭洗选加工强国行列。

通过在弹性介质边界上确立已知条件，利用所得复变函数关系式，可以得出具体的保角转换复变函数，以此可以进一步得出矩形巷道应力具体的函数表达式，这里所用的保角转换函数z的关系式为[1-2]：

通过对矩形巷道进行理想化，视为理想弹性体状态，把矩形巷道围岩断面（XZ平面）上的面积矢量转换成L 平面域上来，可得在L 平面域上l=ρ( cos θ+i sin θ )=ρeiθ，则通过极坐标表示L 点的形式为（ρ,θ），在L 平面上ρ、θ 的圆周参数均为恒值常数。据此，ρ、θ 可以被看成在XZ 平面上的一点曲线坐标，其中i为保角系数，一般取1.2。具体转换关系示意图如图2所示。

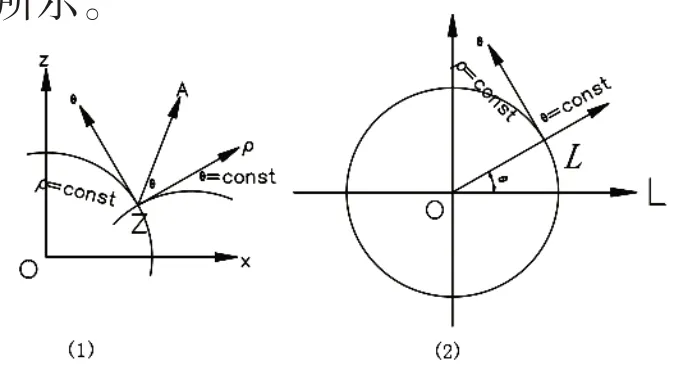
图2 极坐标转换示意

通过上述的转换原理及方法，可将矩形巷道平面问题转换成单位圆平面问题。这样可在计算过程及计量上使矩形巷道围岩应力的求解变得简单很多，通过转化所得的解析函数φ( l ),φ( l )可以用来表示矩形巷道围岩的应力及位移。表达式如下（公式一）：

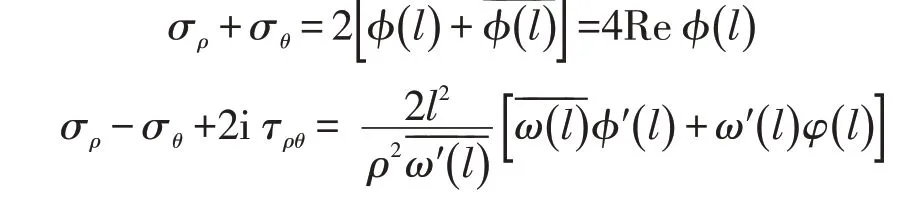
与之相关的关系表达式还有公式2：

式中：FX、FY分别对应X、Y 方向上的面力之和。φ0( l ), φ0( l )分别表示在单位圆L 内的复势函数，并且在单位圆范围内（涵盖圆周的外边界）具有连续性。B，B′，C′是表示在原岩应力场中σρ,σθ有关物理量相关的常量，可表示为（公式3）：

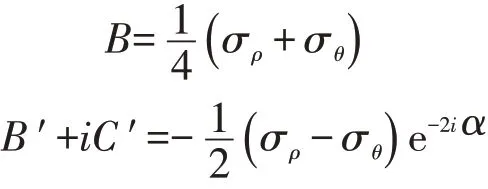
式中：α 为原岩应力主应力方向。

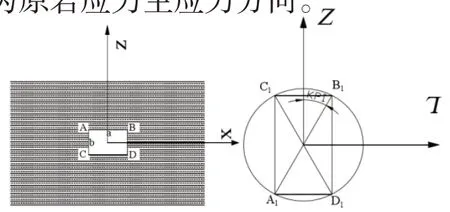
图3 矩形巷道平面与单位圆平面映射关系

如图3，其中任何一点在L关系平面内都可以表示为l= ρeiθ的形式。

2.2 矩形巷道围岩粘弹性变形特征分析

因巷道本身具有非常显著的流变特性，所以在采掘过程中以及掘进完成后，巷道围岩容易出现裂隙和弹性变形等围岩不稳定现象。巷道在刚开挖后，原岩应力状态被破坏，巷道岩体本身表现为弹性状态，随着时间的增加，开挖后的巷道围岩出现稳定且缓慢的蠕变特性，在这个动态的过程中，巷道围岩同样出现应力松弛现象，依据以上的分析以及根据岩石的流变特性，我们可以选用Poyting-Thomson（鲍尔丁-汤姆逊）模型[3]以及广义的达尔文模型来进行彼此之间的对比分析。

2.2.1 poyting-thomson模型

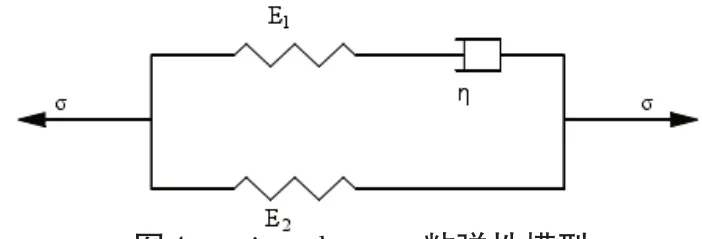
图4 poyting-thomson粘弹性模型

该模型的本构方程为（公式4）：

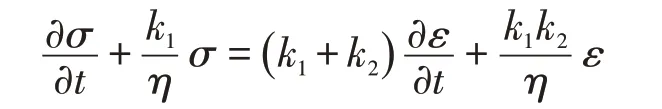
在具体分析问题时，抓主要因素，忽略掉次要因素，使问题简易化，可将巷道围岩的体积变形看成弹性变形，依据相关的机理及理论对问题进行定性分析。poyting-thomson模型的本构方程表示为偏张量形式的表达式为（公式5）：

由上式的关系推导可以看出矩形巷道围岩粘弹性的胡克本构关系模型以及求解关系的本构模型与弹性体基本机理性质基本相同，根据实际问题，代入相关变量，即可求出矩形巷道围岩的粘弹性值。

2.2.2 广义达尔文模型

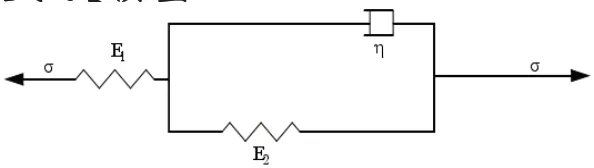
图5 广义达尔文本构模型

其本构关系方程为：trelσ+σ=trelE1σ+E2ε

式中：σ 为矩形巷道围岩应力变量；ε 为矩形巷道围岩应变变量；trel为矩形巷道围岩蠕变应力松弛时间。

利用D 代表时间的微分算数形式，则此模型的本构关系方程可表示为：

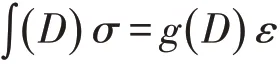
由上式推导关系可以得到矩形巷道围岩的应力应变以及应力松弛时间的求解方法，根据实际问题，代入相关变量，即可求出矩形巷道围岩各个变量的相关值。

3 实际工程应用分析

为对矩形巷道围岩应力理论求解的进一步研究，结合实际工程情况，对矩形巷道围岩应力求解过程进行具体分析。由于本文理论部分研究主要是对矩形巷道与圆形巷道转换分析理论的补充，所以所得公式不足以进行具体的工程应用分析，需引除本文所得公式外，其他的基本推导公式，具体参考文献[1-2]内所示。

3-8051 回风顺槽矩形断面参数为宽5.2 m、高3.1 m。3-8051回风顺槽为全煤巷，其中3号煤的应力松弛时间为4d，瞬时剪切模量为G0=600 MPa，将上述参量带入文献1内对应公式可得：

k=0.164；r=3.96；c1=0.515；c2=-0.123；c3=-0.006；c4=-0.004

结合图1 矩形巷道原岩应力场分布模型可知：X=Y=0，且3号煤埋深400 m，原岩应力q=10 MPa，应力集中系数λ 取1.5，l根据平映射关系，得出值约为1，带入映射函数z=w(l)，以及公式1，公式2 最终得出代入上式可得矩形巷道围岩应力集中处φ( l )=17.8 MPa；=0.3 m。

4 结论

结合工程实际对矩形巷道平面问题转换成单位圆平面问题进行了进一步探讨，可以看出，通过所得公式及所引公式变量之间的关系推导，得出了矩形巷道围岩应力的具体求导公式，并根据实际情况，代入具体参数得出了巷道围岩应力应变值。