融合模糊推理和流形正则化的特征迁移学习*

宋仪轩，邓赵红，秦 斌

江南大学 数字媒体学院，江苏 无锡214122

1 引言

在传统机器学习的分类任务中，为了得到具有高准确性和高可靠性的模型，学习任务往往需要满足以下两个条件：首先是用于训练分类模型的训练样本与测试样本满足独立同分布的条件；其次是存在足够数量的有标签训练样本。而在实际问题中这两个条件往往无法同时得到满足，迁移学习作为一种有效的技术能够有效地缓解上述问题[1]。

迁移学习是运用已有的知识对不同但相关领域问题进行建模的一种有效的机器学习方法[2-4]。它可以将已有的知识进行迁移，用来解决目标领域中仅有少量甚至没有标签样本的学习问题。在实际生活中，随着时间的变化，原先有标签的样本数据可能变得不可用，而且有可能与新的测试样本的分布产生语义、分布上的差异。例如，银行或者金融类的行业的数据就是具有时效性的特点，利用过去的一些金融信息训练出来的模型往往很难准确预测出下一段时间的相关结果。又比如股票、投资等领域，存在很大的不确定性和短暂的信息时效性。除此之外，因为有标签样本数据往往较为稀少，而且很难获得，导致实际生活中没有足够多的有标签数据来训练模型。如果大批量投入人力来标注样本，会导致成本在时间和人力上大幅度增加。另外，由于人的主观因素，被标注样本不一定正确，这就导致了一个问题：人们如何根据已有的少量的数据来训练一个稳定可靠的模型。

为了应对上述挑战，已经有大量文献从不同角度进行了迁移学习策略的研究。常用的三种迁移策略分别是基于特征选择的方法、基于特征映射的方法和基于权重的方法。

（1）基于特征选择的方法是利用源域与目标域中相同的特征进行知识迁移。Dai 等人[5]提出了一种基于联合聚类（co-clustering）的预测领域外文档的分类方法CoCC（co-clustering based classification）。该方法通过对类别和特征进行同步聚类，实现了知识与类别标签的迁移。

（2）基于特征映射的方法是把数据从本来的特征空间映射到新特征空间，使得新特征空间下源域数据与目标域数据分布接近，然后利用新特征空间全新的源域有标记数据进行训练。Matasci 等人采用半监督传递和目标域分量分析[6]，利用最大均值差异[7-8]作为学习新特征空间的迁移策略。Shao 等人[9]讨论一种迁移学习方法用于视觉分类。Yeh 等人[10]提出一种新的领域适应性方法以解决跨领域模式识别问题，并提出核典型相关分析方法（kernel canonical correlation analysis）以处理非线性相关子空间的情况。

（3）基于权重的方法就是根据训练样本对目标领域分类有利程度来给有标签数据添加相应权重，即对训练目标模型有利的训练样本加大权重，否则权重被削弱。Jiang 等人[11]提出了一种实例权重框架来解决自然语言处理任务下的领域适应问题。

在这三种方法之中，基于特征映射的方法由于具有较好的迁移能力而受到了广泛的研究。Pan 等人[8]提出了一种名为传递分量分析,即TCA（transfer component analysis）的域不变特征学习算法，它是将两个域之间的边缘MMD（maximum mean discrepancy）距离的特征表示最小化。TSL（transfer subspace learning）[12]则是采用Bregman 散度而不是MMD 作为比较分布的距离。JDA（joint distribution adaptation）[13]是基于同时减少边缘MMD 和条件MMD 的距离来减小域之间差异。TJM（transfer joint matching）[14]则是通过联合特征匹配和重新加权的方式来减少域之间的差异。而在GFK（geodesic flow kernel）[15]中，子空间维度应足够小，以确保不同的子空间沿着测地线流动平滑，但是这可能无法准确地表示输入数据。虽然基于特征映射的方法已经取得了一些令人满意的效果，但是这些方法往往有如下不足：其一是线性特征迁移方法的迁移能力比较有限，部分算法无法应对非线性场景；其二是现有的非线性特征迁移技术，几乎都是采用核技巧进行非线性特征迁移，缺少良好的可解释性。

针对上述不足，本文探讨了基于模糊推理系统的具有较好解释性的特征迁移方法。模糊集理论和模糊系统作为智能计算领域重要的研究分支，已经应用于各种领域[16-21]。研究表明，模糊系统具有高度的可解释性和强大的学习能力[22]，现已广泛应用于工业过程控制、财务预测、图像处理、医疗诊断等领域[23-24]。

基于模糊推理系统，本文提出了基于不确定推理规则的特征迁移方法FIMR-FTL（fuzzy inference and manifold regularization based feature transfer learning）。FIMR-FTL 利用TSK 模糊系统解决了传统非线性特征迁移方法缺少可解释性的问题，其利用可解释的TSK 模糊系统取代非线性核方法，使得特征迁移的过程具有良好的可解释性。同时，FIMR-FTL还引入了最大均值差异用作分布差异性度量。并且将边际分布MMD 和条件分布MMD 相结合，减少源域和目标域的分布差异。为了达到迁移过程中保留数据有效信息之目的，FIMR-FTL 还在优化目标中引入了数据分布的流形正则化项，从而保证特征迁移前后的数据流形保持稳定。本文所讨论的都是源域和目标域在边缘和条件分布方面不同，并且目标域没有标记数据的场景。

2 相关工作

2.1 特征迁移和领域自适应

在无监督领域适应问题中，数据源来自两个不同的域：源域S和目标域T。从源域中采集有标记数据及其标签，从目标域中采集无标签数据nS和nT是源域和目标域样本个数。

假设源域样本和目标域样本属于相同的特征空间。令PS(XS)和PT(XT)为源域和目标域的边缘概率分布（下面简写为PS和PT）。令QS(YS|XS)和QT(YT|XT)为条件概率分布，下面简写为QS和QT。实际上，PS和PT以及QS和QT通常是不相等的，领域自适应迁移学习致力于从原始数据集XS、XT中重构出新的数据集，即进行特征迁移，使得：

MMD 最早被用来进行双样本的检测（two-sample test）问题[25]，以此来判断a和b的两个分布是否相同。其基本假设是：对于所有以分布生成的样本空间为输入的函数f，如果两个分布生成的足够多的样本在f上的对应的像的均值都相等，那么可以认为这两个分布是同一个分布。现在MMD 一般用于度量两个分布之间的相似性，它是基于两个分布之间的最大平均函数值差的有效非参数分布的距离测量。在判断两个分布a和b的时候，需要将观测样本首先映射到再生核希尔伯特空间（reproducing kernel Hilbert space，RKHS），然后再判断。假设Xa和Yb分别是从分布a和b通过独立同分布采样得到的两个数据集，数据集的大小分别为m和n。基于Xa和Yb可以得到MMD 平方的经验估计为：

针对领域自适应迁移学习，源域和目标域之间的分布差异以经验MMD 距离作为评估标准。可定义如下的边缘MMD 和条件MMD 来度量分布之间的差异：

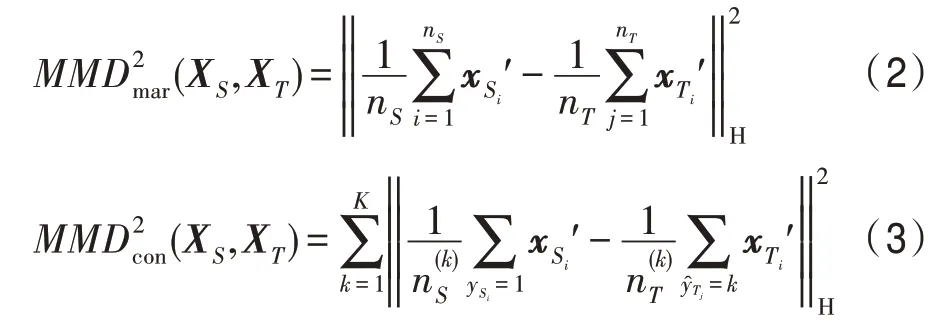
其中，XS、XT分别表示源域和目标域数据集；表示重构出的新数据集；表示重构后的源域的第i个样本数据；表示重构后的目标域的第i个样本数据。在条件MMD 中，ySi表示源域第i个样本的标签；yTj表示第j个目标域样本的标签；K表示样本的类的总数分别表示源数据和目标域数据第k类样本的数量。

2.2 流形正则化

流形正则化[26]最早是由Belkin、Niyogi、Sindhwani于2006年提出。在流形正则化中，用到了谱方法来表示几何信息。流形正则化可用于挖掘数据之间的拓扑结构。可以表示为：

其中，X表示多个样本组成的数据集；xi、xj表示原样本的特征；xi′和xj′是特征变换后的新特征；W是图邻接矩阵，表示每两个样本点之间的相似度。

2.3 经典TSK 模糊系统

模糊系统是基于模糊规则和模糊逻辑推理的非线性建模系统，其中知识库由if-then 模糊规则组成。模糊系统的显著特点是引入模糊集和模糊逻辑来模拟人类推理，并将不确定的语言专业知识转化为精确的数学表达式[27]。经典模糊系统包括Takagi-Sugeno-Kang 模糊系统（TSK-FS）、Mamdani-Larsen 模糊系统（ML-FS）和广义模糊系统GFS（generalized fuzzy system）[28-29]。其中，TSK-FS 由于其在实际应用中的高效性和灵活性而被广泛研究[30-31]。

一个有M条模糊规则的规则库的TSK 模型中，每条规则有p个前件，其中第i条规则可以表示为：

TSK FLS 的第z维输出yTSK,z(x)可表示为：

其中，fi(x)是规则的强度，定义为：

其中，T表示t-范数，通常取最小或者乘积，在式（6）和式（7）中，x表示应用于TSK FLS 的一个特定的输入。式（7）可以归一化为：

最常用的对应的模糊隶属度函数为高斯函数，即：

其中，k=1,2,…,p,i=1,2,…,M，和是由训练得到的前件参数。中心参数和宽度参数可以使用不同的方法估计。例如，当采用模糊C 均值（FCM）聚类算法对上述参数进行估计时，和可由下式给出：

这里的i表示数据维度，j表示训练样本编号，ujk是由FCM 得到的输入向量xj属于第k类的隶属度值，N是训练数据的个数。在式（11）中，h是可调参数，其可以手动设置或通过采用某种学习技术确定，例如常用的交叉验证策略。

当TSK-FLS 的前件参数给定，根据式（6）可以得到TSK 模糊系统的第z维输出为：

这里g(x)与c都是(p+1)M维向量，其构造过程如下：

令xe=(1,xT)T，则：

基于上述变换，令C=[c1,c2,…,cz]，则模糊系统得到的多输出向量可表示为：

3 融合模糊推理和流形正则化分布的特征迁移模型

本章将介绍一种具有良好解释性的方法，即FIMR-FTL，该方法可以在提升性能的同时，为实现非线性迁移提供良好的解释性，其框架如图1 所示。算法细节如下。

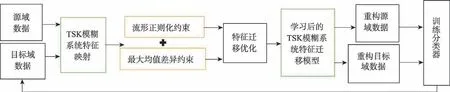
Fig.1 FIMR-FTL model framework图1 FIMR-FTL 模型框架图

3.1 FIMR-FTL 目标函数构造

FIMR-FTL 模型所用数据集为2.1 节所定义的数据集，源域S有标签，目标域T无标签，nS和nT是源域和目标域样本个数。

迁移学习的主要目的就是消除两个不同域数据的分布差异。基于此，FIMR-FTL 目标函数如下所示:

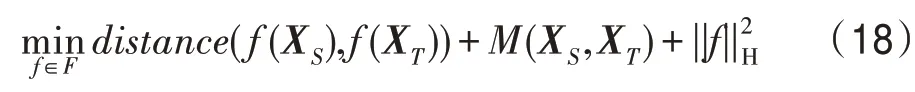
其中，第一项为分布差异项，函数f是特征映射函数，distance(f(XS),f(XT))表示源域和目标域经过映射后，在新的特征空间的差异，通过最小化该项可以使映射后所得源域及目标域数据尽可能相似。M(XS,XT)为流形正则化项，该项使得目标域进行非线性变换（即TSK 模糊系统输出）后的数据分布的几何形状尽可能小地产生变化，即映射前后数据信息变化尽可能小，最大限度上保留原始信息。为正则化项，降低过拟合的风险。各项具体形式如下。

3.2 TSK-FLS 特征映射

TSK-FLS 特征映射如图2 所示。图2 的TSK 模糊系统是一个多输入多输出系统，其输入是原始空间特征，其输出是通过模糊系统非线性映射得到的新特征。

3.3 最大均值差异约束构建

本文方法的关键之一在于构建式（18）中的distance 度量。为了能够直观地判断两个数据分布的差异，本文将最大均值差异用作此度量，即：

根据式（2）首先定义了源域和目标域在新特征空间的边缘分布MMD：

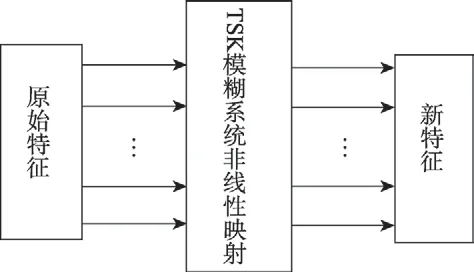
Fig.2 Feature mapping with TSK fuzzy system图2 TSK 模糊系统特征映射流程

这里，φ(xSi)=CTg(xSi),φ(xTj)=CTg(xTj)，均为经模糊映射后所得特征，可由式（17）计算。

定义XN=[x1,x2,…,xN],根据式（13）可以得到GN=[g(x1),g(x2),…,g(xN)]为(p+1)M×N矩阵。

基于XS、XT和式（14），则有：

令X=[XS,XT],G=[GS,GT]，根据式（17）能够得到TSK 模糊系统的多输出：

则式（20）可以写成如下的矩阵形式：

这里O为如下(nS+nT)×(nS+nT)的矩阵：

进一步考虑到仅仅减少域之间的边缘MMD可能不能全面地减少两个域之间的差异，因为边缘MMD并没有充分利用源域数据的标签信息。为了充分利用可用的数据集，还应将源域的类标签知识迁移到目标域以改进数据重构，因此进一步地添加条件MMD 项。

根据式（3）可定义源域和目标域在新特征空间的条件分布MMD，即：

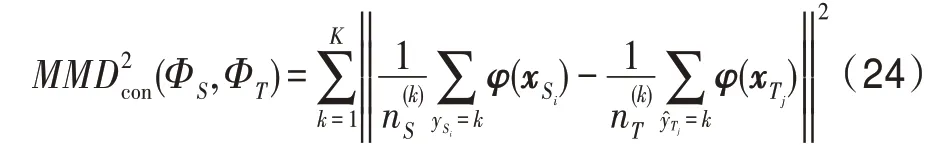
同理，可以将其写成矩阵的形式：

这里Ok是定义如下的(nS+nT)×(nS+nT)矩阵：

最后将条件MMD 和边缘MMD 相结合，得到联合MMD 的近似逼近的矩阵形式为：

3.4 流形正则化约束构建

期望原始空间中的数据点之间的拓扑关系保留在新的特征空间中，即最大程度上保留原始信息。为此，采用流形正则化来保持源域和目标域的流形结构，参考式（4），构造如下流形正则化项：

这里，xSi表示源域的第i个样本；xTi表示目标域的第i个样本；φ(xSi)表示样本xSi经过映射得到的新特征；LS、LT表示两个域的图拉普拉斯矩阵，定义如下：

其中，DS、DT是对角矩阵，I是单位矩阵，WS、WT是图邻接矩阵，它们表示源域和目标域内每两个样本点之间的相似度，令L=diag(LS;LT),D=diag(DS;DT)则有L,D∈R(nS+nT)×(nS+nT)。

其中，Ep(xi)表示样本xi的P个最近邻样本集合。考虑到欧式距离使用最为广泛，本文亦采用欧式距离作为衡量标准。

3.5 特征迁移优化目标及其求解

根据式（18）、式（27）和式（28），得到最终FIMRFTL 的优化目标函数：

对于式（31），可将其转化为如下等价的广义特征值分解[32]问题：

通过式（32）即可获得TSK 特征变换模型的参数，利用式（21）可对目标域数据和源域数据进行重构，并且将重构后的目标域和源域数据训练相应的分类器模型，根据分类器可对目标域数据进行标注，然后根据标注结果以迭代的方式对TSK 特征变换模型进行再次学习。

算法1 给出了FIMR-FTL 特征迁移方法的算法流程。

算法1FIMR-FTL 算法

1.初始化：设置规则数M，平衡参数α、β，新特征空间维度Z。

2.构建MMD 矩阵O，令Ok=0,k=1,2,…,K，迭代次数T。

3.Fort=1:Tdo

Ift=1，使用边缘MMD

else，使用联合概率分布

4.利用TSK 模糊系统得到矩阵G，根据式（32）求得C，然后重构数据集X′。

5.用重构后的源域样本训练分类器，并给目标域XT加上伪标签。

6.End for

7.得到最终的TSK 特征迁移模型。

4 实验

本章对特征迁移图像分类问题进行了大量实验，以评估提出的融合模糊推理和流形正则化的特征自适应迁移学习方法。

4.1 数据准备

在本文中一共用到了COIL20、MNIST、USPS、Office-Caltech-256 数据集进行训练和测试（https://github.com/jindongwang/transferlearning/blob/master/data/dataset.md#office+caltech）。这些数据集都是计算机视觉领域自适应问题中广泛使用的基准数据集。

表1 表示实验所用的8个基准数据集，包括了它们的样本数、特征维度、类别数，下面给出数据集的详细介绍。

Table 1 8 benchmark image datasets表1 8个基准图像数据集

COIL20 包含了20个物体，1 440个图像。实验中，将该数据集分为两个子集，即COIL1 和COIL2。COIL1 包含象限1 和象限3 上拍摄的所有图像；COIL2 包含象限2 和象限4 方向拍摄的所有图像。用这种方法使得子集COIL1 和COIL2 遵循相对不同的分布。然后分别将源域和目标域两两设为COIL1、COIL2，组成两组迁移对，即COIL1-COIL2 和COIL2-COIL1，它们分别表示从COIL1 迁移到COIL2 的过程和从COIL2 迁移到COIL1 的过程。

USPS 和MNIST 是手写体数据集，为了加快实验进程，通过在USPS 中随机采样1 800个图像来构建一个新的数据集USPS，然后从MNIST 中随机采样2 000个图像组成新的MNIST 数据集。将所有图像重新缩放成大小为16×16，并且通过编码灰度像素值的特征向量来表示每个图像。这里也将手写体数据集组成两组迁移对，即USPS-MNIST 和MNIST-USPS。

Office 数据集是一个用于领域自适应的基准数据集，包括46 522个图像，这些图像来自于3个不同的域：（1）AMAZON 是亚马逊在线商家下载的图像；（2）Webcam 是通过网络摄像头获取的低分辨率图像；（3）DSLR 是从数码单反获取的高分辨率图片。Calteh-256 是标准的图像识别数据集。这4个数据集分别简写为A、W、D、C。在实验中，采用了Gong 等人[15]发布的公共Office+Caltech 数据集。SURF 特征被提取并量化为800-bin 直方图。通过选择两个不同的域作为源域和目标域，来构建12 组跨域数据集，例如C→A，C→W，…，W→D。

4.2 实验设置

实验中将提出的方法与5 种现有的特征迁移方法进行了比较，分别是TCA、GFK、TSL、JDA、TJM。为了保证实验结果的统一性，实验中采用的分类器均为1NN 最近邻分类器。

联合FIMR-FTL 模型设置的参数分两部分：一部分是经典TSK 模糊系统的参数；另一部分是约束条件的参数。首先，为保持系统的简洁性和可解释性，TSK 模糊系统的模糊规则数在区间[2,16]内以2 为步长寻优，根据经验将用于生成前件参数的高斯模糊隶属度函数的宽度调节参数h设置为1。生成前件参数的聚类算法使用的是TSK 模糊系统中常用的FCM聚类算法。其次，约束条件的两个平衡参数是α和β，α表示最大均值分布差异项的权重，β表示流形正则化项的权重，z是新特征空间维度，并且将所有需要迭代的算法迭代次数统一设为10。

按照表2 中所示设置各个算法中的参数。对于TCA、TSL 和JDA 方法，使用了文献[24]里的参数设置和实验结果，TCA和TSL其实可以看作是JDA的特例，TCA是没有考虑条件MMD的JDA，而TSL则是采用Bregman 散度而不是MMD 作为比较分布的距离。

4.3 实验结果及分析

本文实验结果指分类准确率均值和标准差。表3给出了不同特征迁移方法结合1NN得到的在不同数据集上的分类准确率。表格中每个数据集上得到的最佳结果以粗体显示。下面给出分类准确率的计算公式：

表3 给出了各类方法在16个数据对上的平均性能。从中可以看出，联合FIMR-FTL 方法的平均准确度达到了63.18%，是所有方法中准确率最高的。在16 项数据迁移对中，本文方法在Office-Caltech-256数据集对应的12 项数据迁移对上得到的效果明显优于其他方法。与最佳基准方法TJM 相比，FIMR-FTL对16 项任务的平均准确率提高了5.82%。可见，将TSK 模糊系统引入到迁移特征学习中不仅使得迁移效果得到不小的改善，而且很好地解决了存在的非线性特征迁移方法在使用核等技巧时面临的难以理解特征构建过程的问题。除了在USPS 和MNIST 数据对上性能一般外，本文方法在COIL20 数据集对应的迁移数据对上依然保持了较高的准确率。而造成性能一般的原因则可能是由于USPS 和MNIST 数据集都是数字数据集，数字数据集相对于其他数据集来说更加稀疏。在使用TSK 模糊系统进行特征映射的时候，数据集稀疏导致在进行矩阵运算时计算误差较大，影响了算法的性能。

Table 2 Algorithm parameters setting表2 设置算法参数

Table 3 Comparison of classification accuracy between proposed algorithm and other feature transfer algorithms表3 本文算法与其他特征迁移算法分类正确率比较

表3 中，对比算法由于不存在随机性且测试数据集是固定的，因此相同参数下得到的结果没有变化，即标准差为0。对于本文方法，表4 给出了在相同参数设置下，单独使用边缘MMD 和单独使用条件MMD 的FIMR-FTL 模型与联合FIMR-FTL 的实验结果。由于本文方法在构造模糊系统时引入的FCM 聚类具有一定的随机性，因而每次训练所得模型具有一定的差异性。表中给出了5 次实验结果的均值和标准差。由于Office-Caltech-256 数据集在TSK 模糊系统映射时，多次实验得到的映射之后的特征矩阵变化较小，从而导致多次实验的分类准确率没有变化，因此在Office-Caltech-256 数据集上，本模型5 次实验的标准差均为0。这也说明了在该数据集下本模型十分稳定，而在USPS 和MNIST 手写体数据集和COIL20 数据集上虽然得到了5 次不同的结果，但标准差都很小，体现了本模型应对不同数据集时具有一定的普适性和稳定性。

Table 4 Experimental results of 3 MMD models表4 3 种MMD 模型的实验结果

与联合FIMR-FTL 模型不同的是，由于只使用边缘MMD 的情况下不需要使用源域标签，因此边缘FIMR-FTL 模型在实验过程中不需要进行多次迭代。而在条件FIMR-FTL 模型里，由于需要给目标域添加伪标签，需要先通过源域数据训练分类器给目标域添加伪标签，然后使用条件MMD 进行迁移训练，不断迭代更新伪标签。

从表4 中可以看出，联合FIMR-FTL 模型的平均准确率实验效果最优，而在16 组迁移实验中，联合FIMR-FTL 模型最优次数也达到了10 次，边缘FIMRFTL 模型和条件FIMR-FTL 模型则分别是2 次和4次。也就是说，在绝大多数情况下联合FIMR-FTL 模型的实验效果要优于边缘FIMR-FTL 模型和条件FIMR-FTL 模型的，这里也验证了联合FIMR-FTL 模型的有效性。

4.4 参数敏感度分析

为了分析参数的敏感度，并考虑到实验的简洁性，选择A-C、W-D 两组数据对进行了分析。

为了探究规则数M对本文方法的影响，实验中将其他参数固定，只变化规则数M。图3 示出了不同规则数下的性能。从图中可以看出，不论是数据对A-C，还是W-D，实验的结果都是先随着规则数的增加，准确率大幅上升，接着随着规则数变化上下波动，并慢慢趋于平缓。从图3 中可以看出规则数M对实验结果的影响很大。

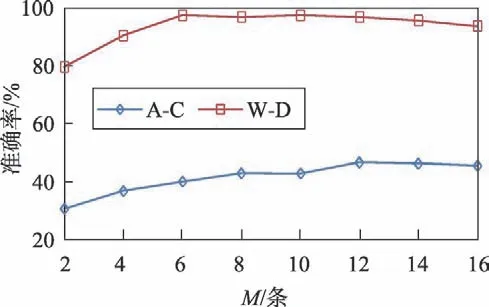
Fig.3 Influence of the number of rules M图3 规则数M 的影响

图4 表示新特征空间维数对分类性能的影响。首先从图中可知，在A-C 数据对上，维度为30 时达到最优效果，在W-D 数据中，维度为20 的时候达到最优，因此在不同数据集下，达到最优准确率的维度是不同的。其次针对数据集W-D，z的影响比较大，但是针对数据集A-C，z的影响相对比较小，也就是说，对不同数据集，新特征空间维数z的影响效果也不同。

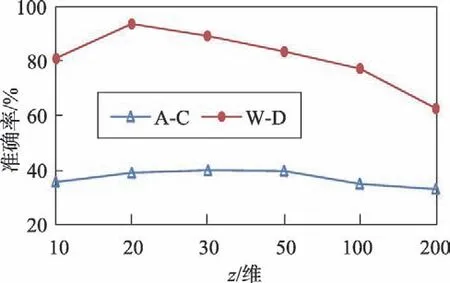
Fig.4 Influence of new spatial mapping dimension z图4 新空间映射维度z的影响

5 总结

本文提出了一种基于不确定推理规则的特征迁移方法。与其他算法不同，为了使提出的方法具有良好的解释性和良好的非线性特征学习能力，引入了TSK 模糊系统。为了避免信息损失，进一步引入了流形正则化技术来保持数据流形，并通过减少MMD 距离来更好地匹配目标域和源域的分布。实验证明提出的FIMR-FTL 算法较之一些已有方法具有更好的性能。未来拟对提出方法的参数选择进行更深入的研究。