基于核心素养培养的中职数学教学实践

高晓兵 翟朝纪

(广西北部湾职业技术学校 536000)

《关于对中等职业学校《数学》等七个课程标准征求意见的通知》(教职成司函〔2018〕161号)明确数学的学科核心素养，应是具有数学基本特征的思维品质、关键能力和情感、态度与价值观的综合体现，主要包括了数学运算、直观想象、数据分析、逻辑推理、数学抽象和数学建模.笔者在教学实践中，非常重视这6种核心素养的培养，下面结合自己的教学实例，谈谈源自一线的教学培养实践和感悟.

一、训练数学运算能力，以“等差数列的前n项和”的教学为例

例1 养猪场向银行贷款36000元，还款方式是第一个月还1000元，以后每个月比前一个月多还200元，请问需要多少个月才能还清全部贷款？

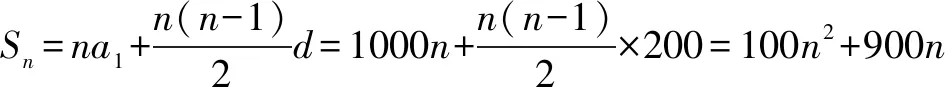
直接计算既然是每个月还贷款的问题，那完全可以将每个月还款的情况，用一张表格将它们列出来，并将已经累积的还款统计出来，逐月列出、累计出来，直到还清36000，就可以直接得出需要多少个月能还清全部贷款.表格如下：

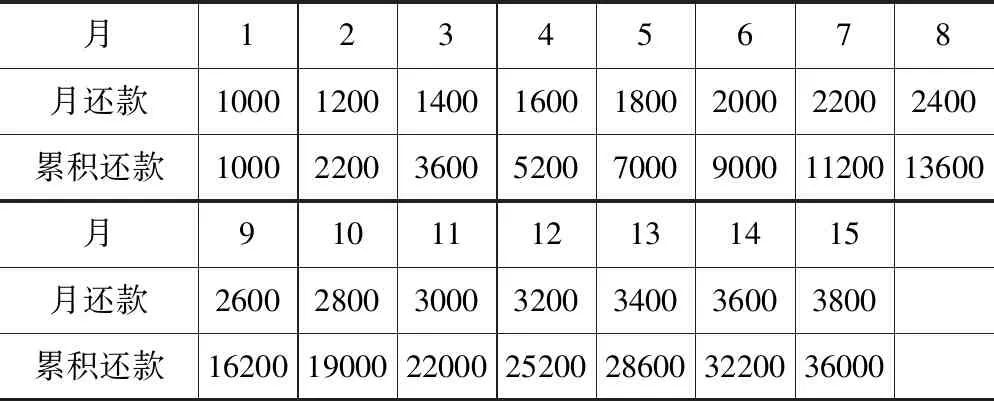
月12345678月还款10001200140016001800200022002400累积还款1000220036005200700090001120013600月9101112131415月还款2600280030003200340036003800累积还款16200190002200025200286003220036000

培养感悟在中职学校，教师很有必要重视、加大数学运算的教学和指导力度，尤其要考虑一些有效的办法，引导学生进行有效运算，比如：对于数的加、减、乘、除等，宜引导学生养成“符号+数字”分类处理的习惯.同时，也可以引导学生进行积极思考，用一些较直接的办法，直接将答案计算出来，适度避开较繁杂、没掌握的运算公式、求解过程.

二、训练直观想象能力，以“直线与平面的位置关系判定”的教学为例

例2 下列判断正确的是( ).

A.若两条直线l1,l2都与平面平行，则l1∥l2；

B.若一条直线l与两直线l1,l2都垂直，则l1∥l2；

C.若一条直线l与两个平面α,β平行，则平面α∥平面β；

D.若一条直线l与平面α平行，则直线l与平面α内无数条直线平行.

教学策略一是引导学生明确“平行”的核心关键词为“在同一平面内没有交点”，便于在空间内，有理有据地判定是否平行；二是引导学生充分发挥“教室”的空间状态以及借助现有的物品，进行直观想像.比如：将书桌的台面视作一个平面，将两支笔视作两条直线进行摆放，会有“交叉两支笔，平行悬于桌面上方”，故A错误；引导学生拿起文具盒，会发现“某一顶点引出来的三条直线，其中一条都会与另两条垂直，但这两条直线是垂直的”，B错误；引导学生将教室的一灯管视作直线，会发现“灯管与天花板平行，也会与墙壁平行，但是天花板与墙壁不平行”，C错误；用一支笔平行悬于书桌上方，后在桌上摆放多支笔，会发现这些笔也是平行的，知D正确.

培养感悟对于几何问题，很多学生动手画图，尤其是立体图形的能力偏弱，但是学生们爱动脑、善于观察，教师可以引导学生细心去观察教室、学习用具、生活用品等，将几何问题进行直观化的观察.当然，在教学过程中，有必要加强数形结合的思想渗透，比如：三角函数在各象限的符号问题，引导学生借助平面直角坐标系，就能很直观明确出来.

三、训练数据分析能力，以“频次”的教学为例

例3 某射手在同一条件下进行了6轮射击，每轮的射击次数和击中靶心的情况如下表所示：

射击次数102050100200500击中次数9194491178451

问：(1)求每一轮这个射手击中靶心的频率；(2)这个射手射击一次，击中靶心的概率约是多少？

教学思路第一步，引导学生读懂题目，尤其是准确地读懂表格，明确每一轮的射击次数和击中靶心次数；第二步，引导学生读懂问题，联系“击中靶心的频率=中靶心的次数射击次数”的知识要点，得到这六轮击中靶心的频率分别为910=0.9、1920=0.95、4450=0.88、91100=0.91、178200=0.89、451500=0.902；第三步，引导学生走出“击中靶心的概率=每一轮击中靶心的频数之和射击轮数6”[即：(0.9+0.95+0.88+0.91+0.89+0.902)6]的误区，得出正确的数据分析结果[即：(9+19+44+91+178+451)(10+20+50+100+200+500)=0.9].

培养感悟在数据时代，需要每一个人都具备一定的数据收集、整理、提取重要数据信息以及分析能力.中职生在学习专业技能时，也需要有敏锐的数据意识，教师在教学过程中，不妨将它作为一项课堂甜品，融入到平时的教学中，毕竟数据分析的内容编排得太后，很多学校并没有讲到这一内容.

四、训练逻辑推理能力，以“充要条件的判定”的教学为例

例4x6是x8的( )条件.

A.充要 B.充分不必要

C.必要不充分 D.既不充分也不必要

教学思路在多年的教学实践中，笔者发现：多数中职生不明确什么情况下是(不)充分、(不)必要，经常发生混乱.为了帮助学生进行有条理的理性思考，引导学生按照“确定好：关注谁——主动推，判：(不)充分——被动推，判：(不)必要”的逻辑来推理，综合明确：是什么条件.本题，关注：x<6——主动推x<6⟹x<8(成立)：充分——被动推x<8⟹x<6(不成立.理由：7<8⟹7<6，7小于6是不对的)：不必要——综合知：x<6是x<8的充分不必要条件，选B.

培养感悟在教学过程中，笔者除了引导学生养成一些科学、合理的逻辑推理、思维习惯以外，还会积极融入一些数字推理、逻辑推理小游戏等，切实帮助学生提高逻辑推理和思维能力.

五、训练数学抽象能力，以“始终边相同的角”的教学为例

例5 (1)下列各组角中，终边相同的是( ).

教学分析通过借助动作——旋转，角从0到360进行了有效扩张，顺时针“旋转”出了负角，而逆时针不断地“旋转”会得到370等更大的角，但无论如何，角会涉及两个边——始边、终边.对于始边和终边都相同的两个角α、β，看起来有点抽象、不够明了，这时不妨定住一个角α，接着用角α的终边去“旋转”，试着旋转后发现：角α在旋转的时候，必须一圈一圈地转满，终边才和角α的终边相同.接着，可以将这一情形进行抽象归纳：让角α“转圈圈”找到始、终边相同的角β，转一圈360(或2π).紧接着，解题：(1)390(逆时针转1圈)+360，到750，知A项错；-330(逆时针转1圈)+360，30(逆时针转1圈)+360，390(逆时针转1圈)+360，到750，故选B.当然，对于C、D项，也可以按此方法进行核实.最后，解题：(逆时针转1圈)+2π(即到易知A、B都不符合；(顺时针转1圈)-2π(即：到知C项符合，选C.

培养感悟中职学生的抽象思维能力偏弱，但是他们的感性认识能力很足，对直观、形象、有趣的事物很有兴趣，为此笔者建议：教学不妨多考虑从具体的事物入手，逐步引入、带入、深入，并帮助他们对抽象的事物进行数学表达、概括.比如：在讲函数的单调性时，可以先引导学生看具体的图形，对递增、递减有较具体、深刻地认识，后对增(减)函数进行抽象的数学诠释.

六、训练数学建模能力，以“函数的实际应用举例”的教学为例

例6 某招待所有200个床位，每床每天需10元洗护费，每天租金70元时，每天客满，当日租金每增加1元时，则床位出租数会减少2个，问招待所将日租金定为多少时，每天盈利最高，最高盈利是多少？

读题分析假定日租金为x元时，知：日租金提高了(x-70)元，又由“当日租金每增加1元时，则床位出租数会减少2个”，从而知：每天减少2(x-70)个出租床位，进而知：每天租出去200-2(x-70)个床位，即340-2x个床位.

建立模型通过以上分析，可以明确“每天盈利与日租金存在函数关系”，可以建立起数学模型来解答：y=x(340-2x)-200×10,x≥0.

求出答案通过配方、化简的办法，得

y=-2(x2-170x)-2000=-2(x-85)2-2[-(-85)2]-2000=-2(x-85)212450≤12450.

从而知：当x-85=0，即x=85时，y取到最大值12450.所以日租金定为85元时，每天最高可盈利是12450元.

培养感悟中职数学的学习一定要联系生活、贴近实际、服务专业，能够用数学知识来解决一些实际的问题，在很多时候，需借助构建数学模型，当然更多的是函数模型.笔者认为在中职教学实践中，教师要重视函数的应用教学，引导学生读懂、弄通题意，寻找好函数的关系，建立好函数模型，然后进行解答.