恒成立问题的多角度思考

徐照武

(广东省珠海市实验中学 519090)

恒成立问题，覆盖了函数、导数、不等式、三角、数列、解析几何等高中数学的很多知识点，还涉及到一些重要的数学思想方法.多方位多角度归纳总结这类问题，对提高对恒成立问题的认识及分析问题和解决问题的能力很有帮助.

一、恒成立溯源

这是一个古老问题，我们很少注意挖掘其来历，其实它历史悠久，来源于一元二次方程，这是我们很少注意到的.请看下面问题：

(1)已知方程2x2-ax+1=0无实根,求实数a的取值范围.

(2)已知函数f(x)=2x2-ax+1>0对任意实数x都成立,求实数a的取值范围.

(3)已知函数f(x)=-x3+ax2-x-1在R上是单调函数,求实数a的取值范围.

(1)是我们非常熟悉的一类题目，但若改为(2) (3)的叙述方式，实际就是恒成立问题.

二、高考试题中多次出现恒成立问题

1977年，恢复高考制度以来多次出现恒成立问题，如1990全国高考理数的压卷题的第一问：

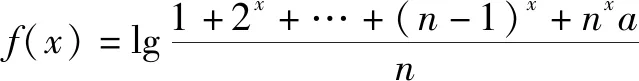
解析题目看似函数定义域问题，其实变换后是恒成立问题.

简解f(x)当x∈(-,1]时有意义的条件是：

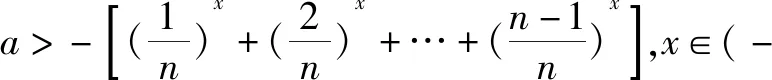
此题有一定难度.但可以说，以后的恒成立问题基本来源于此.

三、恒成立易错的地方

例2已知对∀x∈R,k≥sinx+cosx均成立，求k的最小值.

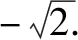
四、恒成立的分类及求解方法

1.a≥f(x)型

此类问题常利用最值法，即a≥[f(x)]max(如例2).

例4(2018全国一卷，选修4-5：不等式选讲)已知f(x)=|x+1|-|ax-1|.

(1)当a=1时，求不等式f(x)>1的解集；

(2)若x∈(0,1)时不等式f(x)>x成立，求a的取值范围.

(2)当x∈(0,1)时|x+1|-|ax-1|>x成立等价于当x∈(0,1)时|ax-1|<1成立．

若a≤0，则当x∈(0,1)时|ax-1|≥1；

综上，a的取值范围为(0,2]．

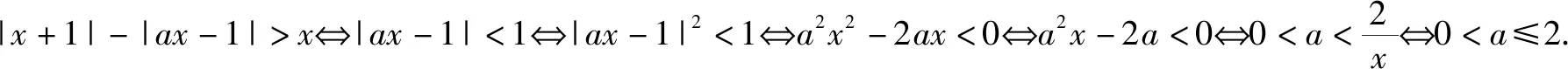
2.f(x，a)≥0型(即混合型)

一般有两个途径：分离变量转化为a≥f(x)的形式，或利用[f(x,a)]min≥0求解.

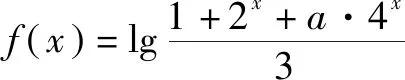
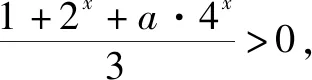
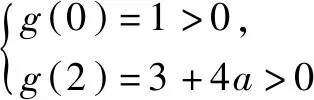
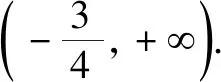
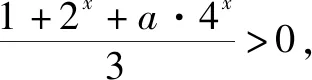
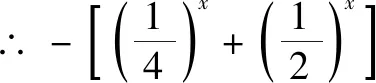
3.f(x，y)≥0型(即多变量型)

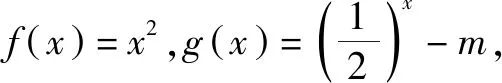
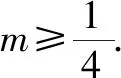
注：此类问题的条件∀x1∈[-1,3]，∃x2∈[0,2]可以有多种组合：∀x1∈A,∀x2∈B；∀x1∈A,∃x2∈B；∃x1∈A,∀x2∈B；∃x1∈A,∃x2∈B，因此就会有不同形式的题目.

例7(2012陕西理科21题(2))设函数f(x)=x2+bx+c(b,c∈R),若∀x1，x2∈[-1,1]都有|f(x1)-f(x2)|≤4，求b的取值范围.

分析与解此题即|f(x1)-f(x2)|的最大值≤4，而|f(x1)-f(x2)|的最大值就是f(x)在[-1,1]上最大值与最小值的差M.

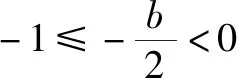
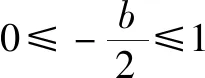
综上可知：-2≤b≤2.

4.其它类型

下面一些学生熟悉的题目其实也是恒成立问题，只是我们平时不注意罢了.

(1)函数f(x)=lg(x2-ax+2)的定义域为R,求实数a的取值范围.

(2)函数f(x)=lg(x2-ax+2)的值域为R,求实数a的取值范围.

(3)函数f(x)=ax-1-1(a>0且a≠1)的图象过定点____.

(4)直线x-ay+2a=0过定点____.

(5)12+22+32+…+n2=an3+bn2+cn+d对任意的正整数n都成立，求常数a,b,c,d的值.

(6)函数f(x)=-2x3+ax2+bx+c-1是奇函数，求实数a,c的值.