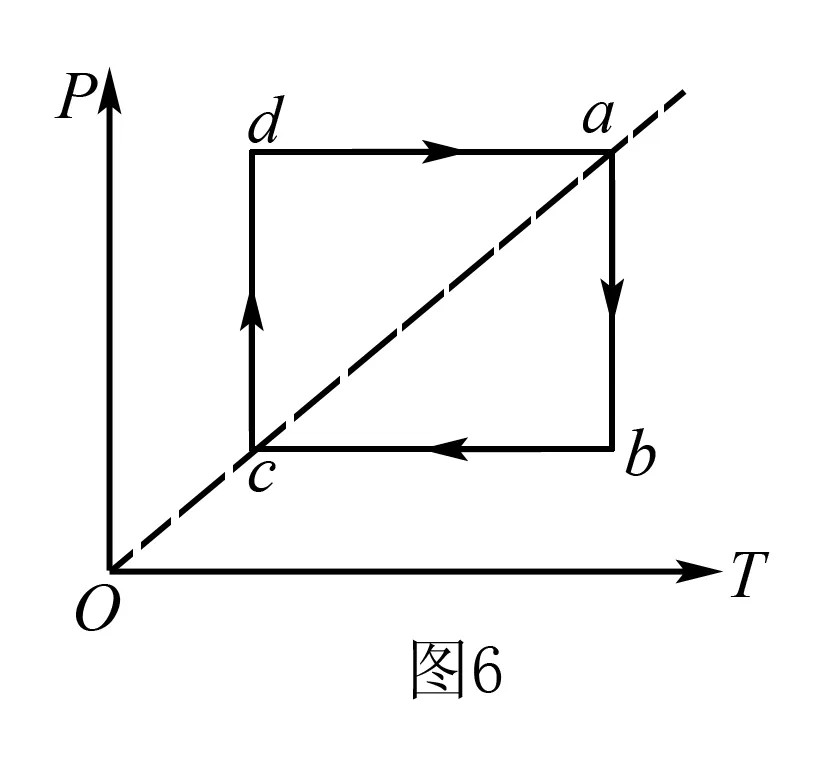
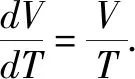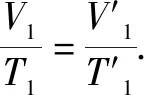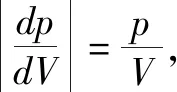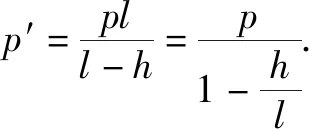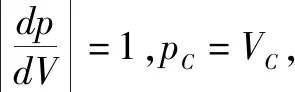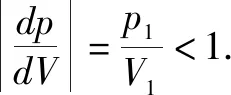理想气体状态方程微分式及其应用

许冬保

(江西省九江第一中学 332000)

一、理想气体状态方程微分式

设某理想气体在温度为T时，压强及体积分别为p、V.由克拉珀龙方程知pV=nRT，式中n为摩尔数，R为摩尔气体常量.

假设气体的质量不变(或n不变).对该式两边进行微分运算，可以得到d(pV)=nRdT，即pdV+Vdp=nRdT

下面对该式作些讨论.

1. 查理定律微分式

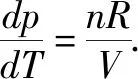
2.盖—吕萨克定律微分式

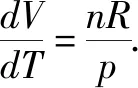
3.玻意耳定律微分式

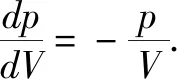
4.体积功的微分式

假设气体发生准静态过程，且气体的压强保持不变，当体积变化dV时，因体积变化所对应的元功为dW=pdV.结合克拉珀龙方程微分式，得到dW=nRdT.

二、应用

1.水银柱移动问题的分析

例1 如图1所示，两容器用水平细管相连，容器内装有温度均为T的同种理想气体.若管中有一小段水银柱将A、B两部分气体隔开，现使A、B同时升高温度，若A升高到T+ΔTA，B升高到T+ΔTB，已知VA=2VB，欲使水银柱向右移动，则 ( ).

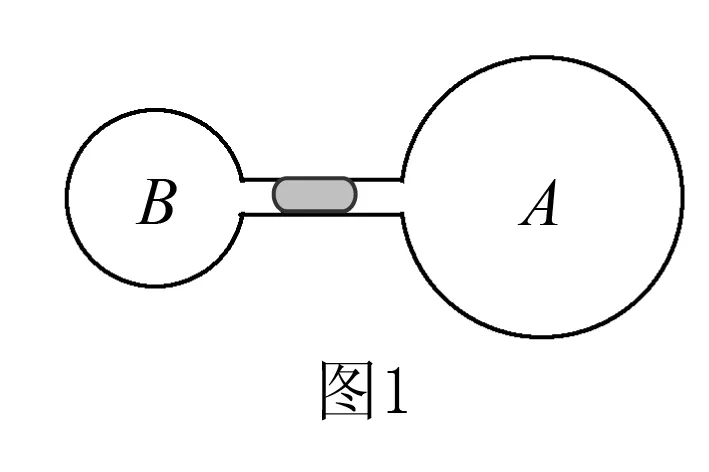
C.ΔTA<ΔTBD.ΔTA>ΔTB

分析A、B两部分气体温度升高时，两部分气体的体积不变，假设压强的增加量分别为ΔpA、ΔpB.由查理定律的微分式，有

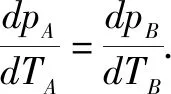
欲使水银柱向右移动，则dpA>dpB，即dTA>dTB或ΔTA>ΔTB.选项D正确.

点评水银柱移动问题涉及气体压强、体积和温度三个量的变化，常用假设法进行分析.假设温度变化时水银柱不动，通过比较水银柱两侧气体压强的增量，来判断水银柱移动的方向.或反过来由水银柱移动方向来判断温度变化的情况.解题方法上也常选择p-T图像进行直观分析.

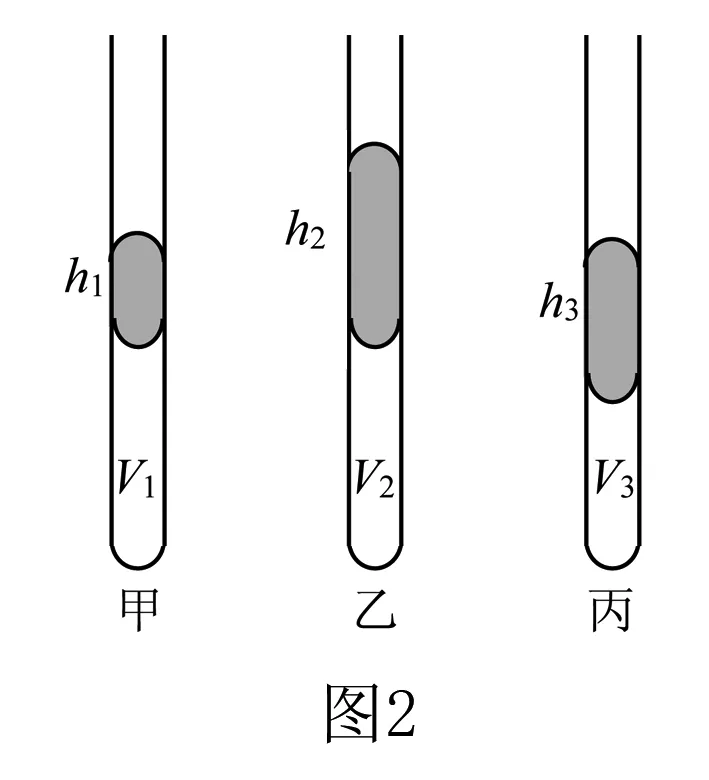
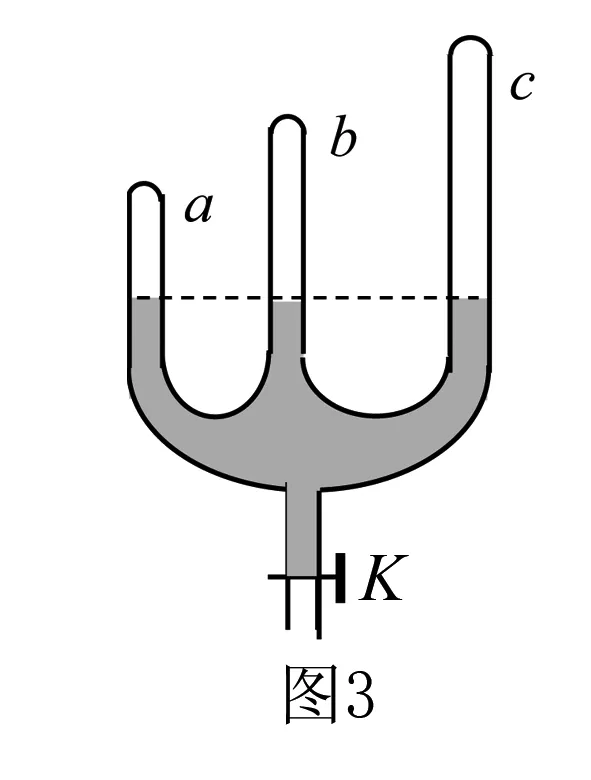
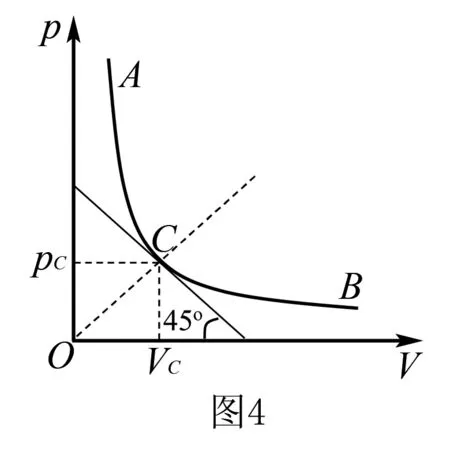
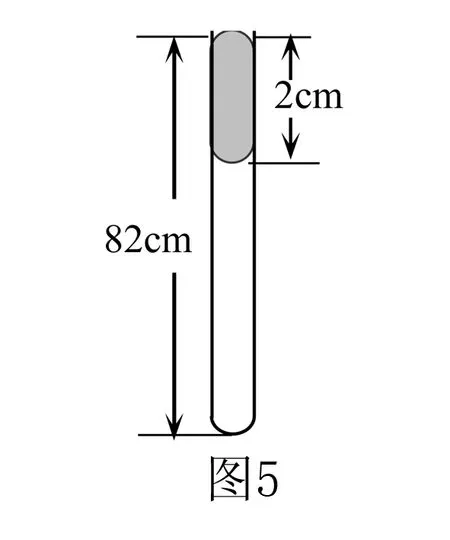
例2 如图2所示，三根粗细均匀的细玻璃管，中间均用一段水银柱封住温度相同的空气柱，且V1=V2>V3，h1

A.丙管 B.甲管和乙管

C.乙管和丙管 D.三管上移一样多

例3 如图3所示，底部连通的均匀玻璃管a、b、c，上端封闭，原先三管中水银面处在同一水平面上，如果再从底部缓慢注入稍许水银，则三管中水银面高度的情况为 ( ).

A.a中最高

B.b中最高

C.c中最高

D.一样高

2.水银柱注入问题的分析

例4 如图5所示，长度为82cm的粗细均匀的直玻璃管，内有齐口2cm长水银柱封闭一定质量的气体，已知外界大气压强为76cm Hg.已知环境温度不变，若从管口缓慢加入水银，则能注入多长的水银柱？

由玻意耳定律，有p1V1=p2V2.

代入已知数据，解得x=2cm(x=0，舍去)

点评由图5可进一步讨论：初态时，若管中空气柱的长度小于或等于管内气体的压强，则无法注入水银到管中，通过等温线中斜率的分析可以比较方便地讨论直玻璃管中水银柱的注入问题.

注意当p2=V2时，得到x=1cm.其对应的物理意义是，该条件下的气体温度高于题述所给的环境温度.

3.气体做功问题的分析

例5 一定质量的某种理想气体从状态a开始，经历等温或等压过程ab、bc、cd、da回到初始状态，p-T图像如图6所示.其中对角线ac的延长线经过坐标原点O.以下结论正确的是( ).

A.在a、c两状态气体的体积相等

B.在状态c时气体的内能等于它在状态a时的内能

C.在过程da中气体从外界吸收的热量大于气体对外界做的功

D.在过程cd中气体向外界放出的热量小于外界对气体做的功

E.在过程bc中外界对气体做的功等于在过程da中气体对外界做的功

分析仅对选项E进行分析.由图6可知：在过程bc中，压强不变，由体积功的微分式，得dW=nRdT，即Wbc=nRΔT；同理，在过程da中，压强不变，体积功为Wda=nRΔT.比较得到Wbc=Wda.选项ACE正确.

点评若由体积功的定义及玻意耳定律进行推导得到Wbc=Wda，过程烦琐.本题应用微分式处理，轻松得到dW∝dT，有效地提高了思维品质.