基于显式算法的RC框架结构抗地震倒塌能力分析

赵鹏举，于晓辉，陆新征

(1.哈尔滨工业大学结构工程灾变与控制教育部重点实验室，黑龙江，哈尔滨 150090;2.清华大学土木工程安全与耐久教育部重点实验室，北京 100084)

汶川地震的震害调查发现，许多钢筋混凝土(RC)框架结构，如居民住房和教学楼等，发生了较为严重的破坏甚至倒塌[1－2]。由于建筑结构发生倒塌是造成人员伤亡的主要原因，因此，合理评估建筑结构在地震作用下的抗倒塌能力一直是地震工程研究的热点。近年来，针对我国量大面广的RC框架结构的抗地震倒塌的设计[3]和能力评估[4]开展了一系列研究。

目前，结构抗地震倒塌能力评估的主要方法是增量动力分析(Incremental Dynamic Analysis, IDA)方法[5]。该方法选取一组地震动作为地震输入，通过对每条地震动进行调幅，最终获得结构发生倒塌所对应的地震动强度，并将其作为结构的抗地震倒塌能力。考虑地震动之间的不确定性，最终获得的结构抗地震倒塌能力通常体现为地震倒塌易损性的形式。我国学者采用IDA方法对RC框架结构的抗地震倒塌能力开展了一系列研究。例如：范萍萍等[4]对不同抗震设防烈度和抗震等级的RC框架结构进行了地震倒塌易损性分析，比较了不同抗震等级下框架结构的抗地震倒塌能力的差异。吕大刚[6]采用IDA方法，比较了分别采用FEMA准则和结构动力失稳点作为结构倒塌判据的RC框架结构地震倒塌易损性。于晓辉和吕大刚[7]将可靠度分析中的均值一次二阶矩法与IDA方法相结合，提出了一种随机IDA方法来考虑结构不确定性对地震倒塌易损性的影响。

要进行IDA分析，一个关键的问题是选择合适的结构动力学数值计算方法。在已有的结构动力学数值计算方法中，逐步积分法由于其简单高效的特点被广泛采用。逐步积分法分为隐式算法与显式算法。其中，显式算法无须求解联立方程组，对于多自由度结构以及非线性分析问题，与隐式算法相比，显式算法有更高的计算效率[8－9]。目前，显式算法已经被一些商业化软件所采用[10]，并在土木工程领域得到了一些应用。例如：陈国兴等[11]针对地铁地下结构比较了ABAQUS在并行计算时隐式算法与显式算法的计算效率与精度，表明显式算法具有远高于隐式算法的计算效率；梁艳晨等[12]基于ANSYS显式动力模块模拟了碎石垫层地基对框架结构抗震能力的提高。近年来，作为一种免费开放式有限元模拟软件平台，OpenSees软件得到了广泛应用。张书豪[13]基于蛙跳法提出了一种新的显式积分算法，并将该算法集成于OpenSees软件中，同时对该算法的精确性进行了验证。由于显式方法不存在隐式算法常有的收敛性问题，其在非线性分析计算时能更好地模拟结构的极限状态，也更加适合进行结构的抗地震倒塌能力的评估。

鉴于显式算法在进行结构抗地震倒塌能力分析中的优势，本文以OpenSees软件作为分析平台，采用文献[13]所提出的基于蛙跳法的显式积分算法，通过IDA方法对按我国规范设计的RC框架结构的抗地震倒塌能力进行了评估。在分析过程中，考虑了4种不同倒塌判据的影响，包括：我国《建筑抗震设计规范》[14]推荐的结构层间位移角限值θmax=1/50(判据1)、美国FEMA 356[15]推荐的θmax=4%(判据2)、文献[16]建议的IDA曲线切线刚度退化为初始刚度的20%(判据3)以及结构主要构件竖向倒塌位移超过1 m(判据4)。其中，当采用倒塌判据4时，结构已经进入强非线性，此时用显式算法可以很好地获得结构在这一状态附近的非线性状态，而隐式算法则会由于收敛性的问题无法逼近这一极限状态。

1 基于蛙跳法的显式算法基本原理

显式算法与隐式算法的主要差别在于显式算法是由已知数据来表示下一积分步的状态量(如式(1))，而隐式算法对下一积分步的状态量不能直接给出公式，需要通过解方程来求解(如式(2))[17]。

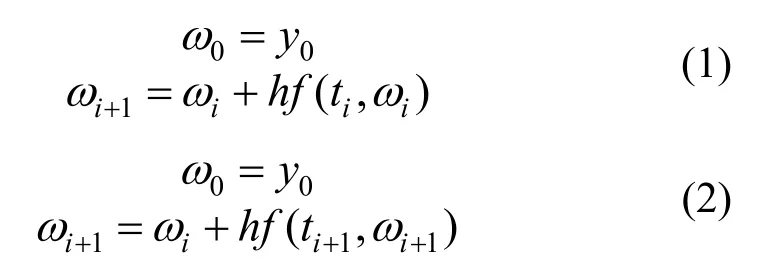
式中：ωi、ti、ωi+1与ti+1分别为第i个积分步与第i+1个积分步的状态量；y0为初值；h为步长；f表示导函数。

中心差分法[18]是基本的显式积分算法，其以有限差分在数值上代替求导。对于运动方程：

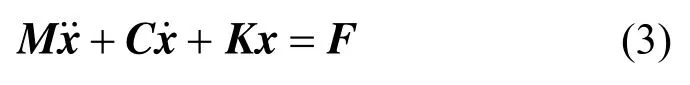
将其位移项进行泰勒展开可得：

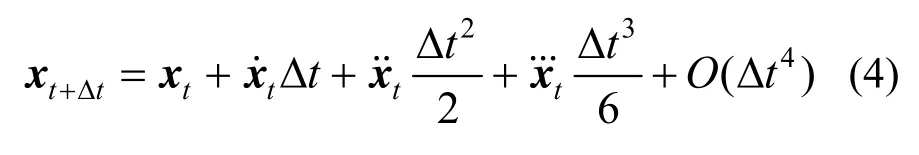
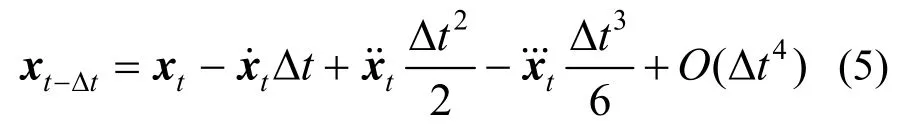
将式(4)和式(5)相加和相减并舍去高阶小量O(Δt2)可得：

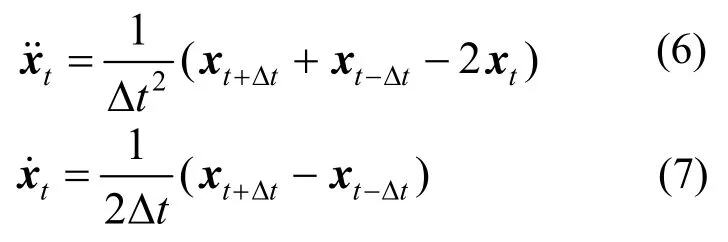
将式(6)和式(7)代入式(3)中，即可得：

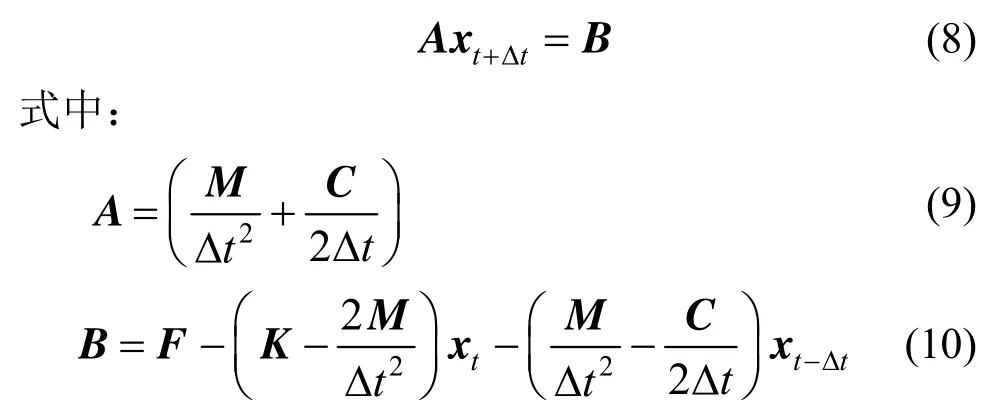
由式(8)、式(9)和式(10)可见，对于显式算法，只要给定初值x0以及x-Δt即可依次求解之后任一时刻的状态量。其中x-Δt可由式(5)舍去高阶小量得到：

式中：x0和为初始条件；可由式(3)求得(t=0)。

蛙跳法在1970年由Hockney[19]提出，在分子动力学领域有广泛应用[20－21]。蛙跳法可以认为是中心差分法的一种变异格式[18]，其与中心差分法的差别在于蛙跳法是在半个时间步上求解速度，如式(12)和式(13)所示。

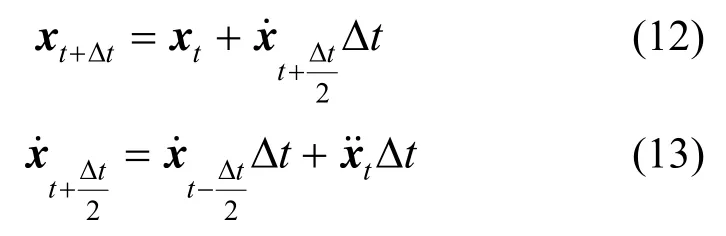
由式(12)与式(13)可见，速度与位移和加速度均未在同一时刻定义，故在将式(12)与式(13)代入运动方程式(3)时，可将代替，获得：

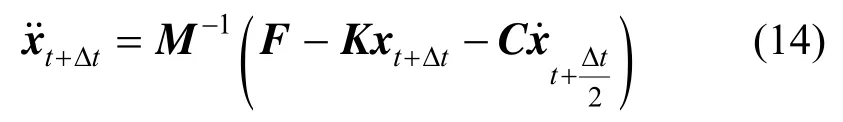
根据式(14)，只需已知x0和即可依次求解之后任意时刻的状态量。在式(14)中将代替，采用了速度近似，会导致算法精度低于传统的中心差分法(只有一阶精度)[13]。此外，使用该方法会造成系统的势能与动能不能在同一时刻定义[22]。为解决上述问题，张书豪[13]提出了一种修正的蛙跳格式显式算法。该方法首先计算xt+Δt：

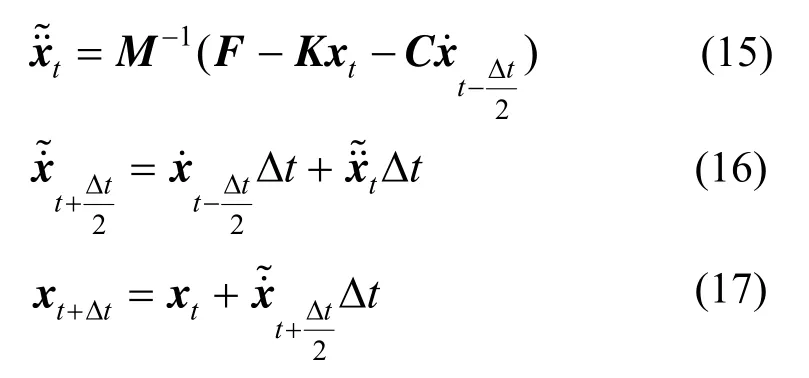
计算得到xt+Δt后，继而利用中心差分法可计算得t时刻的速度与加速度(见式(18)和式(19))，再利用蛙跳法基本步骤式(12)和式(13)，即可得修正后的速度和位移。

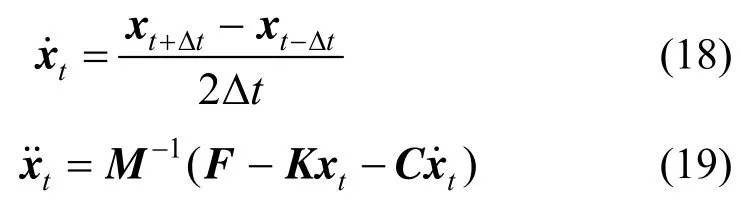
该显式算法对单自由度弹性体系的稳定性条件如式(20)所示[13,18]。其中，显式积分极限步长Δt需满足：

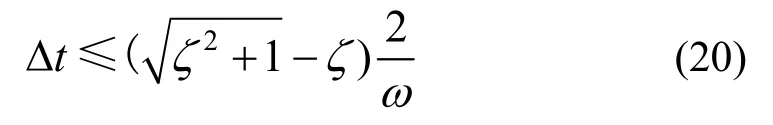
式中：ζ为单自由度体系的阻尼比；ω为单自由度体系的自振频率。

对于有限单元体系，显式积分极限步长Δt应取所有单元极限步长的最小值。单元对应的极限步长与单元的特征长度与单元材料波速有关，梁柱单元以及桁架单元的极限步长为[23]：

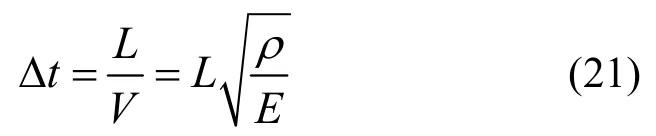
式中：L为梁柱单元长度；V为单元材料波速，取压缩波速；E为材料弹性模量；ρ为单元密度。

与基于蛙跳法的显式算法相配合使用的阻尼格式为质量阻尼与振型阻尼的组合形式，采用这种阻尼形式可以有效消耗大量的计算资源，能够确保方程解耦并且有效抑制不合理的高阶振型的影响[13, 24]。

2 RC框架结构的设计和建模

本文采用文献[25]中6个RC框架结构作为结构对象，包括2个5层结构，2个8层结构，2个10层结构。其中，每一高度结构采用2种地震设防烈度：Ⅶ度(0.1g)和Ⅷ度(0.2g)。为方便以后论述，将上述结构编号为RC5-1、RC5-2、RC8-1、RC8-2、RC10-1、RC10-2。其中，RC后第一个数字代表楼层数，RC后第2个数字中，1代表设防烈度为Ⅶ度(0.1g)，2代表设防烈度为Ⅷ度(0.2g)。所有结构的底层层高为4.4 m，其余层高3.3 m。所有结构均按照设计地震动分组为第1组，场地类型为Ⅱ类(场地特征周期0.35 s)进行设计。结构标准层活荷载为2.0 kN/m2，标准层恒荷载为4.5 kN/m2，屋面恒荷载为7.0 kN/m2，基本雪压取0.30 kN/m2。

结构平面和立面布置如图1所示。各框架梁柱截面配筋如图2所示。其中5层框架的B-1和B-2分别表示边跨梁和中间跨梁，8层框架和10层框架的B-1和B-2分别表示结构下4层或下5层的边跨梁和中间跨梁，B-3表示结构上4层或上5层的梁。

图1 结构平面和立面图 /mmFig.1 Plan view and elevation view of structures

采用OpenSees进行RC框架结构的有限元建模，动力分析时采用基于蛙跳法的显式算法。由于dispBeamColumn单元为基于有限单元刚度法的分布塑性单元，无须单独定义塑性铰，可以很好地用于框架结构梁柱模拟[26－27]。而且张书豪[13]整合于OpenSees的显式算法是基于该单元的，因此本研究中RC梁、柱采用dispBeamColumn单元进行模拟，每一杆件采用3个单元，每个单元采用3个高斯积分点。结构分析中考虑P-Δ效应影响。混凝土采用Concrete01本构模型，钢筋采用Steel02本构模型。材料强度取平均值，材料强度的标准差按文献[26]和文献[28]取值。考虑箍筋约束对混凝土轴向抗压能力的提升，采用Saatcioglu ＆ Razvi模型[29]进行描述。本文以图1中间一榀框架为研究对象进行有限元建模，不考虑楼板的影响。

图2 各框架截面配筋图 /mmFig.2 Section reinforcement diagrams of each frame

3 显式算法与隐式算法的对比分析

选取本文第2节中RC5-1结构作为示例，对比研究显式算法和隐式算法对结构地震反应分析的影响。其中，隐式算法使用瑞利阻尼，显式算法使用质量阻尼与前20阶振型阻尼进行组合。选取El-Centro(1940)地震动记录作为地震输入，分别将地震动的峰值加速度(PGA)调幅至0.1g和3.0g，对RC框架顶点的位移时程及运算耗时进行对比。图3和图4分别给出了PGA=0.1g和PGA=3.0g所对应的RC框架顶点(左上角顶点)位移时程。

由图3和图4中可以看出，在PGA=0.1g时，显式算法与隐式算法的结构响应几乎一致。当PGA=3.0g时，隐式算法由于无法收敛，在6.57 s计算终止，而显式算法无收敛性问题。换言之，采用显式算法可以更加接近结构倒塌状态。

在配备Inter® Core™ i5-7300U CPU @2.60 GHz的计算机上，隐式算法和显式算法的耗时情况如表1所示。从表1可以看出，当PGA=0.1g时，隐式算法因易收敛，而耗时较小，平均单步耗时仅为0.0150 s。当PGA=3.0g时，隐式算法由于存在收敛性的问题，平均单步耗时为0.1766 s，较PGA=0.1g所对应的平均单步耗时增大了约 12倍。对于显式算法，无论PGA大小，平均单步耗时保持稳定，均为0.008 s左右。当PGA= 3.0g时，显式算法平均每秒分析耗时约为隐式 算法的2倍，较PGA=0.1g时(约21倍)，显式算法与隐式算法的总体计算速度的差异有了显著缩小。

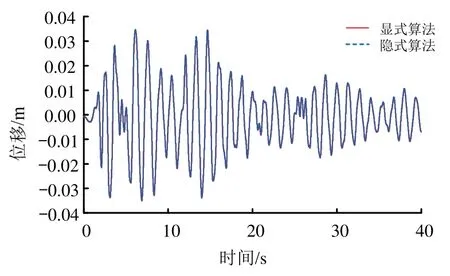
图3 PGA=0.1 g时RC框架顶点位移时程曲线Fig.3 The time history curve of the top displacement of the RC frame at PGA=0.1 g

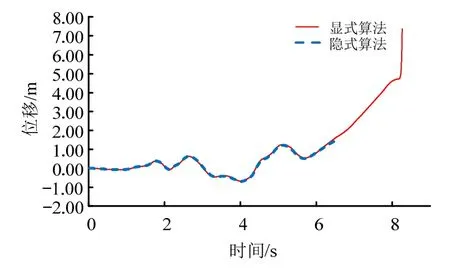
图4 PGA=3.0 g时框架顶点位移时程曲线Fig.4 The time history curve of the top displacement of the RC frame at PGA=3.0 g

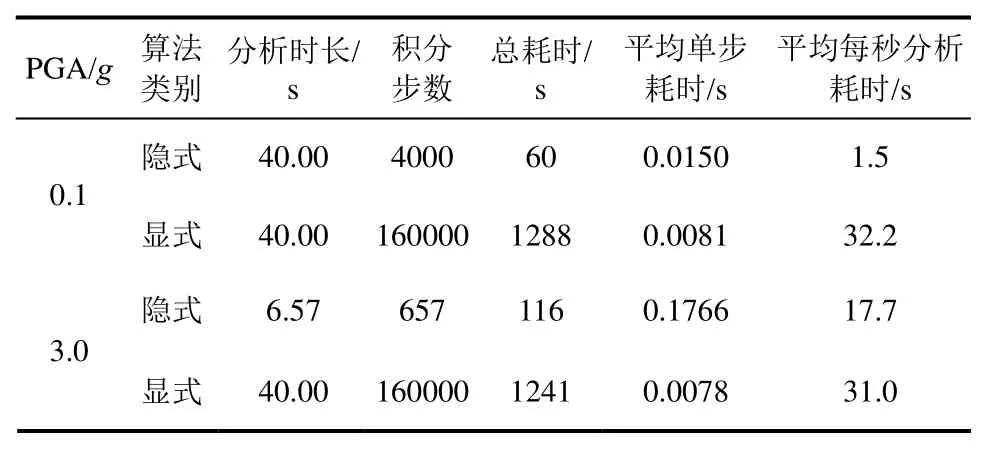
表1 隐式算法和显式算法耗时对比Table 1 A comparison of the time consumption of implicit algorithm and explicit algorithm

4 基于显式算法的结构抗地震倒塌能力分析

4.1 结构倒塌判据

1) 判据1：根据我国《建筑抗震设计规范》[14]，RC框架结构在地震作用下，其薄弱层弹塑性层间位移角不应大于1/50，以防止结构倒塌。为此，本文取结构最大层间位移角θmax=1/50作为结构倒塌判据1。

2) 判据2：美国FEMA 356[15]规定混凝土框架结构防止倒塌(S-5，Collapse Prevention，CP)这一性能水准的层间位移角限值为4%。为此，本文取θmax=4%为结构倒塌判据2。

3) 判据3：根据文献[16]，认为当结构IDA曲线的切线斜率低于初始线弹性阶段斜率的20%时，结构将会发生倒塌，本文将其作为结构倒塌判据3。

4) 判据4：本文以结构变形达到不足以维持“安全使用空间”作为倒塌的物理定义[30]。因此，在进行结构地震反应分析中，可取结构构件竖向倒塌位移超过某一数值作为结构倒塌判据[4,30－31]。本文以结构主要构件竖向倒塌位移超过1 m作为判据4。本文所述的4种判据如图5所示。

图5 4种倒塌判据Fig.5 Four collapse criteria

4.2 IDA分析

选取文献[32]推荐的22条远场地震动进行IDA分析，所选地震动记录的相关信息如表2所示。获得不同结构的IDA曲线，并在IDA曲线上按上述四种结构倒塌判据获得结构倒塌点。仅以RC5-1为例，图6给出了采用判据1～判据3所获得的结构倒塌点。图7给出了采用判据4所获得的结构倒塌点。图8进一步给出了结构RC5-1在表2中第4条地震动作用下，当地震动PGA达到判据4所定义的倒塌强度时，结构θmax和竖向倒塌位移的时程曲线，以及在结构在竖向倒塌位移达1 m时的θmax大小。

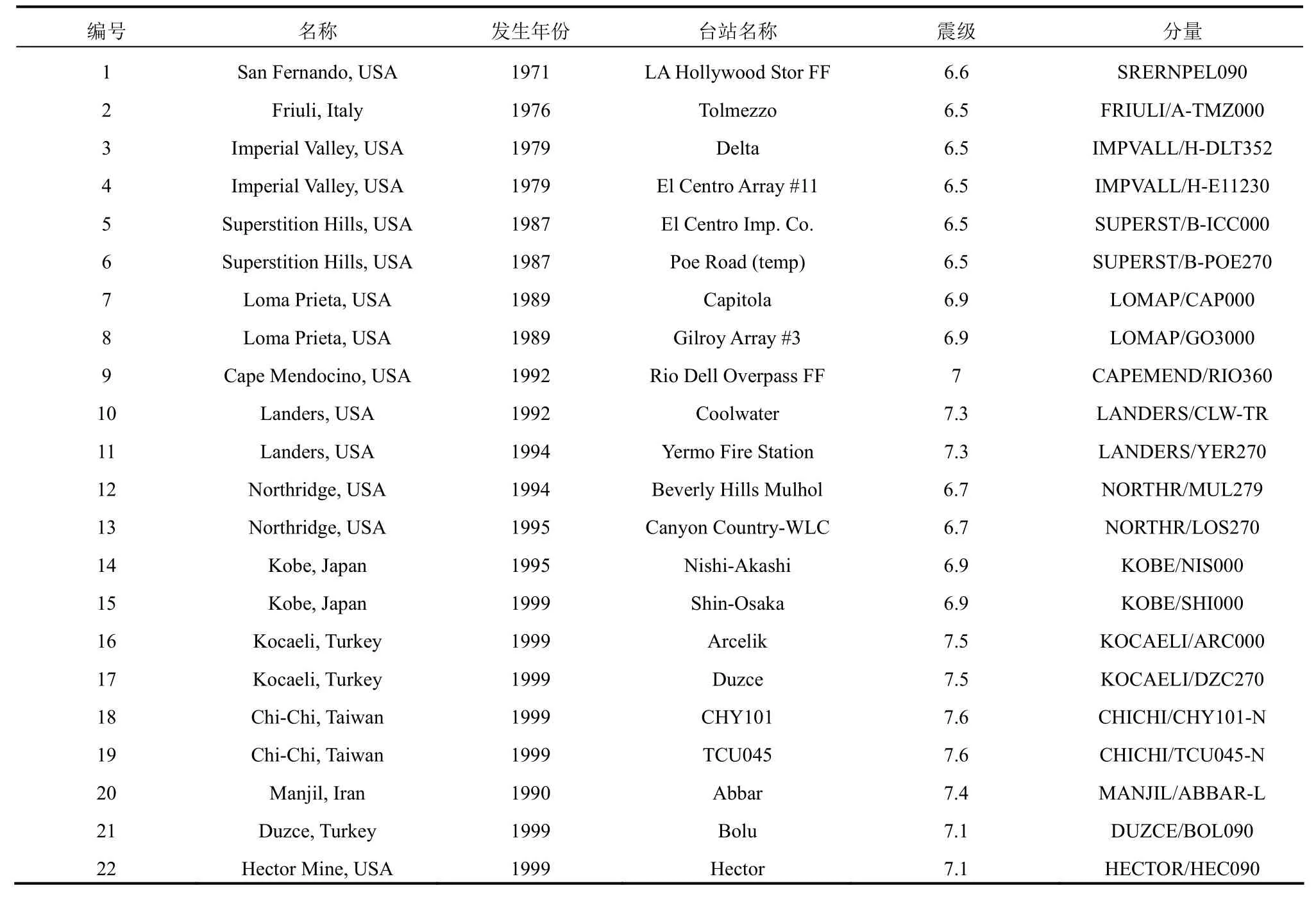
表2 远场地震动记录Table 2 Far-field ground motion records

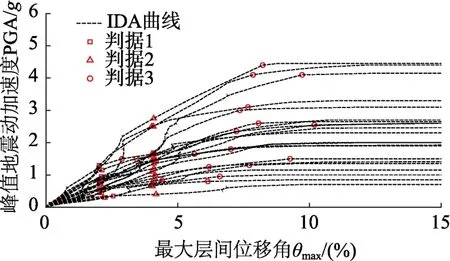
图6 RC5-1框架IDA曲线及前三种倒塌判据的对应点Fig.6 IDA curves of RC5-1 frame and corresponding points of the first three collapse criteria

由图8可见，当结构达到判据4所定义的倒塌状态时，结构的θmax响应在短时间内急剧增加，可认为结构已经崩溃。急剧增加的θmax响应反映了结构在该PGA的地震动作用下已经更为真实地达到了“倒塌”这一极限状态。当地震动PGA达到判据4所定义的倒塌强度时，整个时程的θmax(1015)已不具有实际物理意义，故需要说明的是，为方便展示，图7中所绘倒塌点的状态为达到判据4所定义倒塌强度前一个IDA调幅步所对应θmax和PGA。

图7 RC5-1框架IDA曲线及第四种倒塌判据的对应点Fig.7 IDA curves of RC5-1 frame and corresponding points of the fourth collapse criterion

4.3 地震倒塌易损性分析

基于获得的结构倒塌点，可进一步采用对数正态分布函数进行拟合，获得结构的倒塌易损性曲线，如图9所示。本文获得6个RC算例框架结构对应不同倒塌判据的倒塌易损性曲线，如图10(a)、图10(b)、图10(c)所示。从结果可以看出，判据1明显低估RC框架结构的抗倒塌能力，进一步说明了如判据1这类结构设计规范中提供的供框架结构设计时参考的层间位移角限值只能作为“结构不倒塌”的判据，不能用来作为“结构倒塌”的判据[33]。从易损性曲线可以看出，判据4对RC框架结构的抗倒塌能力的评估要高于判据3，判据2对RC框架结构的抗倒塌能力的评估则低于判据3。

图8 RC5-1结构最大层间位移角时程及最大竖向倒塌位移时程Fig.8 The time histories of the maximum drift ratio and maximum vertical collapse displacement of RC5-1

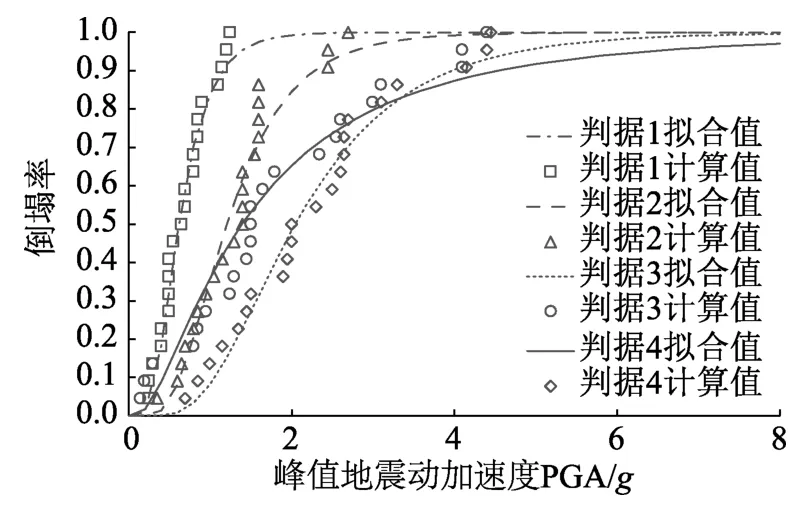
图9 RC5-1 四种倒塌判据易损性曲线对比Fig.9 Comparison of vulnerability curves of four collapse criteria for RC5-1

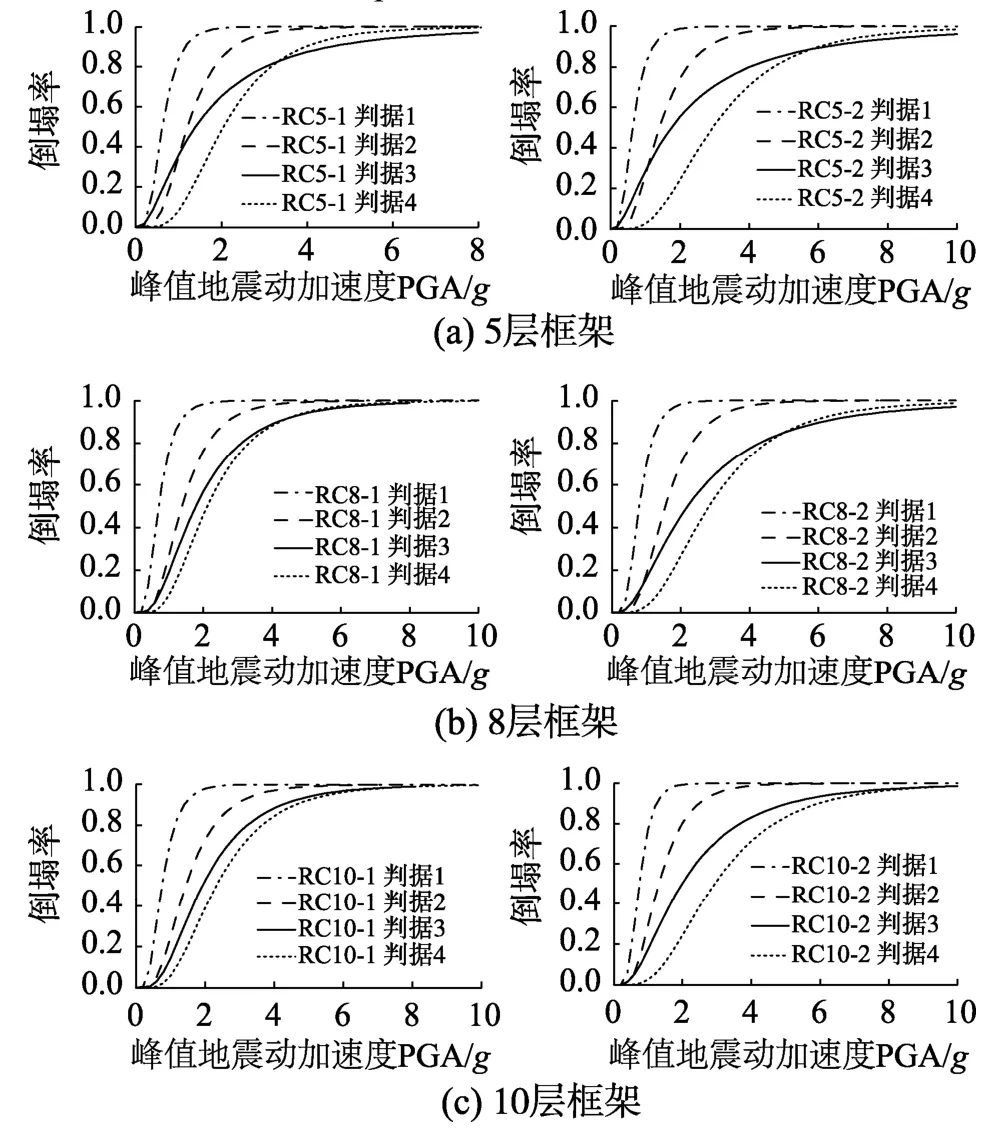
图10 算例结构4种倒塌判据易损性曲线对比Fig.10 Comparison of vulnerability curves of four collapse criteria for case frames

4.4 地震倒塌模式分析

本节以RC5-1为例，对不同判据所对应的结构地震倒塌模式进行了对比。选择表2中第4条地震动为例，当其分别达到不同判据所对应的倒塌强度时(见表3)，所对应的结构倒塌模式，如图11所示。图11中，采用真实结构比例给出了结构在前3种判据所对应的倒塌强度下残余变形模式，以及判据4对应倒塌强度下结构临近倒塌状态的变形模式。图11中还分别给出了对应各判据的顶层侧向变形数值。

由图11可以看出，判据1～判据3所定义的结构倒塌状态的残余变形较小。因此，判据1～判据3显然不能真实地反映结构的倒塌状态。从判据4所定义的结构倒塌状态的结构变形来看，判据4对倒塌的定义显得更加真实，相较于其他3种判据，判据4更好地表现出了结构的倒塌极限状态。

针对判据3和判据4，进一步绘制了结构顶层侧向变形时程，以及不同时刻对应的结构变形模式，如图12所示。

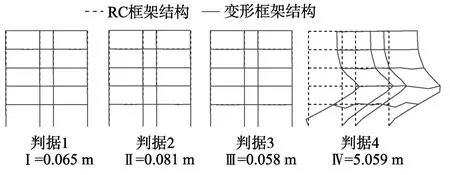
图11 4种判据致倒塌PGA下的位移模式Fig.11 The displacement states under the PGA that causes the collapse corresponding to the four collapse criteria

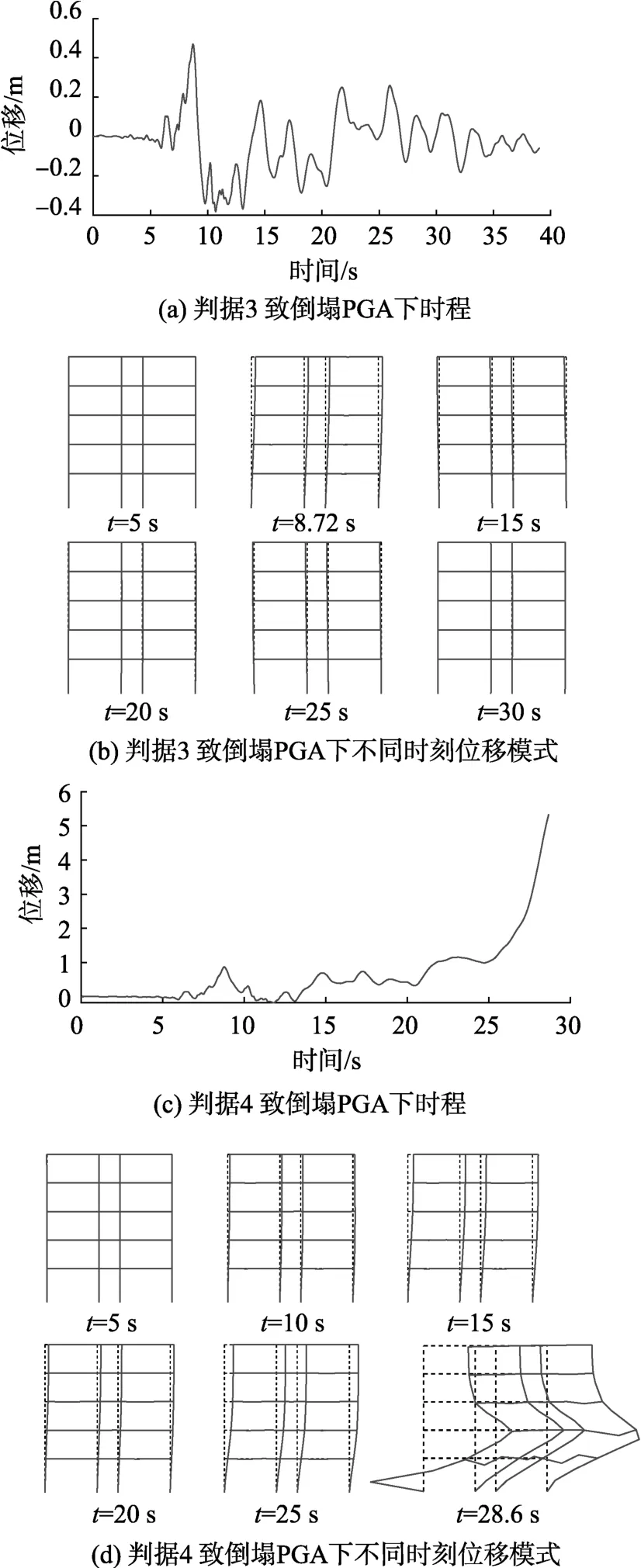
图12 致倒塌PGA下判据3与判据4对应顶层侧向变形时程及不同时刻结构变形模式Fig.12 The time histories of the lateral displacement of the top floor and the displacement states at different times under the PGA that causes the collapse corresponding to collapse criteria 3 and 4

由图12可见，判据3致倒塌PGA作用下结构位移时程响应在整个时程中间一时刻达到最大，但是随后又在波动中有减少趋势。而判据4致倒塌PGA作用下结构位移时程响应在整个时程中呈发散趋势，直至结构崩溃倒塌。

4.5 地震倒塌裕度比分析

地震倒塌裕度比(Collapse Margin Ratio, CMR)也称作结构抗倒塌储备系数，是文献[32]推荐使用的结构抗地震倒塌能力评估指标。本文以PGA为地震动强度指标，罕遇地震对应的CMR为：

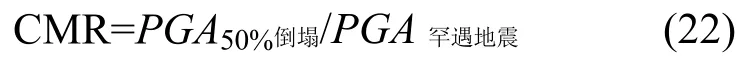
式中：PGA50%倒塌为50%倒塌概率对应的地震动PGA；PGA罕遇地震为参考文献[14]取值的地震动强度。

基于算例框架的地震倒塌易损性，本文进一步计算了6个算例框架对应4种倒塌判据的倒塌裕度比，如表4所示，将不同结构对应不同倒塌判据的倒塌裕度比进行对比，如图13所示。仅以RC5-1为例，相较于判据3而言，判据1对结构的抗倒塌能力低估了约56%，判据2对结构的抗倒塌能力低估了约13%，而判据4对结构的抗倒塌能力高估了约47%。综合6个算例结构的倒塌裕度比结果来看，判据3对应的CMR结果为判据1对应的CMR结果的2.5倍左右，判据2对应的CMR结果为判据1对应CMR结果的2倍左右。这一结果进一步说明了判据1仅适合用作结构设计时的倒塌控制，不适合作为判断结构倒塌的判据[33]。换言之，当结构达到判据1所定义的倒塌状态时，结构仍具有很大的抗倒塌能力冗余度。

判据2相对于判据3而言，其所对应的结构抗倒塌能力低估了13%～34%，且低估程度随着结构层数增加而加深。可见对于RC框架结构，判据2对应的倒塌状态仍有一定的抗倒塌能力冗余度，换言之，FEMA 356[15]规定的混凝土框架结构CP性能水准对应的4%层间位移角限值对于国内RC框架结构而言，作为倒塌判据略显保守。

判据4相较于判据3而言，其所对应的结构的抗倒塌能力结果提高了约20%～70%。这一结果说明判据4所定义的结构倒塌状态比其他判据定义的倒塌状态更为危险。由前文可知，判据4是直接基于倒塌物理定义的，结构在达到判据4所定义的倒塌状态时，迅速完全崩溃并真正达到了完全倒塌。因此，判据4定义的倒塌状态更接近结构的真实倒塌状态，对于RC框架结构，判据4定义的结构抗地震倒塌能力可视为结构抗倒塌能力的上限，也可视为结构的极限抗倒塌承载能力判据。

表4 RC框架结构4种倒塌判据的倒塌裕度比Table 4 CMR of RC frames corresponding to four collapse criteria

图13 4种倒塌判据下RC框架结构CMR比较Fig.13 Comparison of CMR of RC frame structures under four collapse criteria

5 结论

本文针对不同层数、不同设防烈度的6个RC框架结构，基于改进蛙跳法的显式算法，进行了RC框架结构的抗地震倒塌能力分析，获得了结构的倒塌易损性曲线和倒塌裕度比，得到如下结论：

(1) 显式算法与隐式算法在结构非线性发展程度不强时，分析结果基本完全吻合。与隐式算法相比，显式算法非线性分析的收敛性更好，也更易于模拟结构在倒塌状态附近的非线性行为。

(2) 判据1和判据2对结构抗地震倒塌能力的评估结果较为保守，用其来评估结构抗地震倒塌能力，结构仍有较大抗倒塌能力冗余度。与判据3对应的结果相比，判据4对应的结构倒塌裕度比要高20%～70%。

(3) 判据4基于结构倒塌的物理意义，在判据4所对应的结构倒塌状态，结构在地震动作用下变形急剧增大乃至崩溃达到完全倒塌。相较于前3种倒塌判据，判据4能更好地体现结构倒塌状态的真实非线性行为。由于显式算法较强的非线性分析能力，因此其可以不受制于收敛性问题，而可以方便利用判据4来进行倒塌能力的评估，有利于结构真实抗倒塌能力的评估。