小问题2020-1

《小问题》栏目欢迎来稿出题(请自拟题目或注明题目来源), 题目及解答请寄《力学与实践》编辑部, 采用后将致薄酬.

2020-1 圆环半径为r，质量为m，以向前的水平速度和相应于回滚方向的角速度与水平地面接触。接触时，圆环与其移动速度在同一个铅垂平面内。圆环和地面的滑动摩擦系数为f，滚动摩阻不计。问：

(1) 在什么条件下圆环会回滚？

(2) 在何时何处开始作纯滚动，角速度是多少？

(3) 在什么条件下，回滚的圆环正好在着地时开始作纯滚动？

(供稿：薛聿泷)

《小问题》栏目开展有奖竟答啦！2020 年4 月10 日前将题目解答发送到lxsj@cstam.org.cn，解答正确者即可免费获赠《力学与实践》2020年第1期期刊1本(来信时请注明邮寄地址)。期待您的参与！

*《小问题》2019-5解答*

问题：如图1所示，两个小球构成3自由度的机构，铰链O 可以绕竖直轴z 轴自由转动，直角弯杆与铰链铰接，可绕过O 点的x 轴自由转动，小球A 固定在弯杆的末端，小球B 由直杆约束绕O′A轴自由转动。铰链的质量和尺寸均忽略不计，各杆均为轻杆，直杆和直角弯杆两段的长度均为a，两小球质量均为m。

(1)在图1所示位置，小球A的坐标为(0,a,-a)，小球B 的坐标为(a,a,-a)，求系统由静止释放时，施加给系统的约束反力；

(2)试求此系统的稳定平衡位置；

(3)试求此系统在稳定平衡位置附近微幅摆动的线性微分方程。

(供稿：宝音贺西，清华大学航天航空学院)

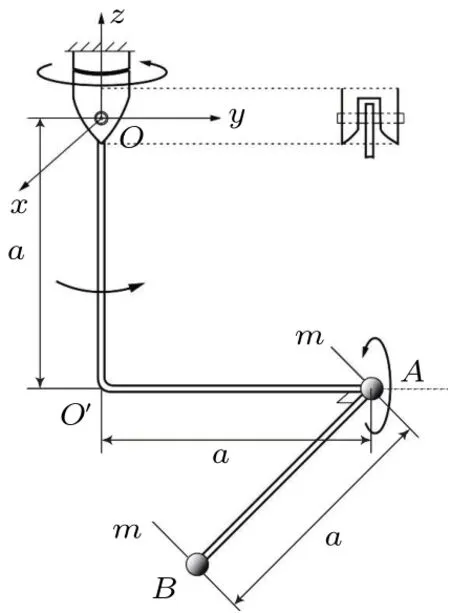
图1

解答：(1)如题图所示的初始状态建立惯性坐标系，则在此惯性坐标系中，小球A 的位置由绕z 轴和x轴的转角α，β，小球B 的位置由绕O′A 的转角γ 描述。建立随直角弯杆转动的坐标系OXY Z，此坐标系与惯性坐标系之间的转换矩阵为A。

设初始时悬挂点处的约束力为NO= NOxi+NOyj + NOzk，约束力矩为MO= Mj，其中i，j，k 为惯性坐标系x，y，z 方向的单位矢量。设AB 轻杆对小球作用力为N，由轻杆约束条件可得，初始时此作用力在z 方向的分量Nz= 0。设小球A 的位置矢量为rA，小球B 的位置矢量为rB，在OXY Z 坐标系以列阵表示为A = [0,a,-a]T、B= [a cos γ,a,-a-a sin γ]T，进一步利用矩阵A即得到惯性系中表达式。初始时，对小球A和B 位置矢量求导可得

则由小球A对O 点的角动量定理得

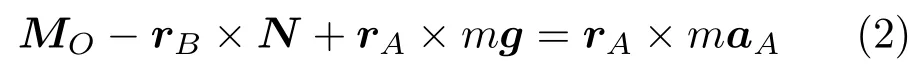
对小球A列牛顿第二定律得

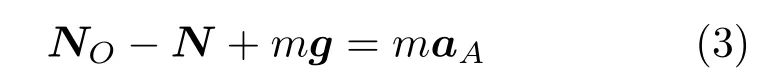
对小球B 列牛顿第二定律得

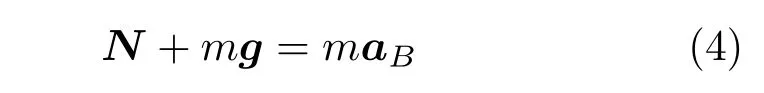
联立式(1)∼式(4)，可解得

(2)由小球A 和B 在惯性坐标系中的位置矢量得到二者z 方向的位置，即

则系统的势能为

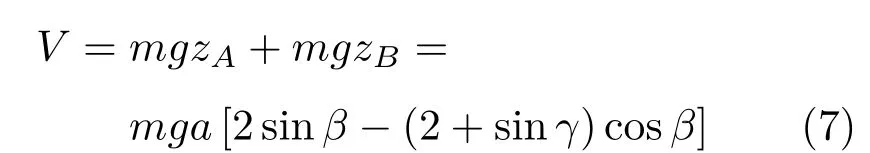
系统的平衡位置为势能的极值点，求导得

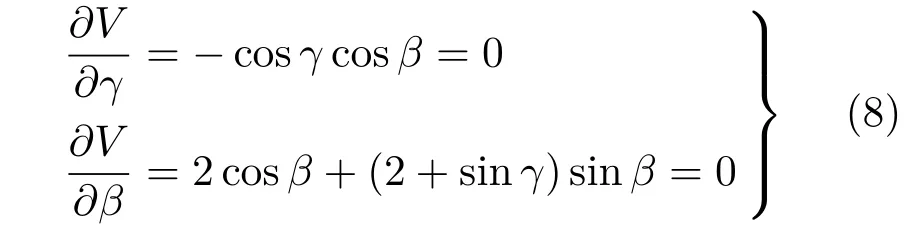
解得平衡点(α取任意值)依次为

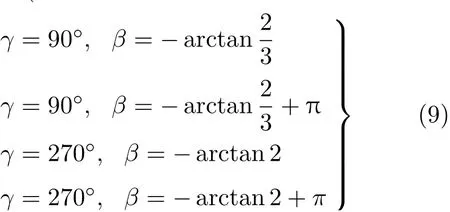
进一步由势能对γ和β的Hessian矩阵正定性判定稳定平衡位置为(3)由小球A和B的速度在OXY Z坐标系下的列阵表示为

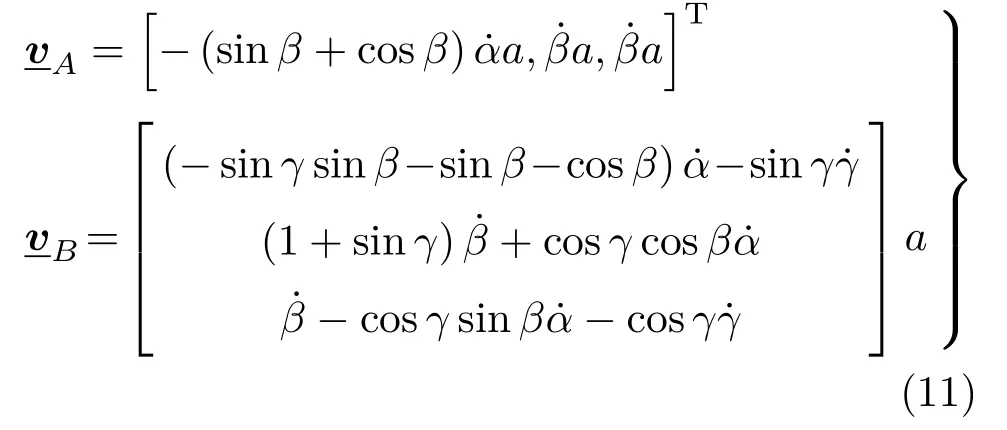
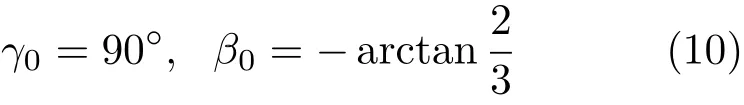
因此系统的动能为

系统的拉格朗日函数为

根据第二类拉格朗日方程，且选取广义坐标q1=α，q2=β-β0，q3=γ-γ0，系统做微幅摆动时广义速度均为小量，解得

进一步整理得线性微分方程为