再谈无人自行车的自稳定性

刘延柱

(上海交通大学工程力学系，上海200240)

2016 年Google 宣布已造出能自动行驶的无人自行车，引起不小的轰动。但随后声称只是个愚人节玩笑。此前有报导称，2011 年荷兰Delft 大学的Kooijman 曾制造出无人自行车。但他的实验对象是特殊设计的小车，与常规的自行车截然不同[1]。2015年，清华大学自动化系学生在赵明国老师指导下造出了真正的自平衡无人自行车，在全国虚拟仪器大赛中获得唯一的特等奖。2017 年在美国奥斯汀的NI WEEK 2017 大会中展示，入围NI Engineering Impact Awards，受到科技界的极大关注[2]。

关于自行车稳定性问题的讨论已延续了两百多年。早在19 世纪提出的离心力效应至今仍是自行车稳定性的经典解释。车轮的陀螺效应有助于自行车的稳定，但1971 年英国人Jones[3]的实验证实陀螺效应的影响极其微弱，其作用远不如与前轮接触点有关的脚轮效应。1982 年，英国人Lowell 和McKell建立的自行车数学模型考虑了离心力效应、陀螺效应和脚轮效应等所有因素，还增加了前叉转角随车身侧向倾斜角变化的简单控制规律。基于此模型导出的特征根存在正实部，数值计算也得出振幅不断增大的不稳定振荡的运动轨迹。表明即使考虑所有稳定因素且增加对前叉的自动控制，也不能使自行车保持稳定[4-5]。

如上所述，自稳定无人自行车已在近期内成功实现。上述不稳定性的分析结论已被实践彻底否定。实际上凭常识也能判断，自行车能否稳定的重要因素是驾车人的控制技巧。关键在于，控制规律是否真正体现人的驾车技术。本文仍采用相同的数学模型，仅对控制规律作一些修改，对自行车自稳定性问题继续做些探讨。

将自行车视为由车架、前叉和前后轮组成的刚体系。设O1和O2为后轮和前轮与地面的接触点，以O1为原点建立参考坐标系(O1-xyz)，其中x轴沿O1O2，y轴为垂直轴。设绕轴逆时针转过θ角后的位置为(O1-x1y1z1)，(x1,y1)为车架平面。设O1与O2的距离为a，质心Oc的直立高度为h，在x轴上的投影与O1的距离为b。设车架随O1点以速度v沿x轴匀速平动(图1)，前轮偏角ψ的出现使自行车转为曲线运动(图2)。图中O为曲率中心，R=a/ψ为曲率半径。近似将车体的全部质量m集中在Oc点，仅保留θ和φ的一次项，列写车体在重力mg和离心力mv2/R作用下绕水平轴x转动的动力学方程。引入参数α=bv/ha,β=v2/ga,γ=g/h，写作

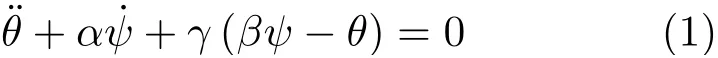
列写前叉与前轮的组合件绕转轴转动的动力学方程时，为简化数学推导，仍按文献[4]中的假定将倾斜的前叉转轴y*拉直，使与O1O2正交。将(O1-x1y1z1)的原点移至O2，绕y1轴顺时针转过ψ角后的位置为(O2-x2y2z2)。其中y2轴平行于前叉转轴y*，x2轴沿轮缘在O2点处的切线，(x2,y2)为前叉的对称平面。考虑地面在O1和O2处对车体和前叉施加沿z1和z2轴的摩擦力与离心力平衡。且考虑前叉转轴y*与地面的交点O*与O2点不重合的距离Δ形成的脚轮效应(图3)。设车架与前叉之间存在绕转轴y*的阻尼力矩

其中C为黏性摩擦系数。考虑控制系统的作用，将陀螺仪量测到的车体侧向倾斜角θ和角速度˙θ的信息输入电机，产生绕前叉转轴的控制力矩Mcy，控制规律为

其中Jy为前叉连同前轮绕转轴y*的惯量矩。引入参数μ=mgbΔ/(Jya)，c=C/Jy，列出前叉的动力学方程

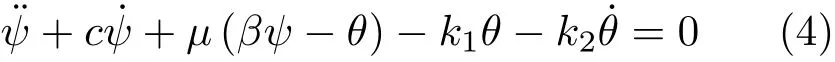
方程(1)和(4)的具体推导过程可参阅文献[4-5]。仅对文献中的动力学方程略去影响微弱的陀螺力矩，增加了阻尼力矩Mdy和控制力矩Mcy。

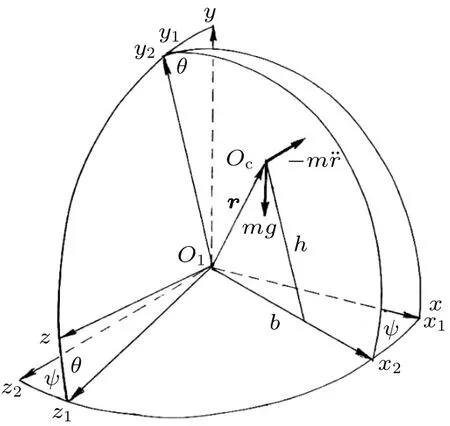
图1 参考坐标系

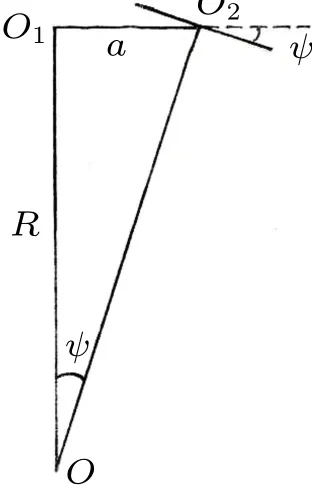
图2 运动轨迹的曲率半径

图3 前叉转轴与前轮触地点

方程组(1), (4)的特征方程为

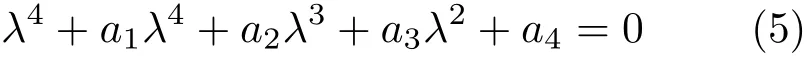
其中的系数定义为

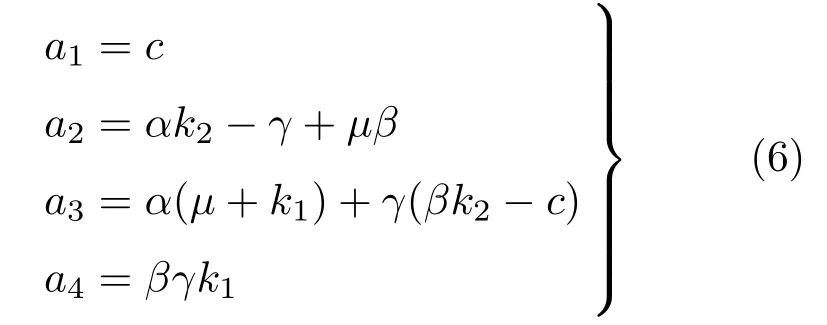
利用Hurwitz 判据判断线性系统的稳定性，所有系数为正值是方程组(1)和(4)零解渐近稳定的必要条件。此条件要求控制系数k1和k2满足

如a1a2-a3＞0条件也满足，即

则渐近稳定性充分成立。在c/= 0，k2/= 0 条件下，借助控制系数k1和k2的调整可使上述诸条件均得到满足。从而证实无人自行车直立行驶状态存在渐进稳定性的可能性。

以上分析表明，利用对前叉的自动控制，实现无人自行车直立行驶的稳定性在理论上并无问题。但必须考虑前叉转轴的阻尼因素，且控制规律中除车体倾斜的角度信息以外，还必须计入角速度信息。Lowell 和McKell 的论文未考虑上述因素，才导致不稳定的计算结果[4-5]。

直立稳定性只是无人自行车的关键问题之一。要真正实现无人自行车，还必须攻克转弯、过障碍、跟踪等许多技术难关。清华大学的老师和学生们不畏艰难，坚持不懈，终于造出了无人驾驶自行车，震惊了世界，也开启了自行车发展史的新阶段。