刚架稳定分析

王开福

(南京航空航天大学航空学院，南京210016)

问题刚架如图1 所示，垂直杆AB和CD的弯曲刚度均为EI，长度均为l，水平杆BC的弯曲刚度为E1I1，长度为l1，A和D处固定铰支，B和C处刚性连接。已知刚架B和C处分别受垂直向下的集中力F作用，假设AB和CD均为细长压杆，试求刚架临界载荷Fcr。

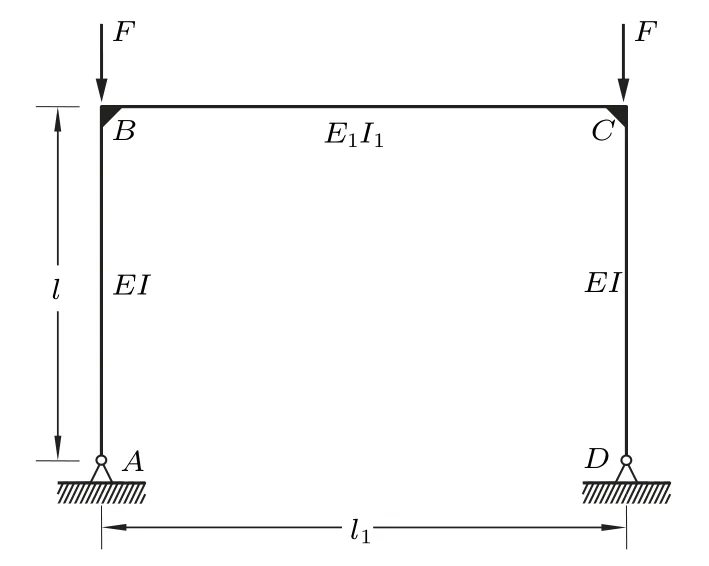
图1

解答与本题相同或相似的刚架稳定问题在材料力学参考书中常会出现，然而这些参考书给出的解答通常不够完善，甚至还有错误，尤其是没有得到最终结果。

事实上，本题是非常典型的压杆稳定问题，正确求解本题对学生深刻理解压杆稳定概念和熟练掌握压杆稳定计算具有重要意义。为此，本文将对刚架稳定问题进行深入探讨和详细分析。

假设刚架在临界载荷作用下处于微弯状态而平衡，如图2所示。根据静力平衡条件，得

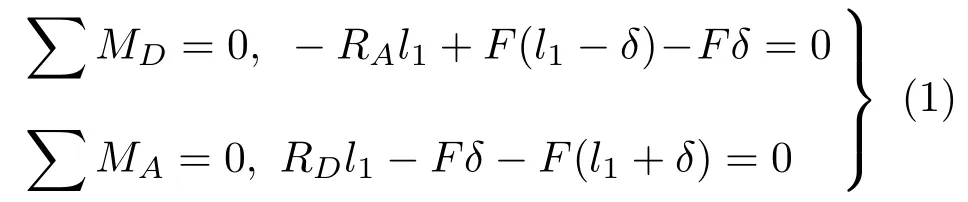
式中，δ为节点B和C的水平位移。通过求解上述方程，得到刚架在A和D处的反力

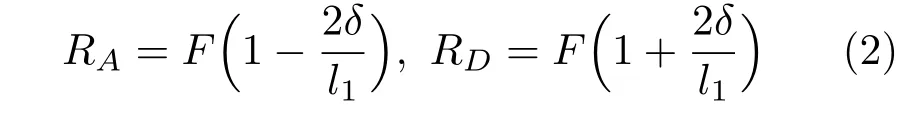
考虑垂直杆AB(垂直杆CD可作相同分析)，设截面x处挠度为w，如图2 所示，则截面x处弯矩可表示为[1-2]

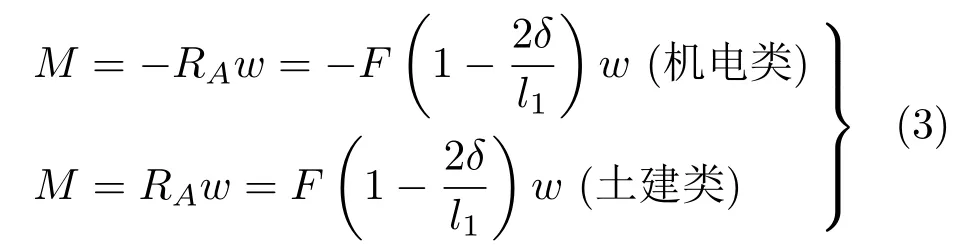
上式分别代入相应挠曲线近似微分方程[1-2]

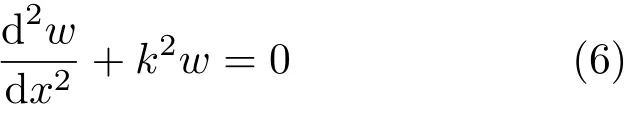
式(6)通解可写为

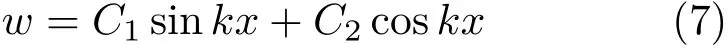
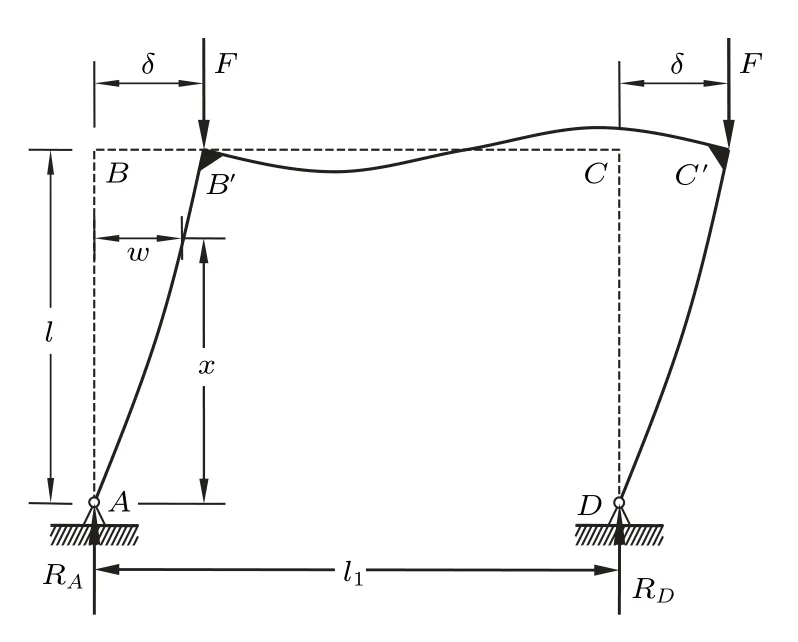
图2

式中，C1和C2为常数，可通过边界条件确定。当x= 0 时，有w|x=0= 0，由此得C2= 0；当x=l时，有w|x=l=-δ，由此得C1=-δ/(sinkl)。因此式(7)可重写为

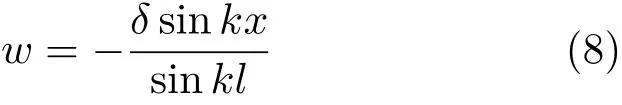
刚架在临界载荷作用下处于微弯状态而平衡，则水平杆BC将发生弯曲变形，如图3 所示，变形后的BC由B′C′表示，可等效为简支梁两端分别受集中力偶RAδ=F(1-2δ/l1)δ≈Fδ和RDδ=F(1+2δ/l1)δ≈Fδ作用。利用叠加原理，水平杆BC在节点B处转角为

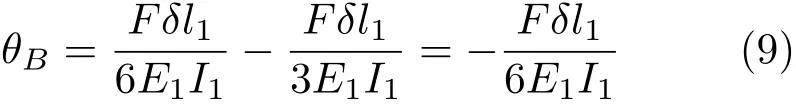
式中，负号表示顺时针。

由式(8)可知，垂直杆AB在节点B处转角等于

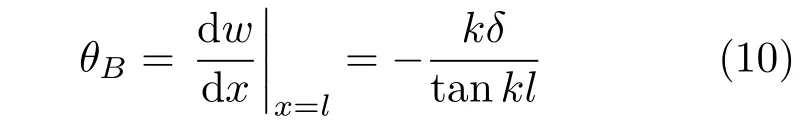
由于垂直杆AB和水平杆BC在节点B转角相等，故有

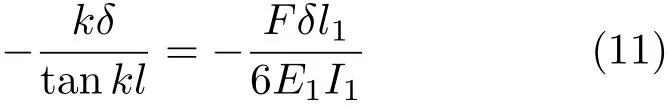
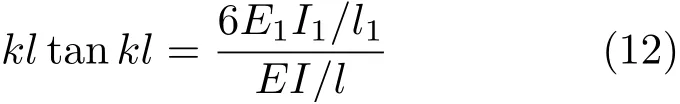
求解上述方程，得β∼α曲线如图4所示。

通过β∼α曲线，可确定与α对应的β，然后利用为长度因数 即可确定临界载荷Fcr。典型情况的临界载荷分别为：

(1)α→∞，即有β= 1.57，即μ=2.0，则临界载荷该式即为一端固定、一端自由细长压杆的欧拉公式。

(2)α= 10，即有β= 1.55，即μ= 2.0，则临界载荷该式表明，当

(3)α= 1，即有β= 1.34，即μ= 2.3，则临界载荷F该式表明，临界载荷有所降低，承载能力降低25%。

(4)α= 0.1，即有β= 0.705，

即μ= 4.5，则临界载荷该式表明，临界载荷显著降低，承载能力降低80%。

(5)α→0，即有β→0，即μ→∞，则临界载荷Fcr→0。该式表明，刚架已不能承载。