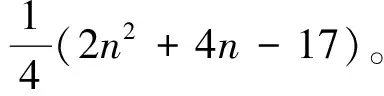具有第三小边平均Wiener指标的单圈图

苏晓海

(陕西理工大学 数学与计算机科学学院， 陕西 汉中 723000)

长期以来，图论的研究中关于分子拓扑指标研究始终是一个热点问题[1-5]。图的边平均Wiener指标就是一个重要的分子拓扑指标。图的边平均Wiener指标在计算机系统、物理学领域、信息系统、交通系统等方面都有比较广泛的应用。它与化学分子的许多物理性质和化学性质密切相关，比如分子的熔点、沸点等。近些年来图的边平均Wiener指标引起了许多研究者的注意，人们对它进行了广泛深入的研究，且得到了一些较好的重要结果[5-9]。

本文涉及的图都是无向的简单连通图。用V(G)和E(G)分别表示图G的顶点集和边集，|V(G)|表示图G的顶点数(阶数)，|E(G)|表示图G的边数。对于一个图G，把|E(G)|-|V(G)|+1称为图G的圈数，记为λ=|E(G)|-|V(G)|+1。当λ=1时图G称为单圈图。图G中度为1的顶点称为悬挂点，与悬挂点关联的边称为悬挂边。n阶树如果只有两个悬挂点则称为路；n阶树如果有n-1条悬挂边则称为星，其中所有悬挂边的公共顶点称为星的中心。设u和v是图G的任意两个顶点，把连接u和v的最短路的边的数目称为这两个顶点u和v之间的距离，记为d(u,v)。图G中所有无序顶点对的距离的总和称为图G的Wiener指标，即

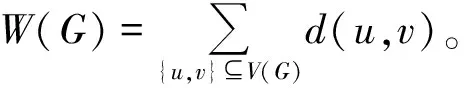
设f=uv、g=xy是图G的两条边，把边f和g的四对不同顶点对u与x、u与y、v与x、v与y之间的距离之和的1/4称为边f和g的平均距离，记作D′(f，g)，即

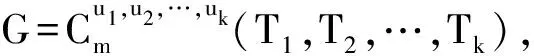
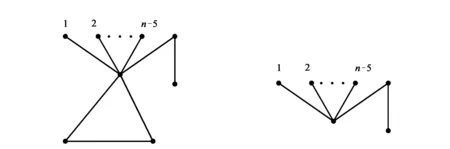
(a) C3(Sn-3,1) (b) Sn-3,1 图1 C3(Sn-3,1)和Sn-3,1

本文研究单圈图的具有第三小边平均Wiener指标的图的特征，并给出第三小边平均Wiener指标的计算公式。为此先介绍下面的几个引理。

1 引 理

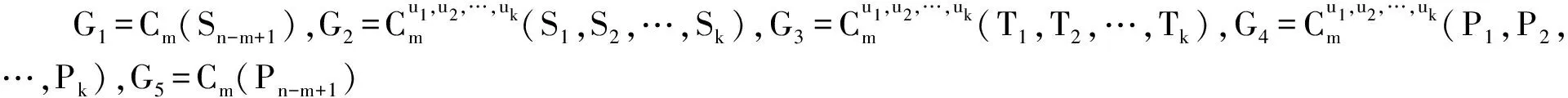
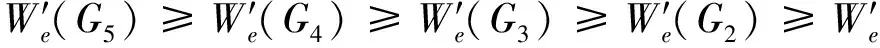
其中|Si|=|Ti|=|Pi|，且Si、Ti、Pi的根均为ui，i=1,2,…,k。

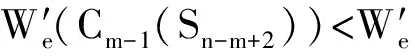
2 主要结果

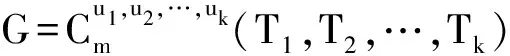
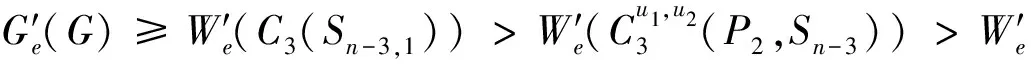
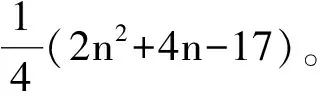
证明(ⅰ) 按定义直接计算得到

从而

所以

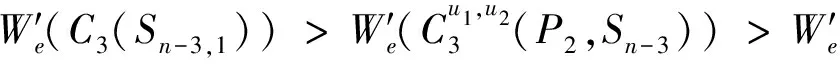
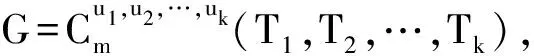
分两种情形来证明。

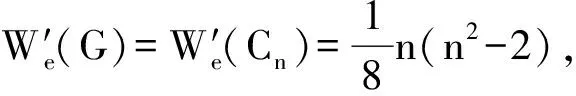
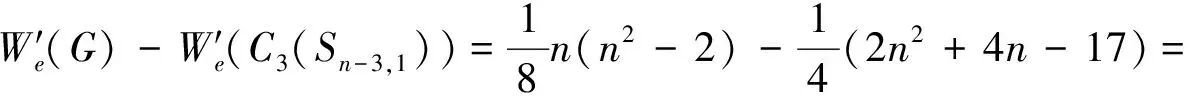
所以

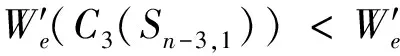
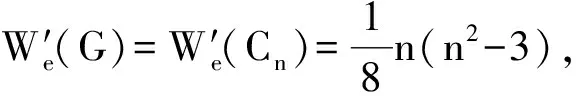
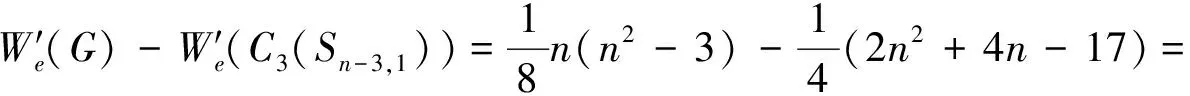
所以

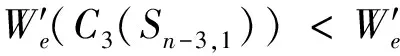
情形二当k≥1时，由引理1和引理2可知，

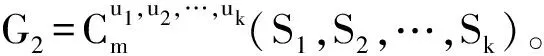
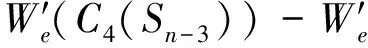
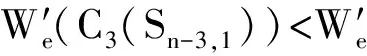
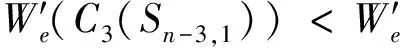
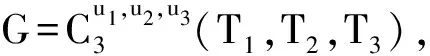
由于n>8，m=3，故k取值只可能是1、2或3。

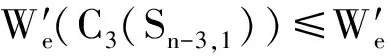
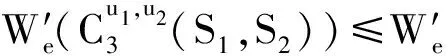
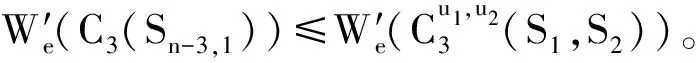
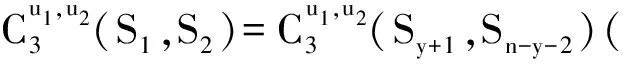
按定义直接计算，得

因为

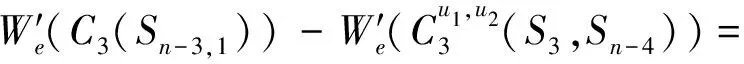
所以

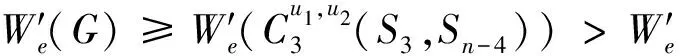
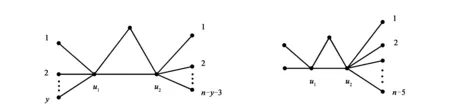
图和

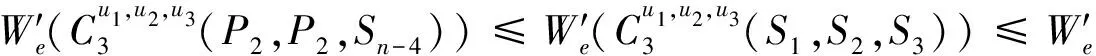
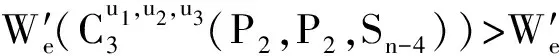
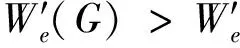
综上讨论，可得，当n>8时，

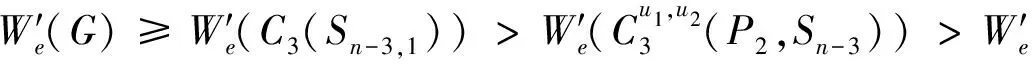
等号成立当且仅当G≅C3(Sn-3,1)。所以当n>8时具有第三小边平均Wiener指标的单圈图是C3(Sn-3,1)。定理得证。

3 结 论