内置大质量管道对综合管廊地震响应的影响
2020-03-16马宏伟胡天羽李宇华
马宏伟, 胡天羽, 郭 鸿, 李宇华
(1.安徽理工大学 土木建筑学院, 安徽 淮南 232001;2.陕西理工大学 土木工程与建筑学院, 陕西 汉中 723000)
我国综合管廊建设的历史最早可追溯到1958年,但发展十分缓慢[1]。2015年中央城市工作会议召开后,国内综合管廊迎来了建设高潮,建设规模达到了每年2000 km左右。同时,作为全球地震最频繁的国家之一,我国工程结构面临的震害威胁特别突出,开展综合管廊的地震响应研究具有重要的工程意义。
人类对地下结构的抗震研究起步较晚,1995年日本阪神大地震引起地铁车站等地下结构严重破坏后,地下结构的震害严重性才引起业内的重视。过去的20多年,国内外研究者围绕地下结构的抗震问题开展了一系列研究,并形成了原型观测、试验模拟、理论计算、数值分析等研究方法。叶飞等[2]在四川省雅安市芦山地震后运用原型观测方法进行了灾区供水系统的震害调查;Baziar等[3]采用试验模拟手段完成了隧道的振动台缩尺试验;马宏伟等[4-6]采用波函数展开法开展了输水隧道地震响应的系列理论计算。
由于原型观测、试验模拟、理论计算等方法存在一定的局限性,目前采用上述方法进行综合管廊地震响应研究的报道并不多见,既有研究工作多采用数值分析方法展开。杨剑等[7]使用基于有限差分法的FLAC软件对地震作用引起的液化土中综合管廊地震响应进行了模拟分析;周晓洁等[8]采用ABAQUS有限单元法软件研究了地震波入射角度、土层波速结构及覆盖层厚度对综合管廊地震响应的影响;杨仕升等[9]则针对综合管廊节点的抗震问题进行了二维有限元模拟分析;Milind[10]分析了场地运动特性对管廊地震响应的影响。此外,蒋录珍[11]、闫钰丰[12]、郭恩栋[13]等都采用有限单元法软件针对具体综合管廊工程开展结构地震响应分析,得到了一系列对工程建设十分有益的成果。然而,上述研究工作均围绕管廊结构自身在地震作用下的动力响应问题展开,未能考虑到内部管道对结构响应的影响。实际上,大直径给排水管道在运营过程中整体质量很大,地震发生时管道惯性力通过支墩传递至管廊结构,可造成结构动力响应的变化,严重威胁管廊结构的抗震安全性。
综上分析,本文采用有限单元法数值分析的方法研究内置大质量管道对综合管廊地震响应的影响规律,旨在为地下结构灾变机理的揭示和综合管廊的抗震设防提供参考。
1 综合管廊动力有限元分析模型的建立
本文研究对象为安徽省铜陵市某在建综合管廊工程,场地内土层由上至下依次为杂填土、粘土、中风化岩石、强风化岩石,场地类别为二类场地,各土层参数如表1所示。管廊结构采用C35防水混凝土现浇而成,各构件厚度均为0.5 m,埋深为1.5 m,断面为净空36 m2的L形三仓形式,各分仓依次定义为A1仓、A2仓和A3仓,管廊结构断面形式及尺寸如图1所示。模型中各材料均为完全弹塑性材料,其本构关系采用DP(Drucker-Prager)准则。

表1 土层物理力学参数
为便于问题描述,在管廊各构件端点及跨中位置设置30个观测点,观测点分布情况如图2所示。
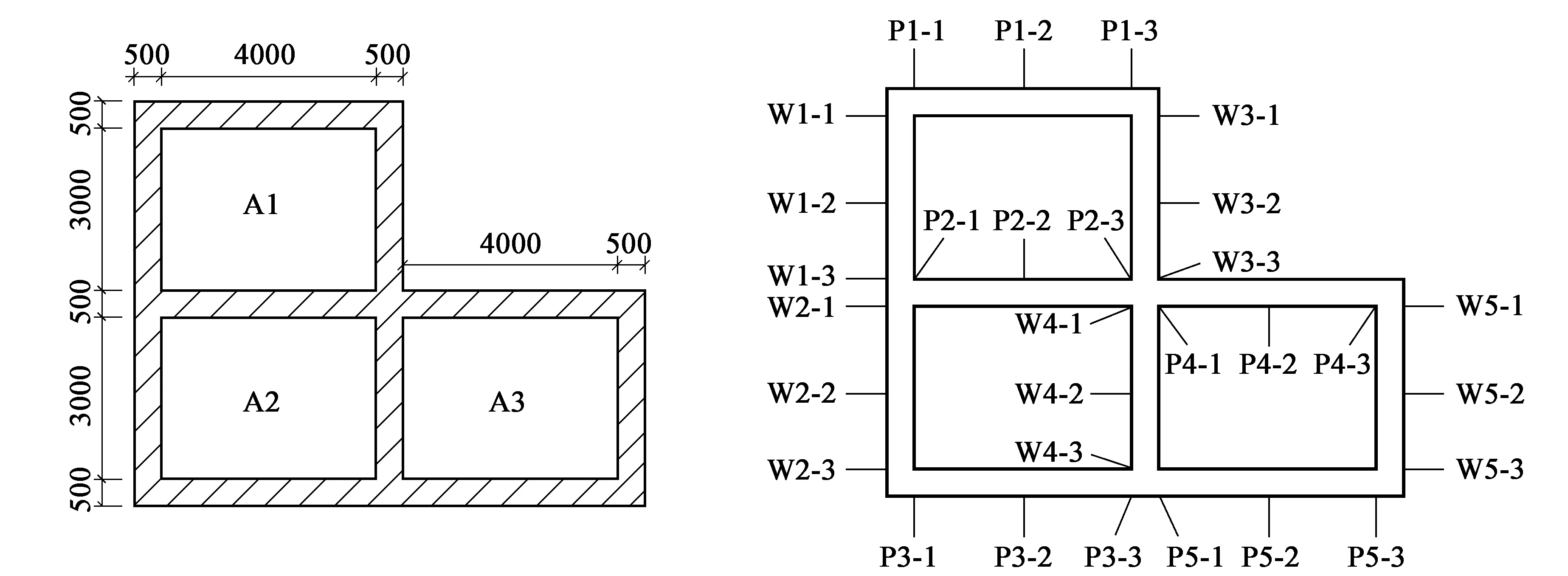
图1 综合管廊横断面图 图2 响应分析观测点分布图
管廊内布设DN1200供水管道,管材为Q345钢,壁厚14 mm、外径1230 mm,采用间距6 m、沿管轴方向长度1 m的钢筋混凝土支墩支承。研究中不考虑管道内水体的复杂震荡效应,仅考虑管道与水体质量对结构响应的影响,故将相邻支墩间的管道与水体质量集中至支墩位置,并采用等效密度为ρEQ的圆柱体代替管道及内部水体,经计算得到完全充水的最不利工况下支墩所在断面处圆柱体的等效密度ρEQ=9311 kg/m3。
综合管廊属于线形结构,满足平面应变问题条件,因此本文采用平面有限元法进行分析。
1.1 研究工况
为对比分析管道对结构地震响应的影响,考虑4种不同工况:管廊内不设置管道为工况一;管道设置于A1仓为工况二;管道设置于A2仓为工况三;管道设置于A3仓为工况四。在有限元软件ANSYS中建立工况一分析模型,模型尺寸54 m×30 m,划分网格后形成单元6360个,节点19 416个,工况一有限元网格划分结果如图3所示,其他工况下的网格划分与工况一类似,此处不再赘述。工况二中管道设置在A1仓中央,具体位置及尺寸如图4所示。工况三与工况四中管道在对应分仓内的位置与工况二相同。
本文研究中不考虑管道支墩刚度对结构地震响应影响这一复杂问题,故在模型建立中在支墩位置设置了等效集中质量块来反映管道对结构的影响。由于周围土体与结构在地震作用下满足接触面处的位移连续与应力连续条件,土-结构接触面采用共节点方式处理。

图3 工况一有限元网格划分图
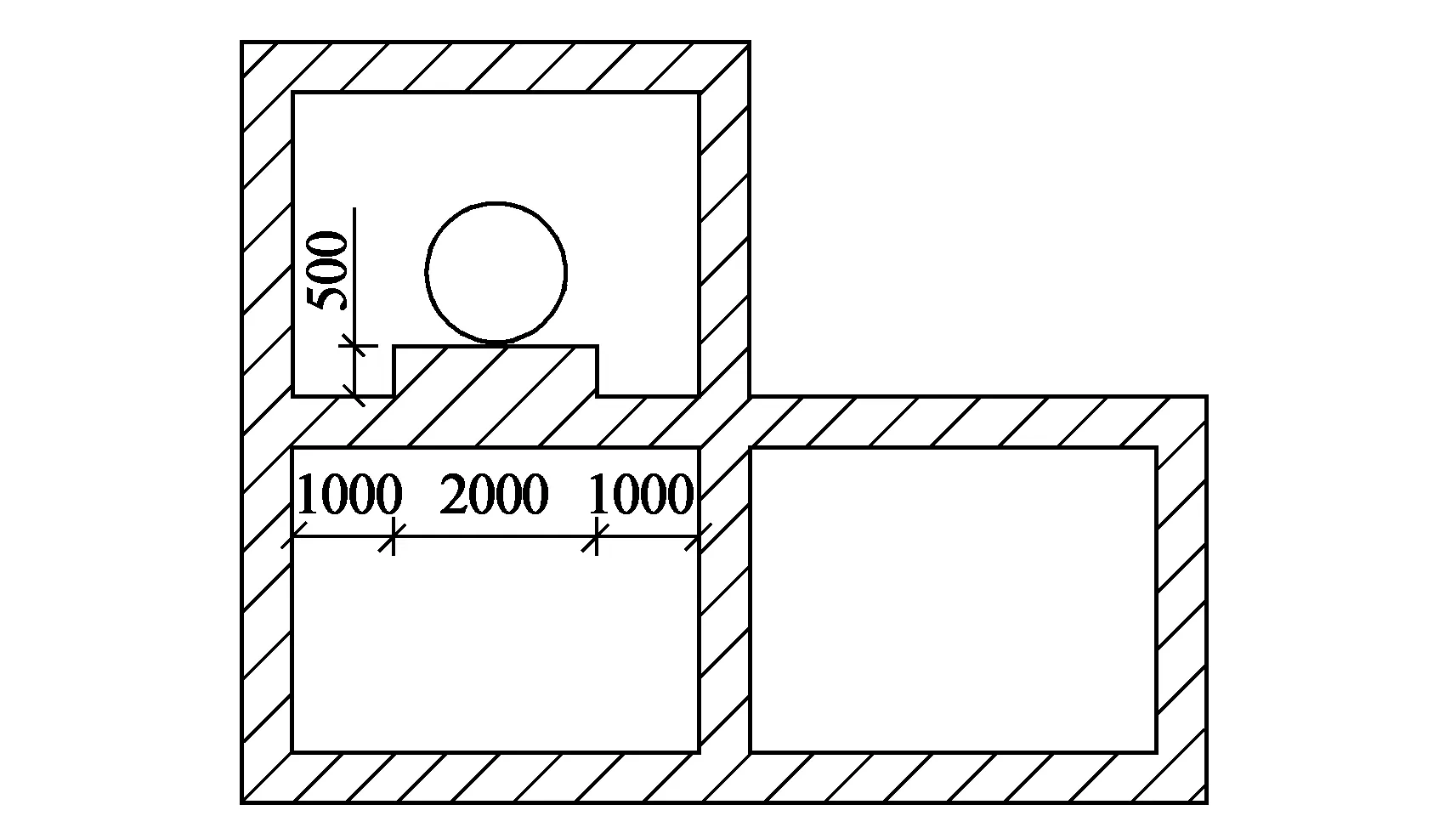
图4 工况二管道位置示意图
1.2 粘弹性边界的设置与模型单元的选取
在地下结构的动力有限元分析中,为处理结构反射波在模型边界处的二次反射问题,需设置粘弹性边界来模拟边界处的应力和位移连续条件[14]。本文使用COMBIN14单元,即弹簧-阻尼器单元在模型的左、右、下3个模型边界处形成相应的人工粘弹性边界条件。根据文献[15],取人工边界法向修正系数αT=1.0、切向修正系数αN=0.5,计算得到模型人工边界的法向弹簧刚度KBT=62 758.8 kN/m3、切向弹簧刚度KBN=125 517.6 kN/m3、法向阻尼系数CBT=53 460.0 kg/(m2·s)、切向阻尼系数CBN=93 871.8 kg/(m2·s)。
地层、管道、支墩均采用实体类PLANE183单元,管廊结构则采用BEAM3梁单元。
1.3 地震波的选择
本文所研究的管廊处于二类场地中,输入地震波选用适用于该类场地的El-Centro波。El-Centro波采样频率为50 Hz,持续时间54 s,包含3个方向的地面运动数据,本文选取南北(N-S)方向数据,其峰值加速度为334.482 cm/s2,并截取代表了能量释放特性的前20 s数据作为输入地震波。在图3所示模型中,地震波采用水平自左向右入射。
2 管道对综合管廊地震响应的影响分析
通过有限元软件模拟计算,得到地震作用引起的4种工况下综合管廊结构动力响应。本文针对动力响应中对结构抗震安全影响最大的应力和位移展开分析。
在水平地震作用下,地下结构各构件连接点处的应力显著大于构件跨中部位的应力[8],为此,应力分析主要针对墙板连接点附近的观测点。同时,因混凝土结构的抗拉强度远小于其抗压强度,结构第三主应力的工程意义不大,所以在主应力分析时仅考虑第一主应力的变化情况。在位移分析观测点选择时,考虑到构件连接点处各观测点间距很小,位移响应差别不大,因此构件连接点处仅取典型观测点进行分析。
2.1 第一主应力分析
通过对各工况有限元模型的数值计算,得到的管廊观测点第一主应力峰值以及工况二、三、四的主应力峰值相对工况一的变化率如表2所示。
由表1可知,工况二、工况三、工况四的第一主应力峰值与工况一的差异较大,说明大质量管道的存在对管廊结构动应力分布影响十分显著,综合管廊抗震设计中考虑大质量管道的影响是必要的。
工况一下未考虑综合管廊内管道影响,此时结构的第一主应力最大值为0.481 MPa,出现在W4-1观测点,即下层结构中隔墙顶部位置,且中隔墙上的应力大于其余构件上的应力,同时,结构下层A3仓构件第一主应力明显高于A1仓和A2仓。该现象表明水平地震波入射导致管廊结构形成显著的压拉应变,且A1仓与A2仓的应变沿地震波传播方向传递至A3仓,导致A3仓形成应变的叠加。
工况二下管道位于A1仓,应力增幅最大的点为W4-3点,即中隔墙与底板连接处,增幅高达41.6%,同时,A1仓底板、A3仓各构件应力均存在增大的现象。上述现象表明地震作用引起的管道惯性力主要由中板传递至下层结构中隔墙后向A3仓方向扩散,中隔墙应力重分布现象最为显著。
工况三下管道位于A2仓,应力增幅最大的点仍是W4-3点,但较工况二有所减小,增幅为36.9%,P3-1、W2-3点处应力增幅均超过10%,A2仓和A3仓各构件应力增幅明显大于A1仓。表明该工况下管道惯性力对上层结构影响不大,惯性力主要在下层结构传递并导致各构件应力分布的变化。
工况四下管道位于A3仓,W4-3点处应力增幅仍最大,增幅与工况三相当,但其余观测点处未出现增幅超过10%的现象。表明工况四下管道惯性力仍在下层传递,且对A2仓影响不大。

表2 管廊观测点第一主应力峰值及对比
综上,在L形三仓管廊内部管线布置时,大质量管道的存在导致中隔墙应力增幅显著,从第一主应力的角度来看,当管道布设在上层分仓时管道惯性力传递路径复杂,对结构抗震最为不利,管道布置在管廊下层且远离震源方向的分仓最为合理。
2.2 剪应力分析
计算得到的管廊观测点剪应力峰值及工况二、三、四的剪应力峰值相对工况一的变化率如表3所示。
由表3可知,工况一情况下管廊结构剪应力最大值出现在观测点W4-1和W4-3位置,剪应力峰值接近1 MPa,即地震作用引起结构最大剪应力位于中隔墙上,其余各构件上观测点处剪应力较小,且差别不大。这一结果与日本阪神地震中地铁车站中柱发生剪切破坏的现象具有一致性,说明上层分仓形成的惯性运动主要沿中隔墙传递。
管道位于A1仓时,剪应力峰值增幅最大的点位于P5-1,即中隔墙与底板连接处,剪应力增幅为23.0%,其余各观测点处增幅均不超过10%,说明中隔墙传递的剪应力较大;管道位于A2仓时,剪应力在P3-1、P5-1和W2-3三点处增幅分别达到15.7%、18.9%和13.9%,即管道所在仓体边墙底端附近剪应力变化突出,但其峰值仍小于中隔墙剪应力,其他点处则几乎未出现增长现象;管道位于A3仓时,仅W5-3点处剪应力增幅最大为10.2%,位于管道所在仓体右边墙底端,增幅较大的P5-1和P5-3两点则位于管道所在的A3仓底板上,且增幅仅有5%左右,中隔墙上剪应力几乎不受影响,表明剪应力沿地震波入射方向向右传递,管道的存在对结构地震响应影响较小。
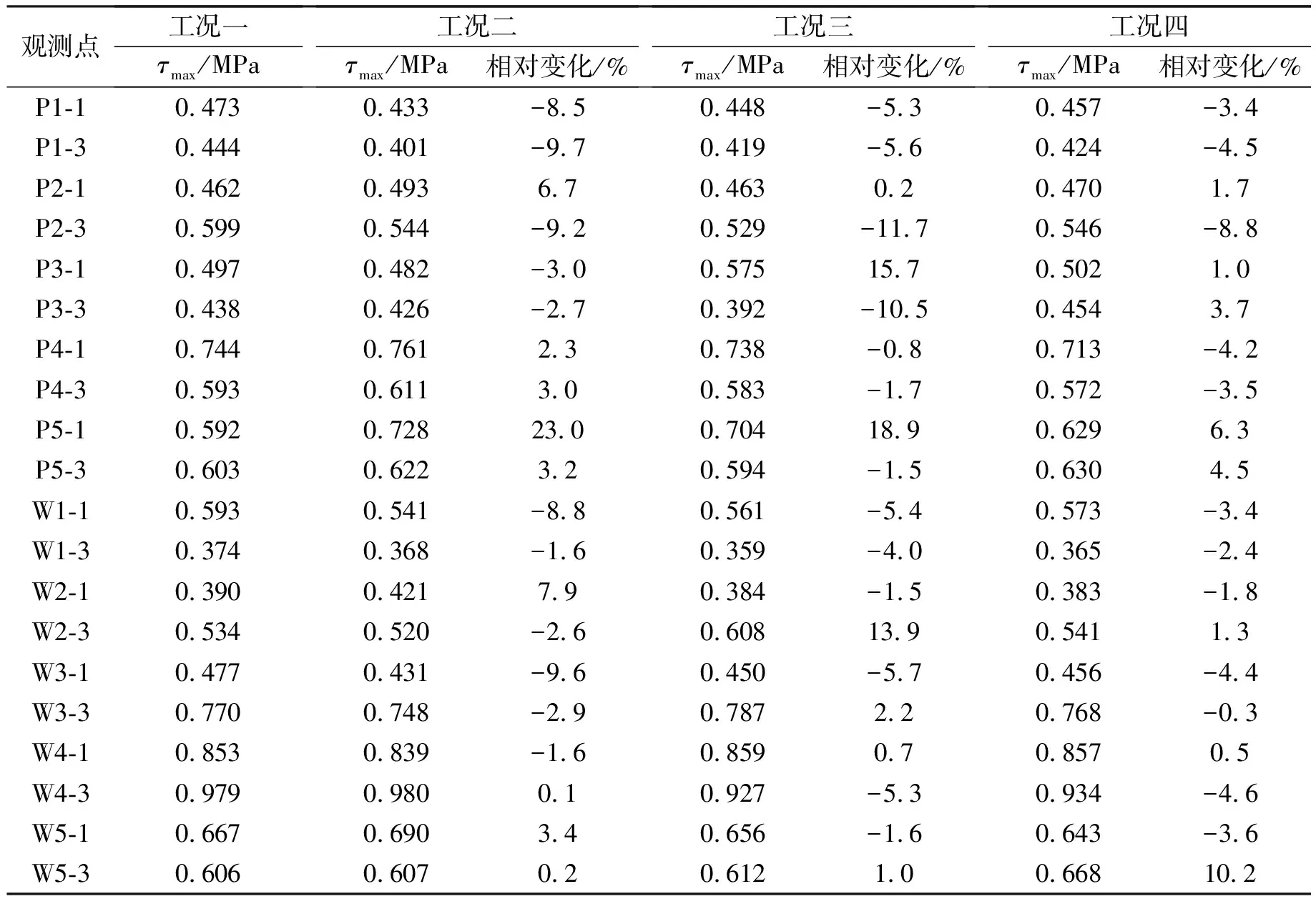
表3 管廊观测点剪应力峰值及对比
可见,与第一主应力情况类似,当管廊内设置大质量管道时管廊结构的剪应力发生重分布,管道布置在地震波入射一侧分仓内,尤其是在上层分仓内时,中隔墙的剪应力受管道影响很大,当管道布置在远离震源的分仓内时,剪应力传递路径相对简单,结构地震响应受管道影响最小。
2.3 位移分析
计算得到的各观测点处水平位移峰值及工况二、三、四的位移峰值相对工况一的变化率如表4所示。
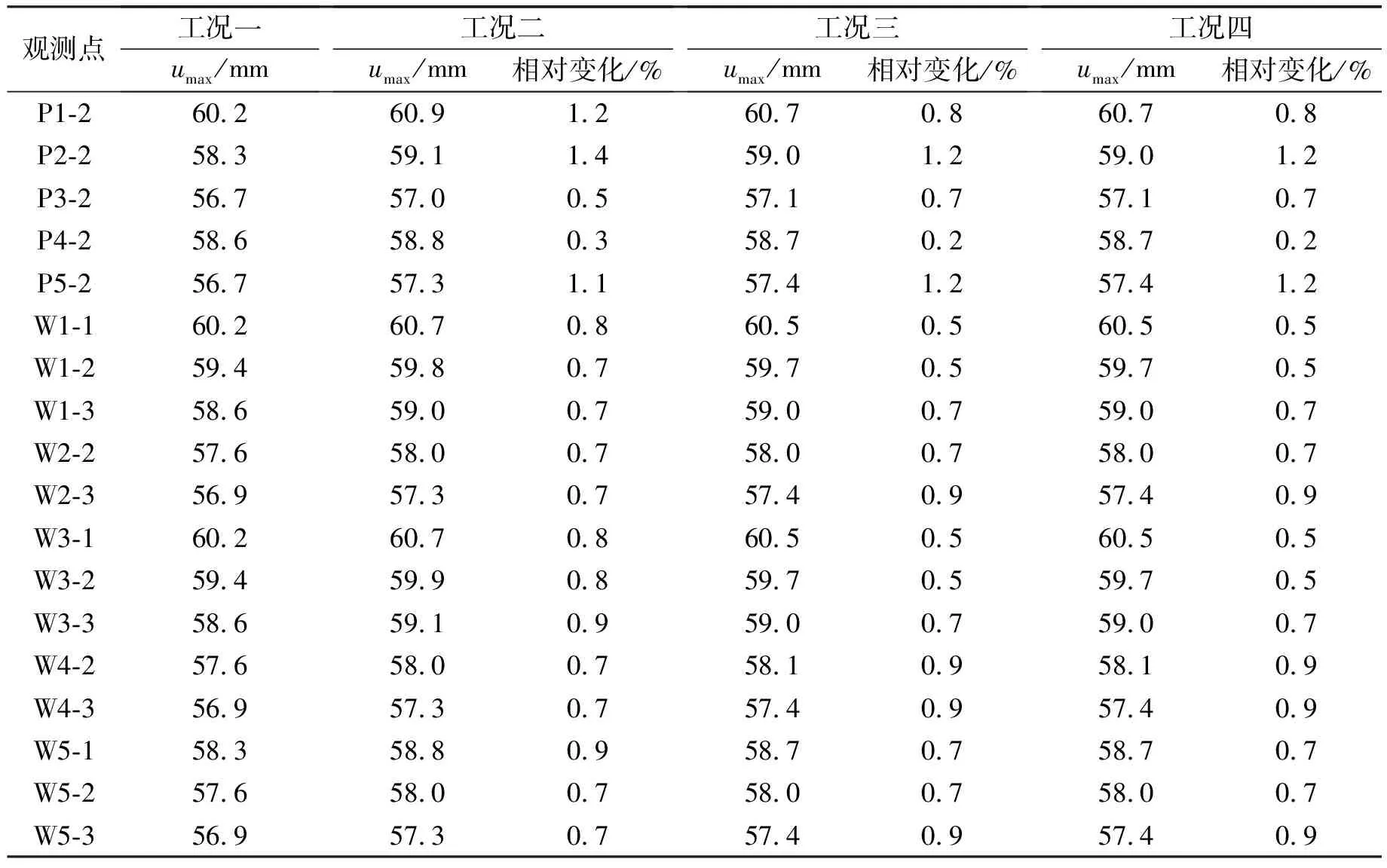
表4 管廊观测点水平位移峰值及对比
根据表4,水平地震波作用下综合管廊各观测点处的水平位移峰值集中于56~61 mm之间,表明管廊结构整体随场地发生共同运动,但由于结构与场地的动力学参数存在差异,管廊各构件在地震过程中仍发生了幅度不大的扭曲变形。4种工况下位移最大值均出现在顶板跨中,位移最小值则出现在A2仓底板跨中,工况一下水平位移最大相差3.5 mm,当设置大质量管道后,工况二下的最大差值增大至3.9 mm,工况三和工况四下则为3.6 mm,可见,大质量管道的存在造成结构水平位移差值的增大。但是,考虑大质量管道时的水平位移峰值与无管道工况下的差异很小,相对增幅仅1%左右,可认为管道的存在对结构位移几乎不产生影响。
3 结 论
本文以某在建综合管廊工程为背景,运用有限单元法计算得到了含大质量管道的综合管廊结构的地震响应,并分析了水平地震作用下管道对结构第一主应力、剪应力、水平位移等参数的影响规律。得到的关键结论包括:
(1)在水平地震作用下,L形三仓管廊中隔墙的动应力最大;
(2)大质量管道可以导致管廊结构动应力的重分布,当管道位于上层分仓时,管道惯性力传递路径复杂,结构动应力增幅最大,对结构抗震最不利,当管道位于下层且远离震源方向的分仓时结构动力响应最小;
(3)水平地震波作用下综合管廊结构整体随场地发生共同运动,各构件产生一定的扭曲变形,内置大质量管道对管廊结构的水平位移几乎不产生影响。
