骰子的组合数探究
2020-03-16四川省宜宾市南溪区第一中学张玄逸
数学大世界 2020年3期
四川省宜宾市南溪区第一中学 张玄逸
如果能够仅仅通过交换而不改变数值得到的组合只算作一个组合,比如——
那么这一组骰子可以掷出多少不同的组合?

可惜的是作者并没有给出证明过程。
骰子与组合无法直接建立特定倍数关系,因为骰子们点数的种类和数量都是变量。
本文试从公式出发倒推证明过程,最终回归组合。
一、排序
首先必须把每个数列中的数字重排。有序数组更易发现规律。将其记为ai。
二、构造数组
构造bi,b1表示有几个1,b2表示有几个2,以此类推。上述组合可以改写为:0 2 1 0 2 1,
另外有很明显的几点:a1≥1 ;a6≤6 ;ai-1≤ai。
看似平常的三点可以启发我们构造另一个数组:
令ci=ai-ai-1,即ci为ai的差分数组。
经验证,两个数组均可以推导得到公式,因此下文就以更难一点的差分数组来证明。
三、规定
差分数组的含义为当前数字比前一个多了多少,那么c0该等于几?根据后面的ci范围为[0,5],类比得到c0=1,c1∈[0,5],否则下一步操作无法等价进行。
四、隔板法
现在已经类似于隔板法了,因为最后一个数最多比c0多5,所以有5 个小球。因为最后一个数不一定为6,因此隔板仍需6 块,而相邻两隔板间的距离即为ci。但会导致此种情况。以上文2 2 3 5 5 6 为例。
隔板法不允许两隔板置于相同空隙中。

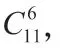
抽象数组仍需使用隔板法,只是两隔板间距含义为使用该数字的个数,且使用数字总数确定,因此需要(6+5)个小球和5 块隔板。

