肯斯瓦特水库极限防洪的风险分析

2020-03-14张鑫厚陈伏龙

石河子大学学报（自然科学版） 2020年1期

张鑫厚，陈伏龙

(石河子大学水利建筑工程学院，新疆石河子 832003)

随着全球气候变暖和人类活动对流域下垫面干预的加剧，水文序列失去了一致性，洪水样本的独立同分布假定已遭到极大挑战[1]，采用传统频率分析方法得到的工程设计结果的可靠性倍受质疑[2-3]，因此，采用非一致性洪水频率计算方法分析水库防洪安全显得十分必要。水库下游用水需求的增加对水库汛期的防洪调度提出了更高的要求，即不仅能够在汛期保证水库的安全，还要充分利用洪水资源[4]，因此对水库进行防洪风险分析具有实际意义。目前，国内许多专家学者对此作了研究，姜树海[5]采用事故树分析方法分析了漫坝失事的形成原因，得出了相应的风险率，并论证了合理选择大坝防洪设计标准的原则和方法；李响等[6]将预泄能力约束法与蒙特卡洛随机模拟相结合，同时考虑洪水预报误差及洪水过程线形状不确定性等因素，在控制汛期防洪风险的条件下推求三峡水库汛限水位动态控制域；吴成国等[7]以潘家口水库为例，将三角模糊数理论运用于水库防洪调度风险分析，结果表明该方法能够全面地估计调度过程中的各种风险因子；李大鸣等[8]采用Copula函数构建洪峰洪量两变量模型反映水文不确定性，并应用Monte Calro方法计算了桃林口水库的防洪风险率；黄凯[9]采用水文变异诊断系统对比分析了过去、现在条件下的极限防洪风险率，从而进一步提高了环境影响下的预报精度；李平[10]等将贝叶斯网络引入梯级水库防洪风险计算中，结果表明贝叶斯网络方法能直观、简便地分析出多种风险因素共同作用下的水库群连溃风险。

干旱环境、气候变化和人类活动的共同影响，以冰雪融水为基础的水资源系统非常脆弱，使得区域水循环系统的稳定性和水资源的可再生性降低，极端水文事件发生的频度和强度增大[11]。玛纳斯河流域以融雪洪水与暴雨洪水混合为主，其洪水总量较高，洪水过程线多宽缓等特点[12]，对该流域年最大洪量序列的研究符合洪水特点，对确保水利工程防洪度汛安全和制定防洪调度方案具有重要意义，对于肯斯瓦特水库防洪风险的研究结果可为玛纳斯河水库防洪及汛期洪水资源利用提供指导依据。

1 研究区概况

本文以玛纳斯河上游肯斯瓦特控制流域段为研究区域，如图1所示。肯斯瓦特水文站是玛纳斯河干、支流汇合后的出山口控制站，海拔约910 m，控制流域面积为4 637 km2，多年平均年径流量12.21亿m3。肯斯瓦特水库具有防洪、灌溉、发电等多种功能其正常蓄水位990 m，最大坝高129.4 m，总库容1.88亿m3，控制灌溉面积21.10万hm2，属于大(2)型工程；其设计洪水标准为500年一遇，相应的洪峰流量为2 382 m3/s，校核洪水标准为5 000年一遇，相应的洪峰流量为3 601 m3/s，下游防洪保护标准为50年一遇，相应的洪峰流量为1 249 m3/s。

图1 肯斯瓦特控制流域

2 洪量序列变异点检验

2.1 基于Pettitt法变异点检验

采用Pettitt非参数检验法[13]对玛纳斯河肯斯瓦特控制流域融雪洪水年最大洪量序列进行变异点检验，结果(图2)显示：年最大一日洪量序列可能在1993和1995年发生变异，年最大三日洪量序列可能在1993、1994、1995和1996年生变异，年最大七日和十五日洪量序列可能在1994、1995和1996年发生变异。取统计量P值最大的年份为最可能发生的变异年份，因此，年最大一日洪量序列变异点为1993年，年最大三日、七日和十五日洪量序列变异点为1995年。

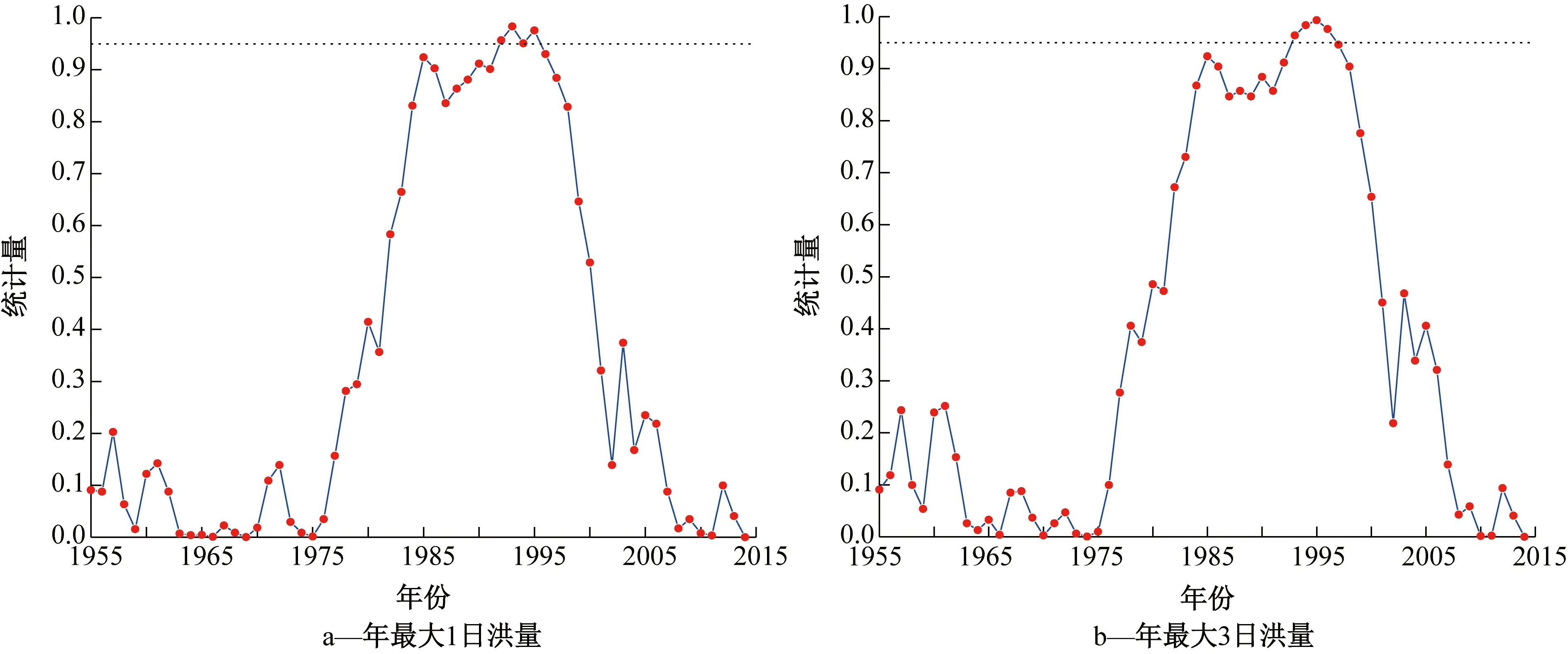
图2 Pettitt法变异点检验结果

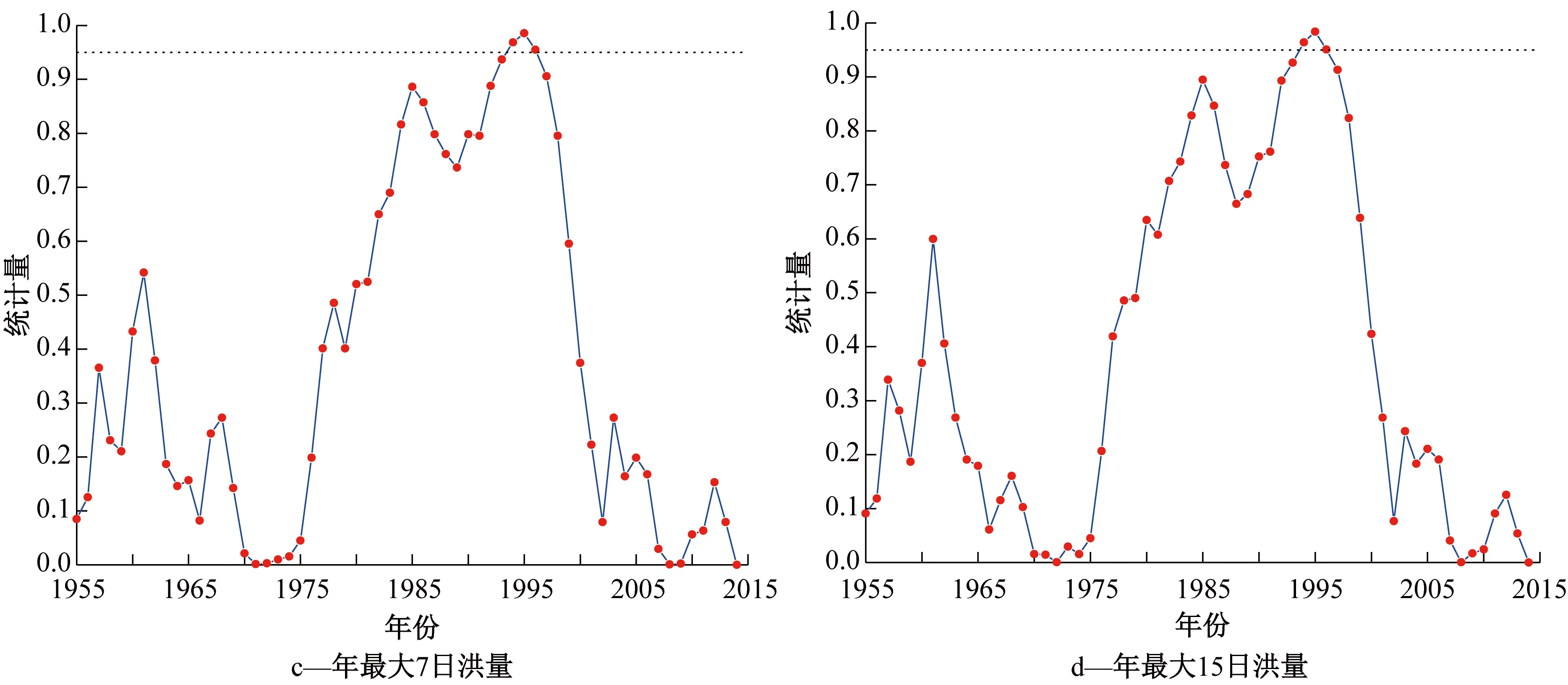
图2(续)

2.2 基于可变模糊法变异点检验

可变模糊集检验法基于陈守煜[14]提出的质变与量变定理，由LI Jianzhu等[15]提出并应用于变异点检验。该方法基于序列的均值进行计算，对于序列的异常值不敏感。

对玛纳斯河肯斯瓦特水库控制流域融雪洪水年最大洪量序列分别选用基于三角模糊数的变异点检验法进行变异点检验，其结果如图3所示。

图3 可变模糊集法变异点检验结果

从图3可以看出：年最大洪量序列均发生质变，即发生跳跃性变异，其中，年最大一日洪量序列发生变异年份为1993年，年最大三日、七日和十五日洪量序列发生变异年份为1995年，综合两种方法认为该结果能真实反映出年最大洪量序列的变异情况。

3 洪量序列一致性修正

3.1 序列分解计算

根据谢平等[16]提出的“分解-合成”理论及非一致性水文序列频率计算方法，洪水序列由两种或两种以上成分线性叠加而成。根据Pettitt检验与可变模糊集变异点检验的结果，肯斯瓦特控制流域1957—2014年年最大一日洪量序列在变异点1993年可分为2个子序列，年最大三日、七日、十五日洪量序列在变异点1995年可分为2个子序列，其结果见表1。

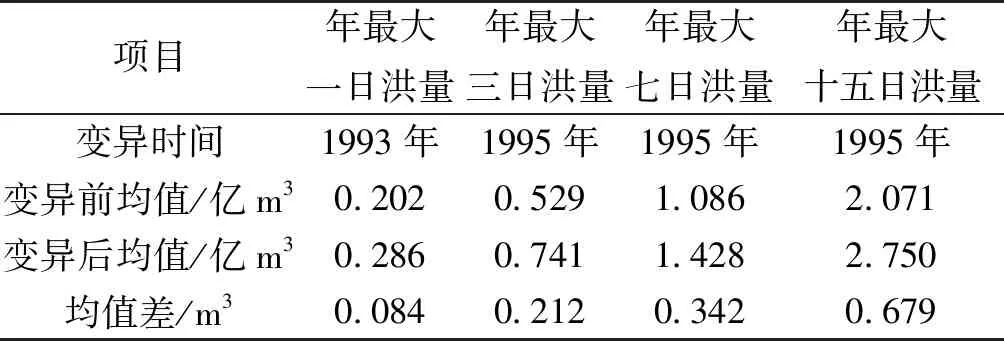
表1 年最大洪量序列分解计算成果

根据水文时间序列的线性叠加原理，可求得年最大洪量序列的确定性成分Yt，按公式(6)可求出肯斯瓦特控制流域1957—2014年年最大洪量序列剔除跳跃成分后的随机序列，如图4所示。此序列为过去条件下年最大洪量序列，受自然条件变化影响较小，可以满足洪水序列的一致性要求。

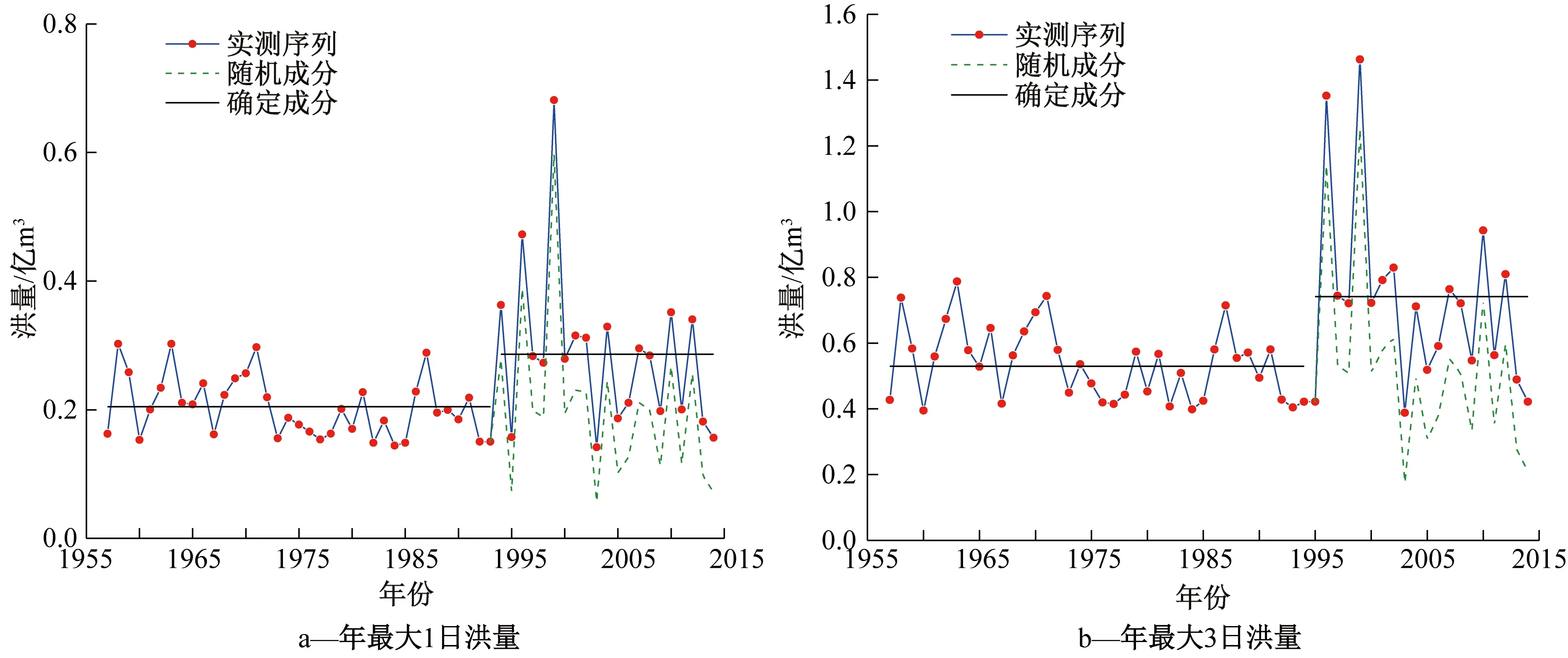
图4 年最大洪量序列分解结果

3.2 序列合成计算

假设过去条件下年最大洪量序列服从P-Ⅲ型分布，可采用优化适线法[17]得到过去条件下年最大洪量序列。采用蒙特卡洛法随机模拟生成500个随机性成分Sp，并结合t时刻(2014年)求出确定性成分Yt，利用以下合成公式

Xt,p=Yt+Sp

(1)

获得现状条件下(2014年)年最大洪量序列的样本，通过优化适线法对其进行P-Ⅲ型分布拟合，得到现状条件下年最大洪量序列统计参数，结果见表2，相应频率的设计值见表3。

由表3可以看出：现状条件下的年最大洪量序列设计值比相应频率下2008规划的设计值均有所增加，变化幅度为1%～20%，其中年最大七日洪量与年最大十五日洪量变化量均超过了10%。根据邹全等[18]的研究可知，主要是因为流域气温显著上升和气候的变化导致水文极端事件发生的频率增加。因此，为保证肯斯瓦特水库在汛期安全运行的前提下，对洪水资源进行充分利用，有必要在非一致性年最大洪量序列条件下，对水库极限防洪风险进行分析。

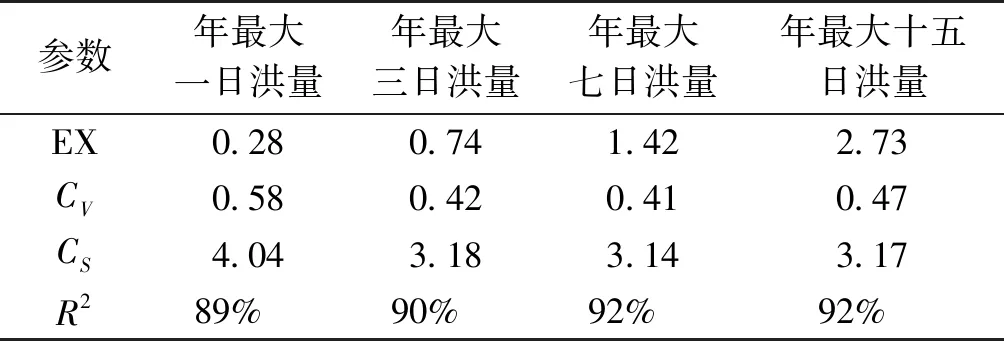
表2 现状条件下年最大洪量序列统计参数

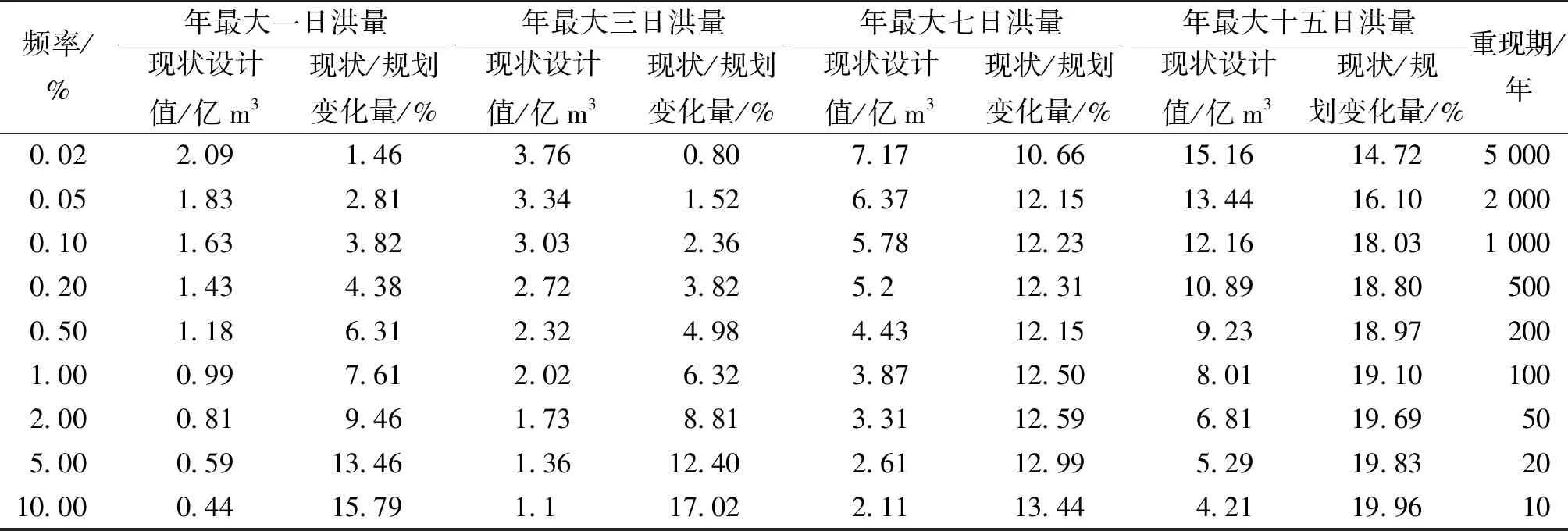
表3 现状条件下年最大洪量设计值

4 极限防洪风险分析

近年来，许多国内外学者针对于水文不确定性所带来的风险做了大量的研究，提出了一些计算防洪风险率的方法，主要有频率分析法、随机微分方程法、随机模拟法。本文选择频率分析法和基于三角模糊数风险分析法对肯斯瓦特水库现状条件下不同频率的融雪洪水设计值分别进行水库极限防洪风险率计算。

4.1 基于频率分析法风险分析

传统的频率分析法中假设水库年调洪最高水位与年最大洪水出现的频率相同，以年调洪最高水位等于不破坏水利工程指标水位的洪水频率作为水库极限风险率。具体的计算步骤为：首先指定一个水库极限防洪风险控制指标Zd，计算出不同设计频率Pi(i=1,2,…,l)下入库设计洪水过程，然后根据起调水位Z0并结合水库防洪调度规则进行调洪演算，通过不断的试算，计算出l个最高库水位Zmi(i=1,2,…,l)，最后建立Zmi～Pi经验频率曲线，并依据此频率曲线可由Zd值反查出水库极限防洪风险率Pf(Zm≥Zd)。

4.1.1 调洪规则

通过河道过流能力分析，结合防洪工程的总体布局，从防洪要求出发，设定汛期限制水位为984 m、下游泄量为500 m3/s，以此作为控制条件进行调洪演算，其中调洪规则为：

当入库洪水小于50年一遇的标准时，水库水位低于防洪高水位992.66 m，控制水库的洪水下泄，最大下泄洪水为500 m3/s。

当入库洪水大于50年一遇标准时，水库运行按照水库水位分时段控制：当入库洪水小于下游安全泄量500 m3/s时，来多少泄多少，维持水库汛限水位984 m不变。当水库水位高于984 m低于防洪高水位992.66 m，且入库洪水大于下游安全泄量500 m3/s时，下泄量按下游安全泄量500 m3/s下泄。当水库水位超过防洪高水位992.66 m时，若入库洪水流量小于泄洪建筑物下泄能力，按入库洪水流量下泄，维持防洪高水位；若入库洪水流量超过泄洪建筑物下泄能力时，按泄洪建筑物的泄流能力自由下泄。退水段水位逐渐下降至汛限水位后，若入库洪水流量小于泄洪建筑物泄流能力，则维持汛限水位不变；若入库洪水流量大于泄洪建筑物泄流能力，则按泄洪建筑物的泄流能力自由下泄。

4.1.2 防洪风险率计算

以1996年典型融雪洪水过程为基础，通过同频率放大法计算现状条件下不同频率设计融雪洪水过程，并作为入库融雪洪水，根据水库水位—库容—泄量关系曲线，结合肯斯瓦特水库调度运行规则，经调洪演算计算出设计洪水条件下的调洪结果，见表4。

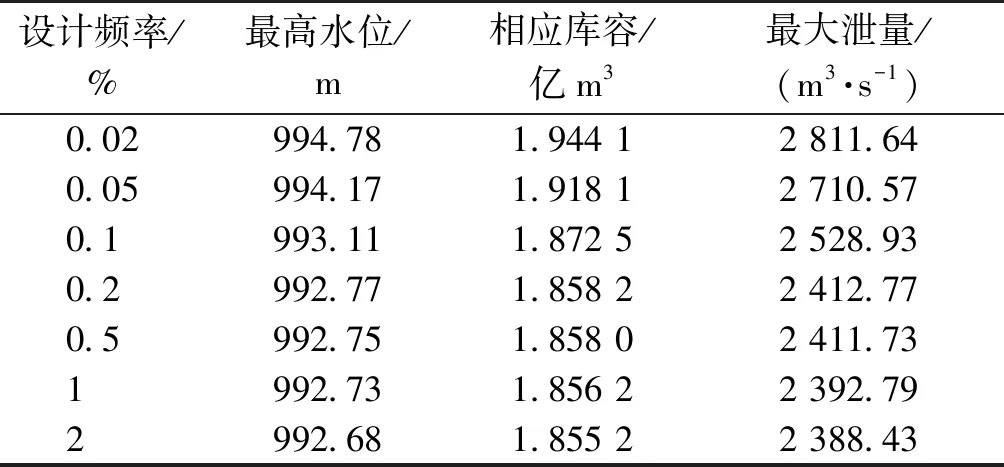
表4 现状条件下水库调洪成果表

按表4中不同设计频率所对应的汛期最高库水位建立现状条件下最高库水位与设计频率之间的相关关系，即Zmi—Pi经验频率曲线(图5)，并按此频率曲线由Zd值反查出水库的极限防洪风险率Pf(Zm≥Zd)。

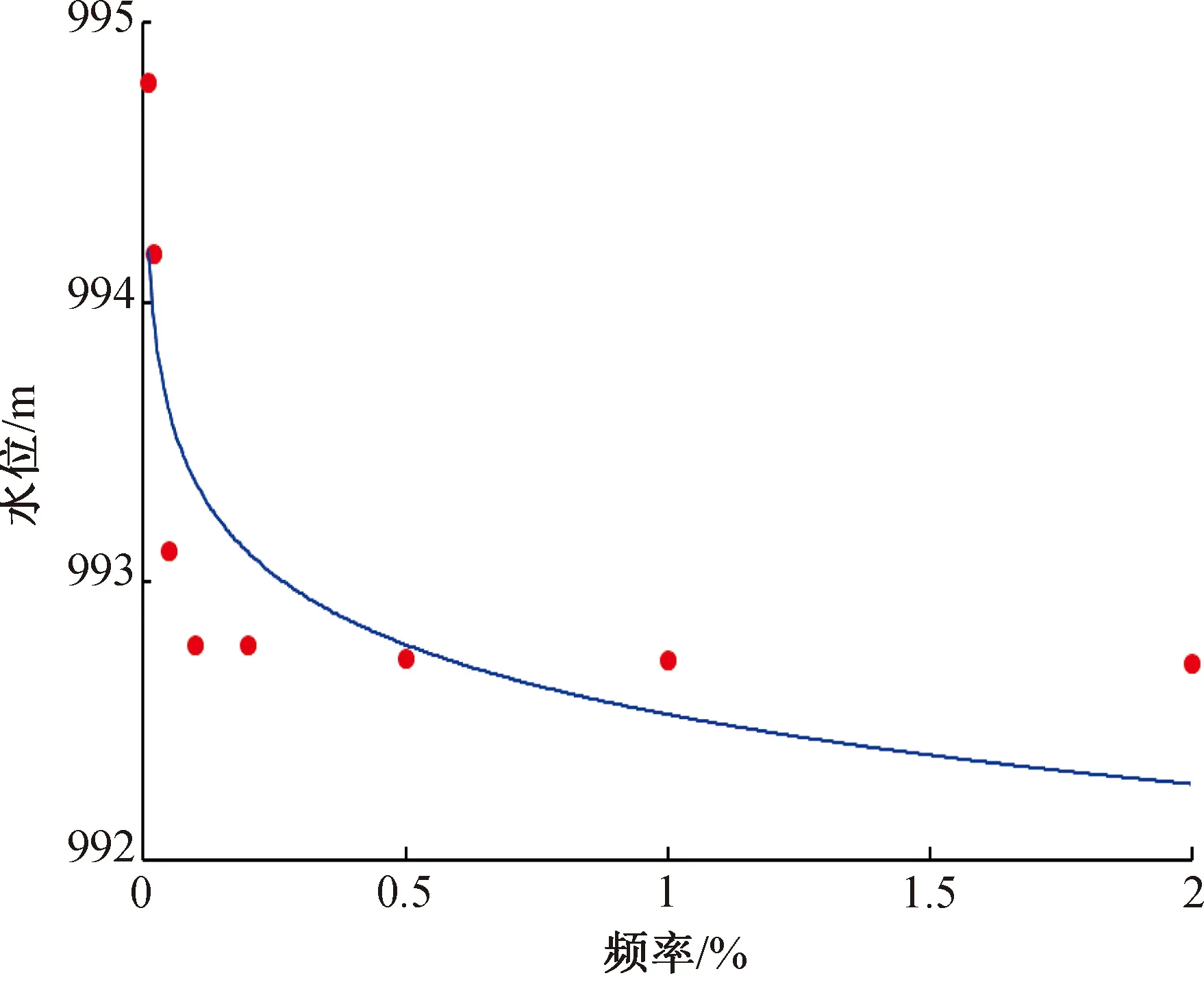
图5 Zmi—Pi经验频率曲线

从表4可知，现状条件下肯斯瓦特水库0.02%设计频率所对应的最高库水位Zm=994.78 m。

以水库校核洪水位Zd=993.66 m，由图5查得其水库极限防洪风险率Pf(Zm≥Zd)=0.123 7%>0.02%。这表明肯斯瓦特水库控制流域气温、降雨量以及融雪洪水径流量的变化会导致现状条件下水库极限防洪风险增大。

4.2 基于三角模糊数法风险分析

4.2.1 三角模糊数

三角模糊数[7]定义了隶属度函数的区间数，这一较确定性实数能更好地描述和表征复杂系统的波动性和不确定性特征[19]。

本文设a1、a2、a3分别为一模糊变量的最小可能值(下限)、中值和最大可能值(上限)，则可建立一个三角模糊数，即

A=(a1,a2,a3)，a1≤a2≤a3。

三角模糊数不同置信度水平所对应的区间数长度不同。设α为置信度水平，且α∈[0,1]，则可将三角模糊数A转化为与一定置信度水平α相对应的区间数，记

[(a2-a1)α+a1,-(a3-a2)α+a3]，

称Aα为三角模糊数A的α-截集，它实际上是置信度水平不低于α的数据集合。

4.2.2 抽样方法

根据历史实测洪水特征值之间相互独立的特性，采用自回归模型对洪水过程进行随机模拟[20]。本文选用一阶自回归模型AR(1)，其基本形式为

Xt=u+φ1(Xt-1-u)+ηt，

(2)

式(2)中：Xt为时间序列，φ1为一阶自回归系数，ηt为独立随机序列，u为序列均值。

对于洪水序列，独立随机序列ηt一般采用P-Ⅲ型分布，故式(2)可变为

(3)

式(3)中，r1由尤尔-沃尔克方程求得，σ为序列标准差，φt为标准化的P-Ⅲ型分布。

本文采用此一阶自回归模型进行洪水特征量的随机模拟，在肯斯瓦特水库风险分析中，以1996年一场大洪水作为典型洪水，随机模拟10万次洪水组成入库洪水序列。

4.2.3 极限防洪模糊风险率计算

以5 000年一遇洪水调洪所得最高水位994.78 m作为模糊变量的上限值，防洪高水位992.66 m作为模糊变量的下限值，校核洪水位993.35 m作为模糊变量的中值，同时对置信度水平α在[0,1]中取不同值，可得与不同置信度水平α相对应的水库校核水位模糊变化区间结果，见表5。

对随机生成的10万条入库洪水过程线设定一置信度水平α值，可得一组水库校核水位的模糊变化区间，再通过统计计算得到一组水库极限防洪的模糊风险率区间值，结果见表6。

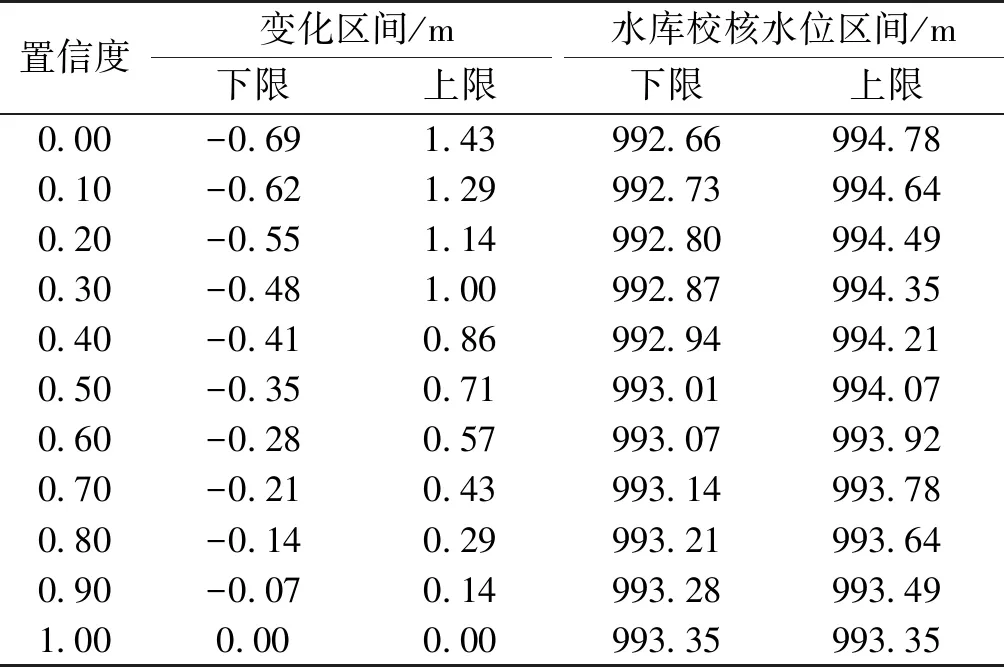
表5 不同置信度水平下水库校核水位的变化区间α

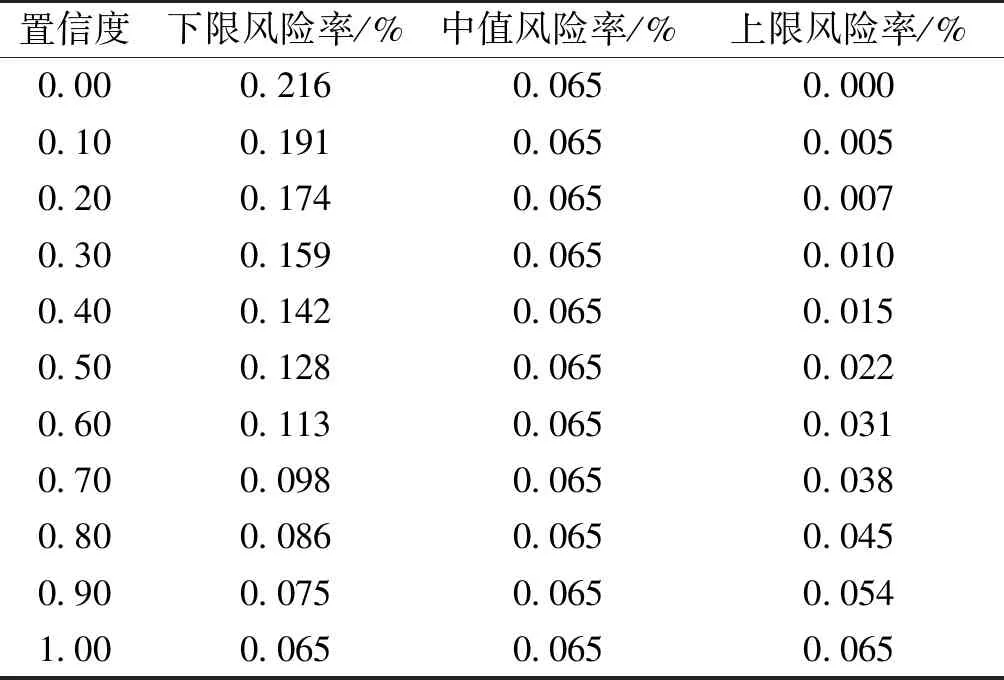
表6 不同置信度水平下水库极限防洪的模糊风险率区间α

从表5和表6可知：

(1)当截集水平α=0.0时，水库风险率区间范围最大；随着截集水平α的逐渐增大，水库极限防洪风险指标模糊区间的范围逐渐减小。这表明数据的模糊性逐渐减弱，提高了风险指标模糊区间内数据的可信度水平。

(2)当截集水平α=1.0时，其所对应的区间表示风险指标和风险率的相对最概然区间。这反映出水库洪水调度过程中从风险出现到风险加剧进而致灾的一个缓变过程，而采用传统的方法进行水库极限防洪风险分析，风险指标的估计值为一个点值，因此，风险模糊区间比传统的风险率计算确定值更符合实际，可以为决策者提供更多的参考信息。

(3)两种方法所得到的极限防洪风险率，均比0.02%要大。其主要原因在于流域气温呈显著上升趋势，温度升高引起以冰雪融水为基础的融雪洪水径流的季节性变化，改变了流域降水、融雪洪水径流的时空分布和原有产汇流过程，使融雪洪水径流过程产生变化，造成融雪洪水特征序列的变异，使得肯斯瓦特水库控制流域年最大洪量序列呈现增加的趋势。