均匀线阵中基于降秩Capon的近场源定位

陈未央，徐 乐，张小飞

（南京航空航天大学电子信息工程学院，南京，211106）

引 言

空间信源定位是阵列信号处理领域中的一项关键技术，它在医学成像、雷达、无线通信、声呐等方面都有着广泛的应用[1-2]。针对这一问题，国内外学者已经提出了多种经典算法，其中，包括最大似然(Maximum likelihood,ML)算法[3-7]、借助旋转不变性估计信号参数(Estimation of signal parameters via rotational invariance techniques,ESPRIT)算法[8-10]、基于子空间理论的多重信号分类(Multiple signal classification,MUSIC)算法[11-13]等。根据信源距离接收阵列的远近，空间信源定位又可分为近场信源定位和远场信源定位。对于近场信源而言，信号入射至各个阵元时产生的相位差是关于阵元位置的非线性函数，因此远场信源波达方向(Direction of arrival,DOA)的估计方法大多不能直接应用于近场信源定位。对于近场来说，空间信源的定位问题不仅与信源的波达方向有关，还与信源与阵列之间的距离有关。因此，近场信源定位的数据模型中，既包括信源的角度信息，也包括距离信息，这样能够更加准确地描述信源在空间中相对于阵列的位置。

针对近场信源的定位问题，国内外学者做了大量研究工作，提出了多种应用于近场的信源定位方法，根据原理的不同，可大致分为非谱峰搜索和谱峰搜索两类。非谱峰搜索类的算法一般借助二阶或高阶统计量，通过计算闭式解得到信源的参数估计。近年来学者们提出了多种基于二阶统计量的算法[14-15]。由于高阶统计量具有保持信号相位并去除高斯噪声干扰的良好特性，一些基于高阶统计量的算法也被陆续提出[16-17]。由于不需要进行谱峰搜索，该类算法的计算复杂度普遍较低，但信号参数的估计精度也明显降低。同时，该类算法需要多次矩阵分解操作，且需要对所获得的参数估计进行额外配对[18-19]。

谱峰搜索类算法的共同特点是估计精度高，但计算量巨大。Swindlehurst等[20]首先提出了基于最大似然的近场源参数估计方法，该方法具有优异的统计特性，但计算复杂度非常高。Huang等[21]证明了信源位于近场时，子空间理论中信号子空间和噪声子空间的正交特性依然是成立的，并由此提出了基于近场信源的经典二维MUSIC算法，该方法估计精度高，但由于需要二维全局空域空间谱搜索，所以计算量同样巨大。近年来，许多其他近场信源定位算法被提出，如Root-MUISC算法[22]、路径跟踪法[23]、加权线性预测法[24]、改进型路径跟踪算法[25]等，这些算法均对已有算法进行了改进与优化，在一定程度上降低了计算复杂度。

从上述两类算法的介绍与分析中可知，如何有效地降低计算复杂度，避免谱峰搜索和进行参数配对，同时最大限度地提升参数估计精度，是近场信源定位技术研究的关键点。基于此，本文将矩阵降秩思想与Capon算法结合，对经典的近场源估计方法进行简化，提出了一种均匀线阵中基于降秩(Rank reduce,RARE)思想的近场源参数估计方法。本文的主要贡献如下：(1)提出了基于降秩思想的角度和距离参数联合估计方法；(2)相较于经典二维Capon(Two-dimensional Capon,2D-Capon)算法，本文算法避免了二维谱峰搜索，大大减小了计算复杂度；(3)本文算法的参数估计性能接近经典2D-Capon算法，具有较高的参数估计精度；(4)本文算法无需信源数估计。

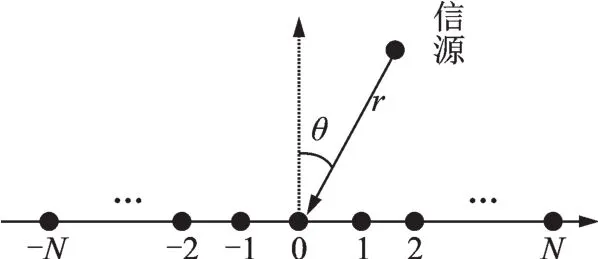
图1 近场信源定位均匀线阵模型Fig.1 Structure of uniform linear array for near-field sources localization

1 数据模型

如图1所示，方位角与距离分别为(θk,rk)的K个近场信源发射信号，入射到由M=2N+1个沿x轴均匀排列的阵元组成的均匀线阵上，选取中心阵元为阵列的相位参考点。对于近场信源而言，信源的距离满足rk∈[0.62(D3/λ)1/22D2/λ]，其中λ为信源波长，D为阵列孔径。此时信源位于阵列的菲涅尔区域，信号到达阵列时呈球面形式[20]，不能再近似为平面波。假设K个接收信号互不相关且具有相同的中心频率ω0，阵元间距不大于四分之一波长[24]。

则第m个阵元上的接收信号可以表示为[26]

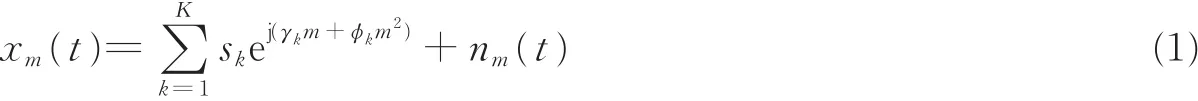
式中：γk=-2πd sin θk/λk；φk= πd2cos2θk/λkrk；sk(t)表示第 k个信源发出的信号被第 m 个阵元接收并解调后的基带信号；nm(t)表示阵元上的加性噪声；θk∈[-π/2,π/2]为第k个信号入射方向的反方向与y轴之间的夹角；λk为第k个信号的波长；rk为信源到参考阵元之间的距离。将式(1)写成矩阵的形式为

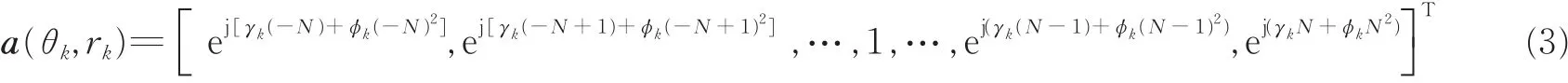
利用J个快拍的接收信号，可以计算信号协方差矩阵为

为不失一般性，本文做如下假设：

(1)信源为相互统计独立的窄带随机过程，零均值，具有非零功率，信源的波长归一化为1；

(2)阵元接收噪声为零均值、白或色高斯噪声，并与信源统计独立；

(3)对于不同的信源，即 i≠ j，相位参数各不相同，即满足 γi≠ γj，φi≠ φj；

(4)阵元为全向阵元且响应特性完全相同，无通道不一致、互耦等因素的影响，空间增益为1，阵元间距满足 d ≤ min(λ1/4,…,λK/4)；

(5)阵元个数与信源个数满足K≤N。

2 降秩Capon算法

在经典的近场2D-Capon算法中，信源参数(θ,r)可通过式(5)在空域中进行全局谱峰搜索得到

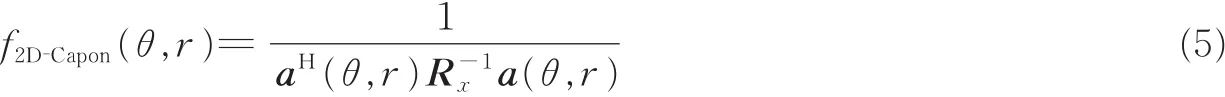
式中 a(θ,r)为

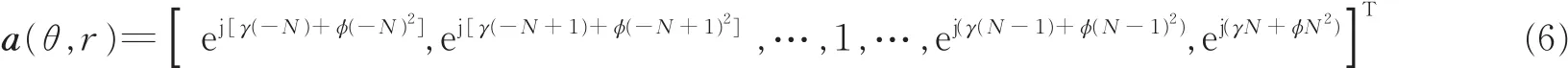
经典2D-Capon算法需要全局二维谱峰搜索，复杂度很高。为了降低算法复杂度，本文借鉴降秩思想，提出降秩Capon算法来实现二维参数估计，该算法有效避免了高复杂度的二维谱峰搜索过程。

由于阵列结构的对称性，导向矢量可以分解成如下形式[27]

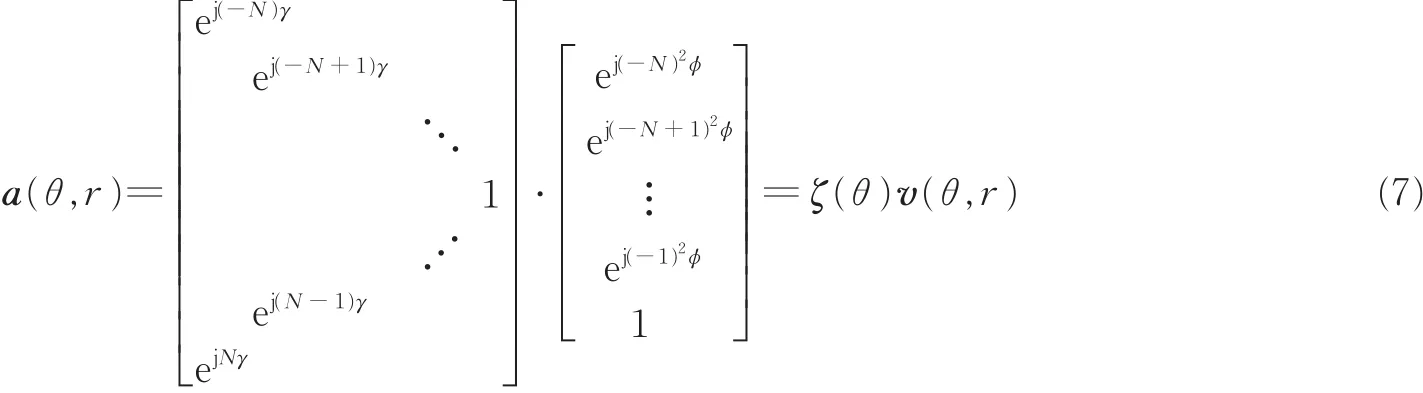
式中

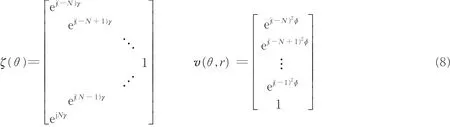
式中：ζ(θ)∈ C(2N+1)×(N+1)仅包含信源的角度信息，v(θ,r)∈ C(N+1)×1同时包含角度和距离信息。由式(8)可知 v(θ,r)≠ 0，故可将式(7)代入式(5)，得到

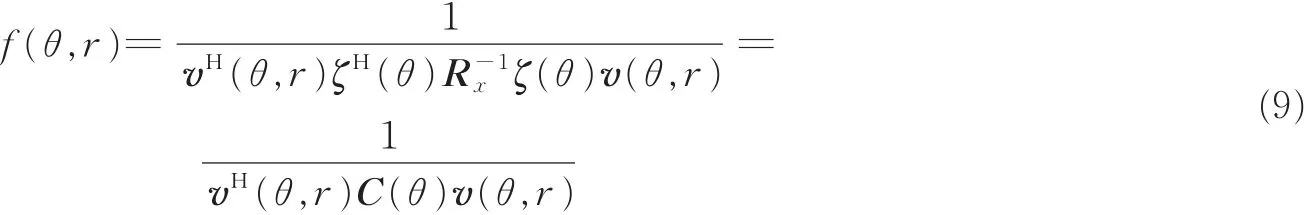
式中：C(θ)= ζH(θ )R-1xζ(θ)，可见 C(θ)∈ C(N+1)×(N+1)中只包含信源角度参数信息。又 v(θ,r) ≠ 0可知，C(θ )为非负定的共轭对称矩阵，因此 vH(θ,r)C(θ)v(θ,r)=0成立的充要条件为当且仅当 C(θ)为奇异矩阵。由假设条件可知，当K≤N时，噪声子空间Un的列秩不小于N+1，则可知C(θ)为满秩矩阵，只有当角度参数信息取到信源的实际位置时，矩阵C(θ)会降秩，即rank{C(θ)}＜N+1，此时C(θ)就会变成奇异矩阵，正交性成立。因此可以通过式(10)的一维谱峰搜索得到信源的DOA估计为

由式(10)得到信源的角度估计参数之后，将θ̂k依次逐个代入经典2D-Capon谱函数中，并构造式(11)中的距离搜索的谱函数，在距离上进行一维谱峰搜索，可得到距离参数的估计r̂k为

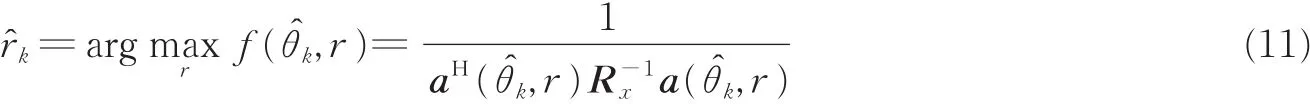
式中：距离的搜索范围r∈[0.62(D3/λ)1/22D2/λ]，k=1,…,K，由于需要将K个角度估计逐个代入，可知需要进行K次一维搜索。上述搜索过程能使得距离估计r̂k与角度估计θ̂k自动配对。

至此，已经完成了均匀线阵中近场信源基于降秩Capon算法的角度和距离参数的估计，该降秩Capon算法的主要步骤总结如下：

步骤1根据式(4)计算接收信号协方差矩阵Rx；

步骤2根据式(5)构造谱峰搜索函数，并按式(7)将导向矢量a(θ,r)拆分为a(θ,r)=ζ(θ)v(θ,r)，并构造C(θ)= ζH(θ)R̂-1xζ(θ)；

步骤3利用C(θ)，由式(10)构造关于角度信息的一维函数，通过角度搜索得到接收信号的DOA估计；

步骤4将得到的信源DOA估计结果逐个代入式(11)，然后再通过距离的一维谱峰搜索，得到与角度参数配对的距离估计。

3 算法分析

降秩Capon算法的复杂度主要包括：计算接收信号的协方差矩阵R̂x需要O{M2J}，求R̂-1x需要O{M3}，角度搜索需要 O{ngM(N+1)(M+N+1)}，K 次距离搜索 O{nlKM(M+1)}，因此总的复杂度为O{M3+M2J+ngM(N+1)(M+N-1)+nlKM(M+1)}；传统的经典2D-Capon算法的复杂度为 O{M3+M2J+ngnlM(N+1)(M+N+1)}。其中，ng=[π/2-(-π/2)]/Δg为角度空间的谱峰搜索次数；nl=[2D2/λ-0.62(D3/λ)1/2]/Δl为近场距离区间内的谱峰搜索次数，Δg和Δl为搜索步长；M为阵元个数；N=(M-1)/2；J为快拍数；K为信源个数。图2分别给出了本文所提出的降秩Capon算法与经典的2D-Capon算法在不同的阵元数和快拍数下的复杂度对比。由图2可以看出，相较于经典的2D-Capon算法，降秩Capon算法大大降低了计算的复杂度。

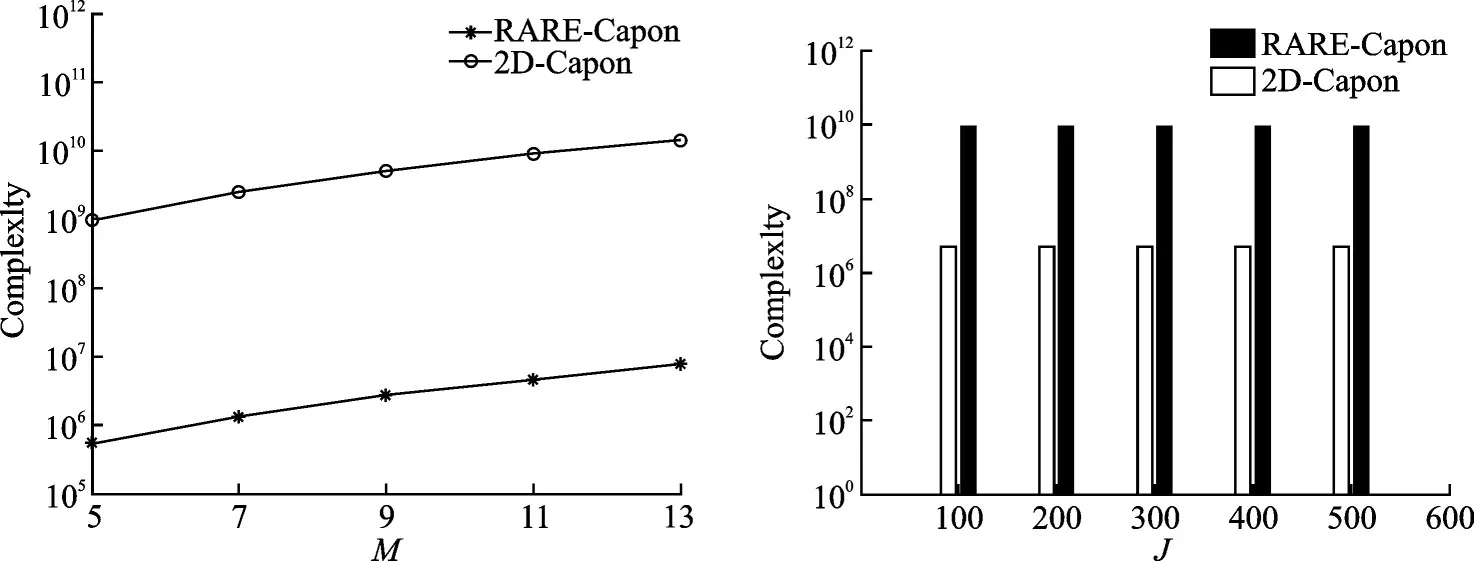
图2 算法复杂度对比图Fig.2 Complexity comparison of two algorithms

本文所提算法优点总结如下：

（1）该算法能够有效实现近场源角度与距离参数的联合估计，且参数自动配对；

（2）该算法避免二维谱峰搜索，相比较于经典的2D-Capon算法，大大降低了计算的复杂度；

（3）该算法的参数估计性能非常接近经典2D-Capon算法，具有较高的参数估计精度；

（4）该算法无需信源数估计。

4 仿真结果

本文采用蒙特卡洛实验仿真，仿真中假设有两个近场信号被阵列所接收，其角度和距离参数分别为(10°,0.3λ)和(40°,0.8λ)。M、K、J分别为阵列阵元数、信源数和接收信号快拍数。为了评估算法的参数估计性能，仿真实验次数为1 000次。角度和距离估计的求根均方误差(Root mean square error,RMSE)分别定义如下

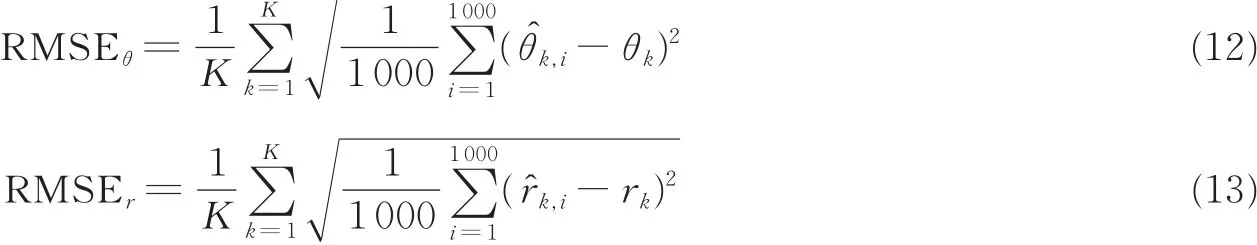
式中：θk和rk分别为第k个信源的角度和距离的实际值和分别为第i次实验中得到的第k个信源的角度和距离参数的估计值。

仿真1图3为本文算法在信噪比SNR=10 dB的情况下，角度和距离估计结果分布图。仿真中，阵元数M=9，信源数K=2，快拍数J=200。从图3可以看出本文算法可以有效用于近场信源的角度和距离参数估计。

仿真2图4和图5分别给出了本文算法在不同的快拍数下的角度和距离参数估计性能。仿真2中阵元数M=9，信源数K=2，分别设置信源数为J=100，J=200，J=300。由图中可以看到，随着快拍数的增大，本文算法角度和距离估计性能越来越好。

仿真3图6和图7分别给出了本文所提的RARE-Capon算法与传统的2D-Capon算法角度和距离参数估计性能对比图。仿真3中，考虑阵元数M=9，信源数K=2和快拍数J=200。从图6，7可以看出，本文中的RARE-Capon算法与经典2D-Capon算法参数估计性能非常接近。

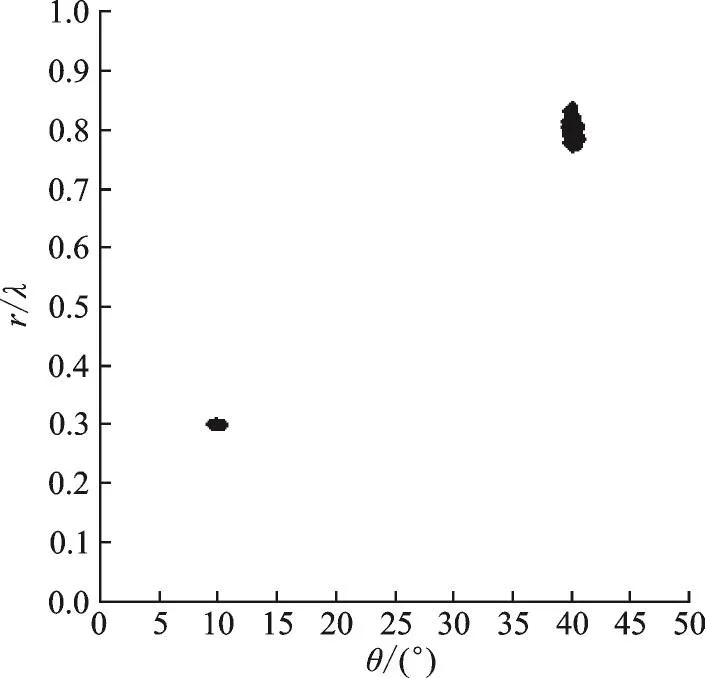
图3 角度和距离参数估计的散布图Fig.3 Angle and range estimation of the proposed algorithm

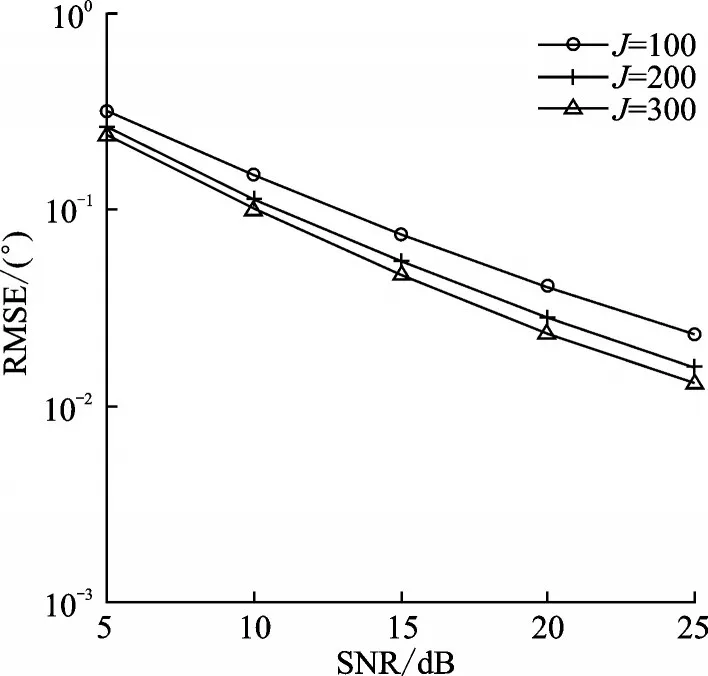
图4 角度的估计性能随快拍数变化情况Fig.4 Angle estimation performance versus different snapshots

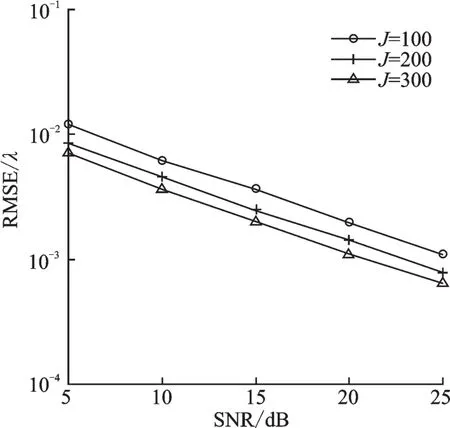
图5 距离的估计性能随快拍数变化情况Fig.5 Range estimation performance versus different snapshots

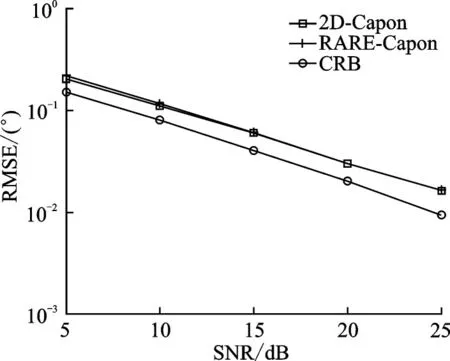
图6 角度估计性能对比Fig.6 Angle estimation performance comparison

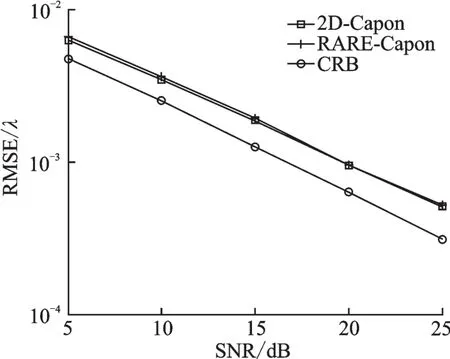
图7 距离估计性能对比Fig.7 Range estimation performance comparison

5 结束语

针对均匀线阵中近场信源的角度和距离参数联合估计问题，本文提出了一种降秩Capon算法。该算法无需信源数估计，且由于不需要进行二维谱峰搜素，其计算复杂度远远低于传统的2D-Capon算法。同时，该算法能够获得自动配对的角度和距离参数估计。仿真表明，其参数估计性能与经典的2D-Capon算法非常接近，且具有较高的参数估计精度。