一种基于全变分技术和Lp伪范数的椒盐噪声去除方法

许基隆，陈颖频

（闽南师范大学物理与信息工程学院，漳州，363000）

引 言

图像是信息获取、处理和理解过程中非常重要的来源，但由于采集、传输、存取过程中各种因素的影响，获取的图像通常是原图像的降质形式，例如，在数码相机成像过程中，较长的曝光时间会导致椒盐噪声[1-2]。椒盐噪声在概率分布上体现为：以一定的概率出现冲击扰动，以一定的概率出现零值扰动[3]。本文将从椒盐噪声的数学统计特性发出，以Lp伪范数对其加以刻画，并结合全变分技术消除椒盐噪声，提高图像恢复质量，从而为图像处理的后续工作服务。

椒盐噪声的去除方法有很多种，如：全变分（Total variation，TV）方法，TV方法分为各向异性全变分（Anisotropic total variation，ATV）[4-5]和各向同性全变分（Isotropy total variation，ITV）[5]；传统中值滤波方法(Median filtering，MF)[6]；数学形态 (Mathematical morphology，MM)方法[7]；脉冲耦合神经网络(Pulse coupled neural network，PCNN)[8]。其中，TV方法相比于MF、MM、PCNN去噪方法能更好地保护图像边缘。因此，近年来TV方法在图像解模糊、图像去噪、图像修复等方面得到了广泛的应用[9-12]。例如，陈颖频等将交叠组稀疏收缩技术引入广义全变分，提出一种具有高鲁棒性的图像恢复算法[13]。传统的TV方法一般以L1范数建模数据保真项，对噪声的稀疏性刻画能力并不理想。ATV方法相比于ITV方法有严重的阶梯效应。因此本文选择ITV去噪模型为改进对象。目前，基于ATV、ITV的椒盐噪声去除方法通常用L1范数来描述保真项。但是用L1范数做保真项的约束，对椒盐噪声的稀疏性刻画能力不足，所以本文用Lp伪范数代替L1范数，通过增加一个自由度来提高保真项对椒盐噪声的刻画能力[14]。

1 椒盐噪声去噪方法

1.1 基于ITV的椒盐去噪方法

基于ITV的椒盐去噪方法从去噪算法域的角度可总结成两种：一是空间域算法，二是频率域算法[15]。空间域又名像素域，在图像上以矩阵的形式存在。在空域上进行图像去噪处理时，难免要对图像矩阵进行列化操作，导致大型矩阵相乘，运算复杂度高。因此可以利用傅里叶变换把空间域中的图像转换到频率域中，在频域中进行处理后再反变换到空域，即频域算法[16]。基于椒盐噪声的特点，本文提出了一种频域去噪算法。

传统ITV椒盐噪声去噪模型为[5]

式中：f∈RN2×1为恢复图像的列化向量；g∈RN2×1表示被污染图像的列化向量表示数据保表示ITV正则项；分别表示横向差分矩阵和纵向差分矩阵；μ为保真项和ITV正则项的平衡参数；*表示二维卷积算子。

为减小矩阵规模、提高运算效率，本文将ITV模型改写为

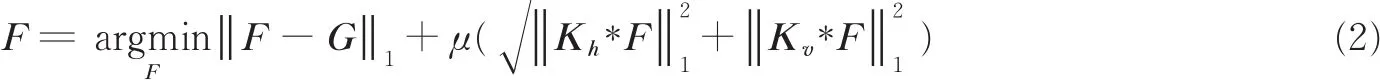
式中：F∈RN×N为原图像；G∈RN×N为被噪声污染的图像分别表示横向和纵向差分卷积核。

对比式（1,2）可知，式(1)中向量化形式的能量泛函涉及大型矩阵（∇h,∇v∈RN2×N2）运算的求逆运算，算法乘法复杂度为O((N2)3)，而其矩阵形式的能量泛函不存在大型矩阵，且卷积算子可以映射到频域后以点乘的形式进行运算，从而大大提高运算效率，算法复杂度仅为O(N2log2(N))。

1.2 Lp伪范数

Lp范数定义为伪范数定义为图1为不同Lp伪范数的等高线。

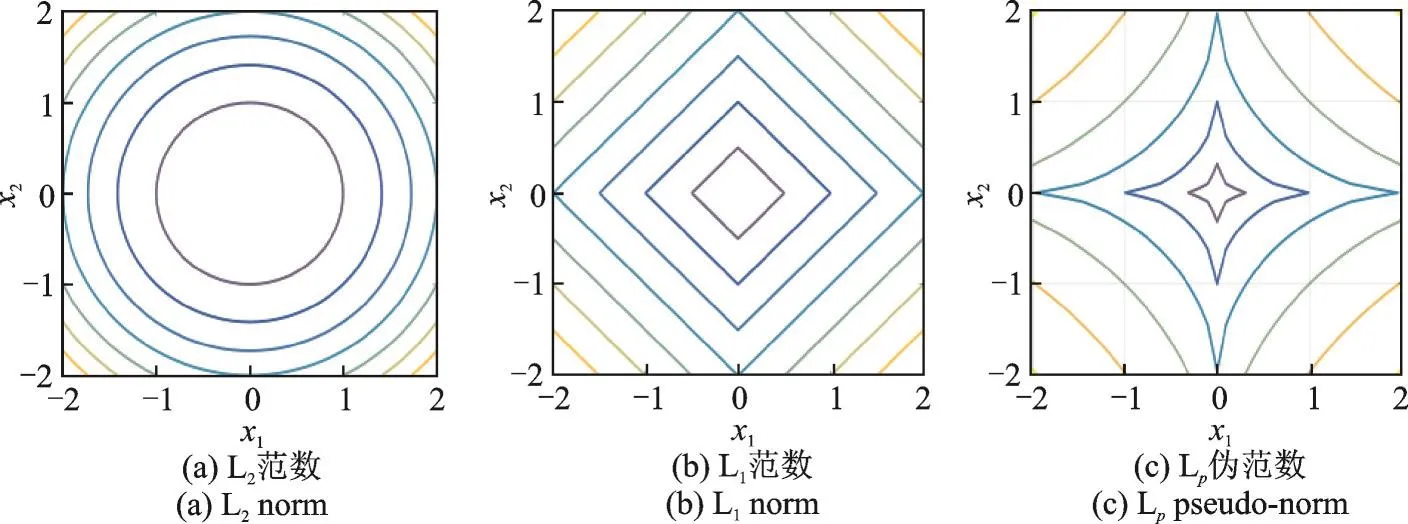
图1 各类范数等高线Fig.1 Contour line of different norms

传统的ITV椒盐去噪模型中用L1范数做保真项的约束，对椒盐噪声的稀疏性刻画能力不足。图2展示了不同范数的稀疏性刻画能力，其中f-g表示加在图像信号的噪声。显然，图2（c）中等高线上的点相比于图2（a，b）更高概率地逼近于坐标轴，因此用Lp伪范数能够诱导出更加稀疏的解，从而更好地描述椒盐噪声的稀疏特性。

图2 各类范数稀疏性Fig.2 Sparsity of different norms

鉴于Lp伪范数优良的稀疏刻画能力，本文对稀疏收缩算子加以改进，将基于L1范数的全变分图像恢复方法推广为基于Lp伪范数[14,17-21]的全变分图像恢复方法，用Lp伪范数代替L1范数，通过增加1个自由度来提高保真项对椒盐噪声的刻画能力。

2 基于Lp伪范数的ITV去噪方法

本文将Lp伪范数引入ITV模型，提出新的去噪模型如下

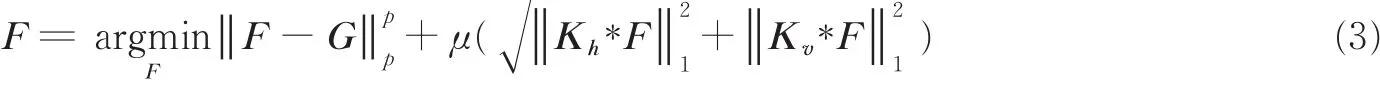
对比式(3)和式(2)可以发现，本文提出的模型相比于传统的ITV模型最大的差别在于将传统ITV的保真项伪范数加强对噪声数学统计特性的刻画，从而提高图像恢复的质量。

根据交替乘子迭代法框架，需要引入中间变量Z1=Kh*F，Z2=Kv*F，Z3=F-G，并引入对应的拉格朗日乘子Λ1，Λ2，Λ3。则增广拉格朗日目标函数为

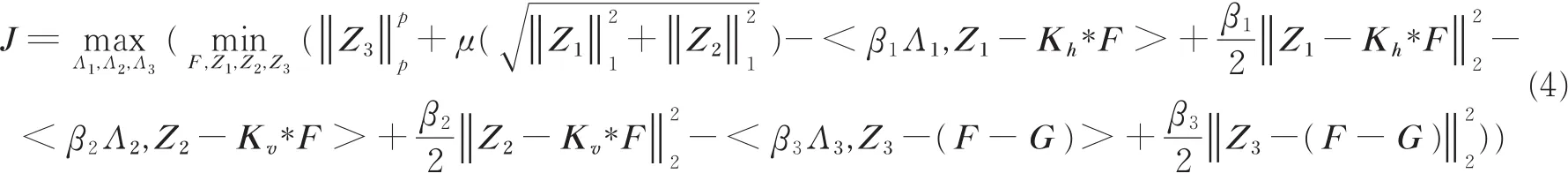
为求解目标函数，需要将每个变量的子问题求解出来。对于F子问题，有

由于引进的变量与F已经去耦合,则空域表达式为

利用卷积定理，频域表达式为

对式(8)Fˉ变量加以求导，并令导数为零，可以得到

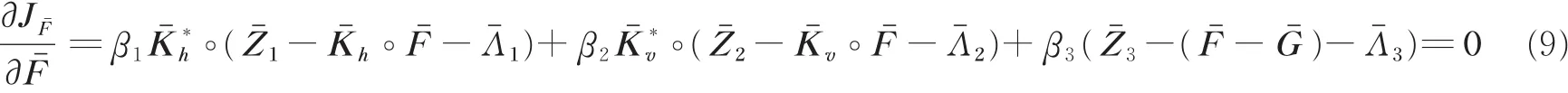
整理得

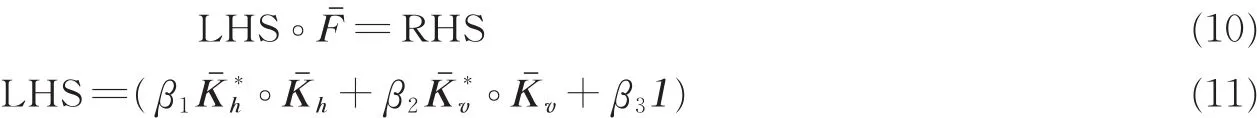
式中：1表示元素全为1的矩阵；RHS为

则有

式中：符号./表示点除操作；ℱ-1表示傅里叶逆变换算子。

对于Z1和Z2的子问题目标函数为

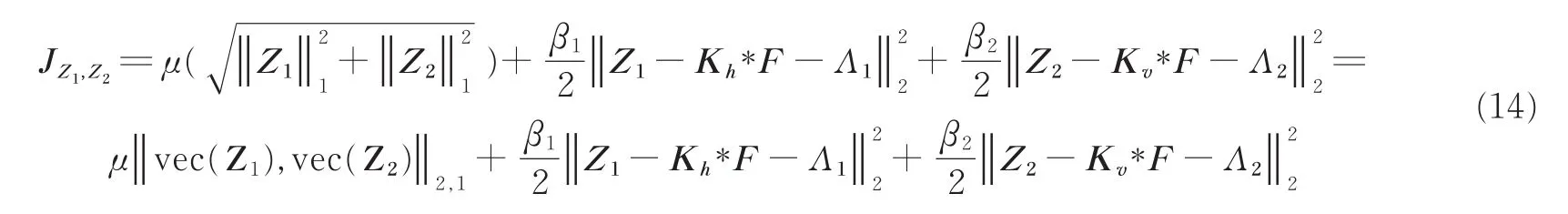
式中vec表示矩阵列化算子。令X=(vec(Kh*F+Λ1),vec(Kv*F+Λ2))，根据基于L21范数的收缩算子[22]有

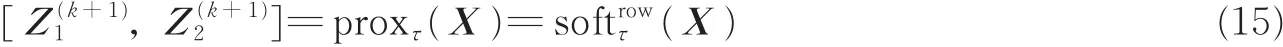
式中softrowτ为一个映射，定义如下

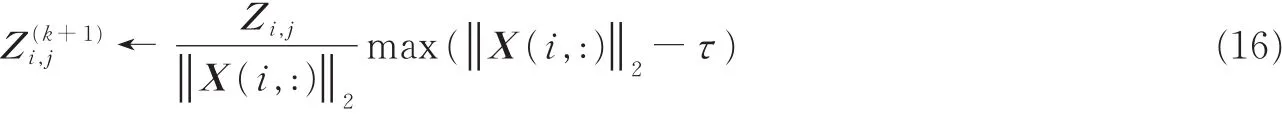
式中：Zi,j表示矩阵Z=(Z1，Z2)中第i行第j列的元素，Z为矩阵Z1和Z2的增广矩阵。这里假设X为Z的初始值，则X(i,：)表示矩阵X的第i行。

对于Z3子问题，目标函数为

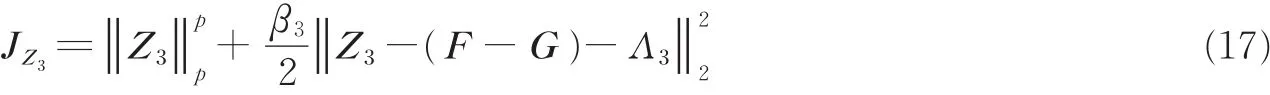
令A=F+ Λ3-G,τ=1/β3，根据 Lp伪范数收缩算子[18,23]，Z3的收缩规则为

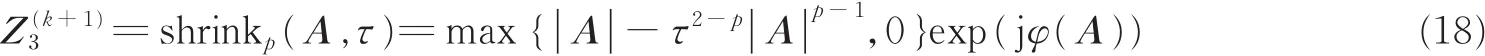
式中φ(A)表示A的相位。

对偶变量Λ1子问题为

利用梯度上升法，可以得到Λ1的更新规则为

式中δ＜1表示学习率。

对偶变量Λ2子问题为

利用梯度上升法，可以得到Λ2的更新规则为

对偶变量Λ3子问题为

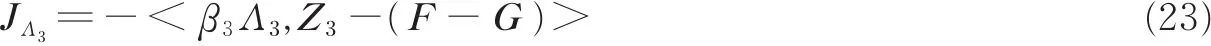
利用梯度上升法，可以得到Λ3的更新规则为

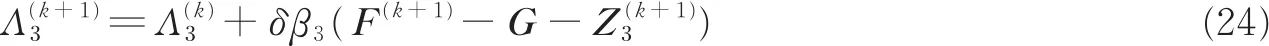
至此，所有子问题得到求解，本文提出算法ITV-Lp流程详见下面算法，其中设置tol为10-4。

算法 ITV-Lp

Input：观测图像G

Output：去噪图像F

Initialize：k=1,Zi=0,Λi=0(i=1,2,3),F(k)=0,μ，β1，β2，β3，δ，tol,p,E=1。

(1)While E＞tol,do

(2)利用式（13）更新F(k+1)；

(4)利用式（18）更新Z(k+1)3；

(5)利用式（20，21，24）更新 Λ(k+1)i(i=1,2,3)；

(6)k=k+1；

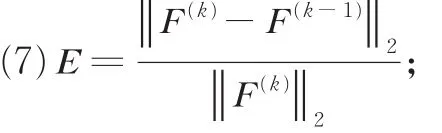
(8)End while

(9)Return F(k)as F

3 实验与分析

3.1 实验环境

为了证明本文所提出方法的优越性，本文针对4组图像进行实验，如图3所示，图像的大小为512像素×512像素。本文使用的椒盐噪声水平分别为10%，20%，50%。后续实验将本文方法与已有的方法进行对比，包括 ATV[5]，ITV[5]，MF[6]，MM[7]以及 PCNN[8]。

实验软硬件环境为：基于2.3 GHz的Inter CPU和8 GB的RAM硬件环境及Matlab软件开发环境。评价图像恢复治理的主要参数有：算法运算时间、峰值信噪比（Peak signal-to-noise ratio，PSNR）以及结构相似性信息（Structural similarity，SSIM）[24]。PSNR和SSIM的定义为

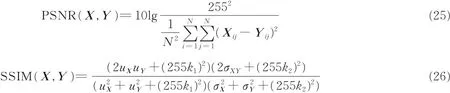
式中：X表示原始图像；Y表示恢复图像；μX和μY分别为图像X和Y的均值；和分别表示图像X和Y的方差；σXY为X和Y的协方差。本文令k1=0.01,k2=0.03。

3.2 实验结果

以图3中的图像为测试对象，加上不同水平的椒盐噪声，用上述6种方法进行图像去噪，结果如表1—4所示（最优指标用黑色粗体标出，表格中Time列为“-”时表示Matlab无法测出运算时间间隔）。从表中显示的结果可以看出，本文提出的去噪模型去噪效果最佳。

图3 测试图像Fig.3 Tested images

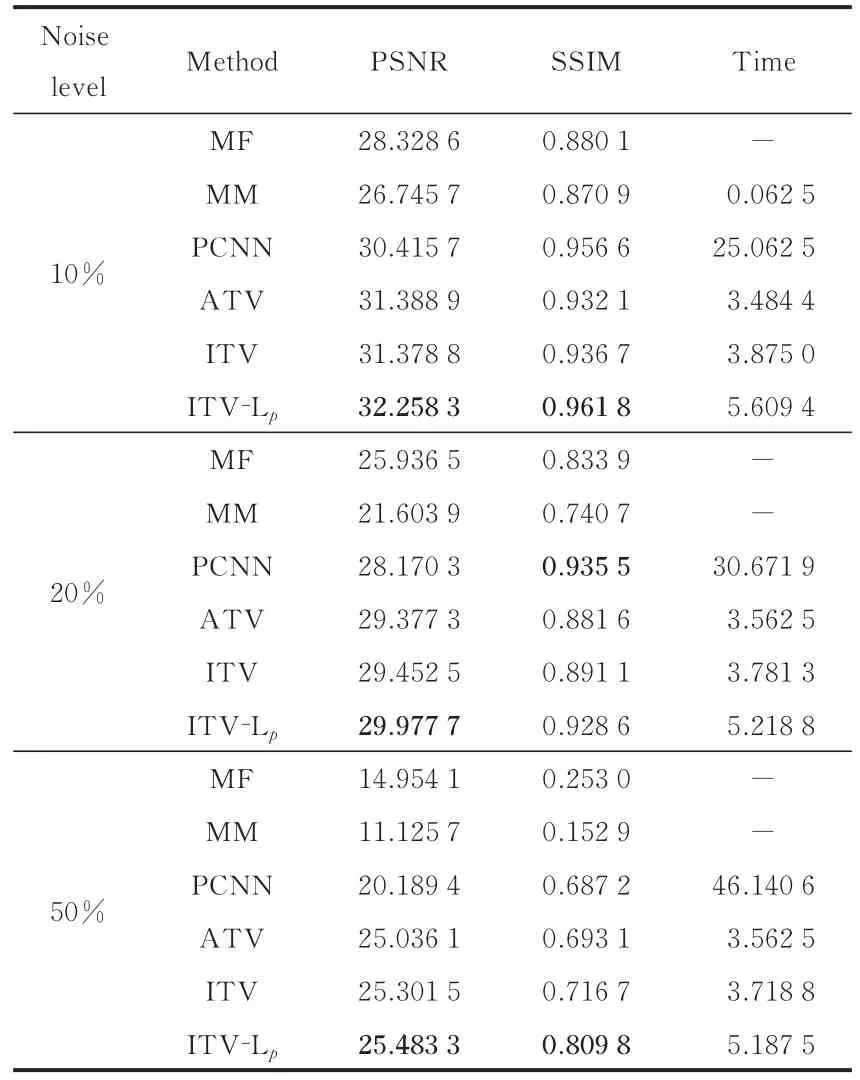
表1 不同方法关于Lena图像的去噪性能对比Table 1 Denoising performance of different methods with regard to Lena

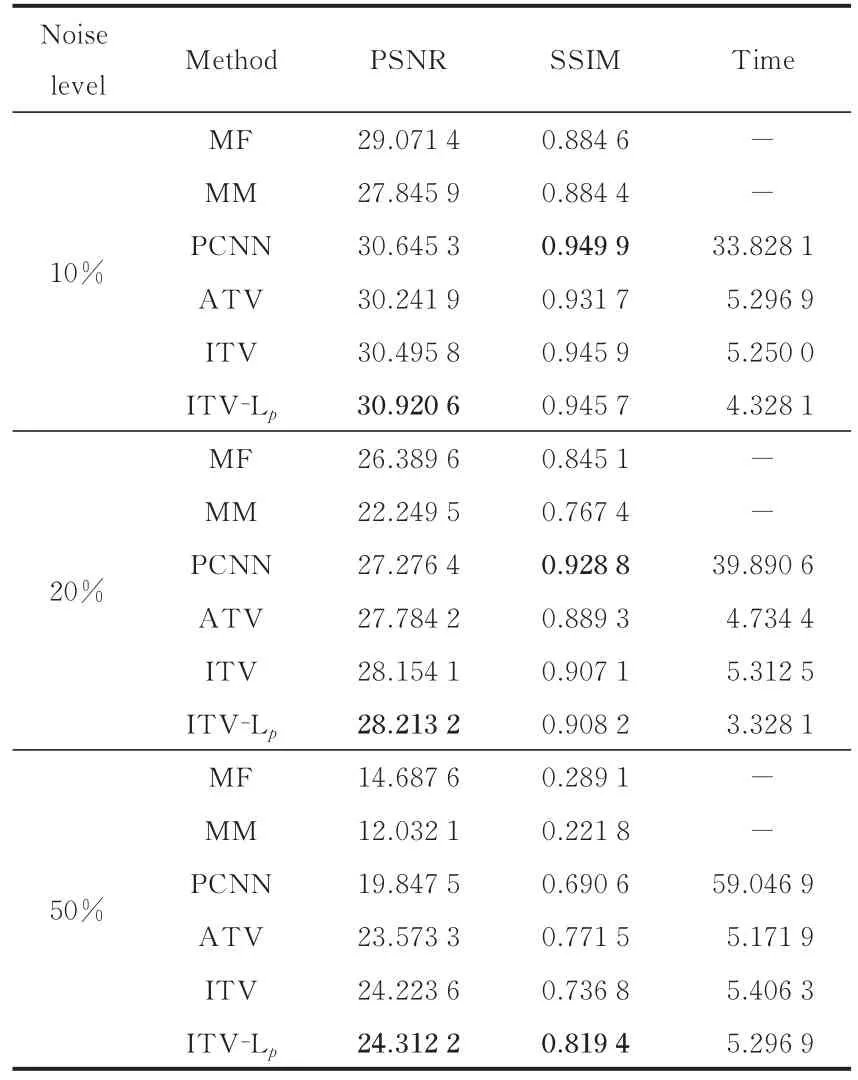
表2 不同方法关于Peppers图像的去噪性能对比Table 2 Denoising performance of different methods with regard to Peppers

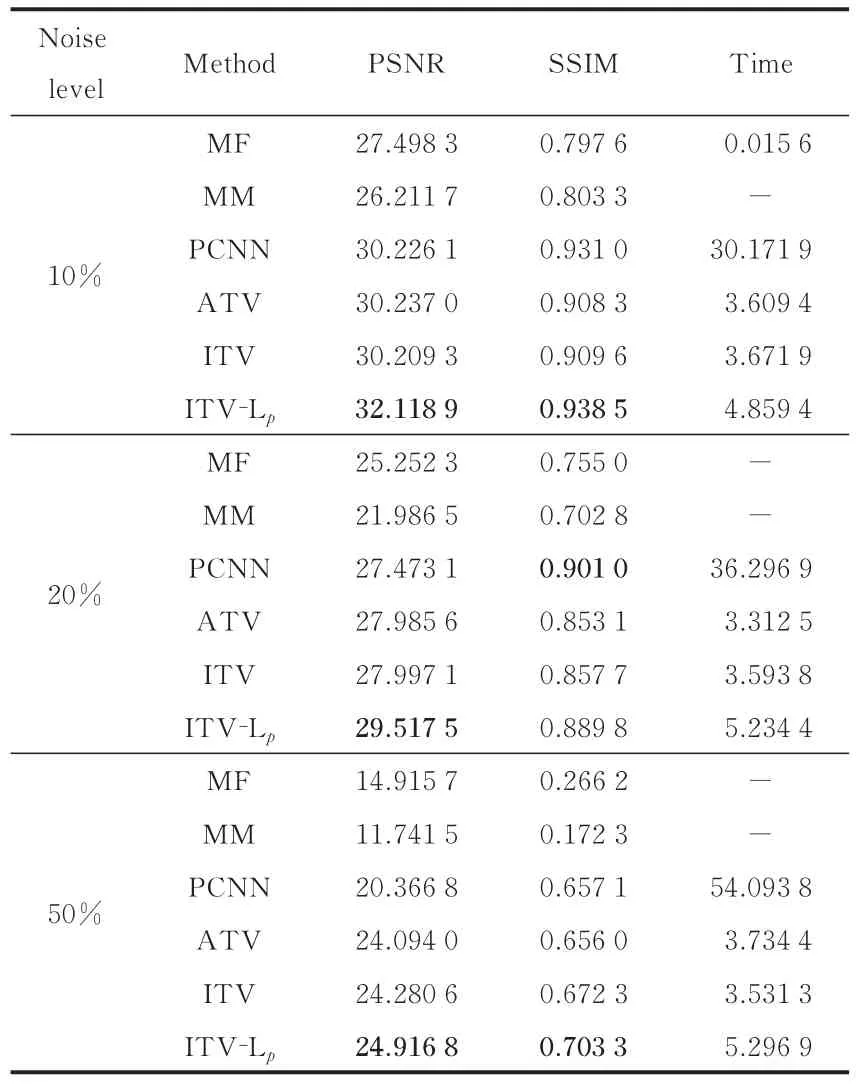
表3 不同方法关于Man图像的去噪性能对比Table 3 Denoising performance of different methods with regard to Man

表4 不同方法关于House图像的去噪性能对比Table 4 Denoising performance of different methods with regard to House

图4—7分别给出对大小为512像素×512像素的House和Lena图像分别加入噪声水平为10%和50%的椒盐噪声后，用6种算法恢复的图像和细节放大对比图。从视觉效果来看，本文方法去噪效果最好。

图4 不同算法对House图像恢复效果对比结果Fig.4 Comparison of recovered images of House by different methods

图5 不同算法对House细节图恢复效果对比结果Fig.5 Comparison of recovered images in detail of House by different methods

图6 不同算法对Lena图像恢复效果对比结果Fig.6 Comparison of recovered images of Lena by different methods

图7 不同算法对Lena细节图恢复效果对比结果Fig.7 Comparison of recovered images in detail of Lena by different methods

4 结束语

本文提出一种新的基于Lp伪范数和ITV的图像去噪方法ITV-Lp。为求解该去噪模型，ITV-Lp方法在ADMM算法中引入快速傅里叶变换，用点除运算代替空域算法，从而避免大型矩阵运算，提高运算效率。不仅如此，ITV-Lp方法还能避免占用大量内存的大型矩阵相乘运算。与ATV和ITV方法以及其他方法相比，ITV-Lp方法能获得最大的PSNR和SSIM值，这说明该方法不仅在误差方面，在结构相似性方面也能获得明显优于其他方法的图像结果。